数学とアートの世界-３種類の数学的な美しさについて-

ロマンティック

公開日

2020年6月9日

更新日

2020年6月9日

こんにちは！和からの講師兼切り絵アーティストの岡本です。

突然ですが、皆さんは数学好きですか？大多数の方が数学にあまりいい思い出がなく、「苦手」あるは「嫌い」であるのではないかと予想しています。しかし、今日はアートという視点から数学について熱く語っていこうと思います。この記事を読んで少しでも数学に興味を持っていただけると幸いです。

まず、私岡本は切り絵という独特な手法を用いて数学のアート作品を制作しています。今年（2020年）の２月には代官山で個展を開催いたしました。当時の展示について以前マスログで紹介させてもらったので興味のある方は是非ご覧ください。

切り絵展示会「紙で奏でるサイエンス―情緒―」のご紹介

こういった切り絵やアートの世界から数学を見つめなおす機会というのはなかなかなく、実際に世の中の大多数の方が数学のアートとしての一面を知らずに過ごしているように思います。そこで、芸術やアート、デザインといった視点から新しい数学の学び方があるのではないかと思い、数学とアートのセミナーを作成しました。

数学的デザイン超入門

セミナー開講に伴い、今回はアートとしての数学についてお話をしようと思います。より詳しい内容を知りたい方是非数学アート超入門セミナーにご参加ください！

※今回のマスログでは急に意味不明・未定義の専門用語が飛び出すことがありますが、「なんだか楽しそうだな」と思っていただき、気になる場合、是非セミナーで岡本に直接質問してみてください！（喜びます）

この記事の主な内容

１．アートの中の数学

数学というのは古来から芸術と深く結びついています。有名なところでいうと、ギリシャのパルテノン神殿に「黄金比」が使われているという話もあります（※諸説あります。神殿は屋根が崩れてしまい、今となっては全体の比を正確に確かめることができません）。そして実際に神殿の建設に携わった彫刻家のフェイディアスの頭文字から黄金比を表す記号「Φ（ファイ）」が使われています。

その他に数学とアートで有名なレオナルド・ダ・ヴィンチの「モナ・リザ」にも黄金比（レオナルドは「神聖比」と呼んでいます）が使われていますし、だまし絵で有名なマウリッツ・エッシャーは「双曲幾何学」を用いた「円の極限」という作品を発表しています。これは私たちの住む世界と違う、”平行線が交わることのある世界”でのタイル張り模様をモチーフにしています。とてつもない世界なんです。。。（岡本は大好物です）

エッシャーはイギリスの天才幾何学者コクセターのアドバイスを受け、こういった先駆的なアートを世に生みだしてきました。芸術家と数学者の見事なコラボレーションです。

クラインの壺栓抜き

近年では３Dプリンターやレーザーなどの科学技術の発達により、実現の難しかった３次元の幾何学模様を忠実に再現しオブジェとしての数学アートが次々と出現してきました。何を隠そう、岡本はこの流行りに乗り、「クラインの壺栓抜き」なるものをアメリカから取り寄せ、常に持ち歩いています。

もうすこし身近な例でいうと、公園や街の中でも数学的なデザインやアートを感じることができます。

例えば

東京ミッドタウン裏の公園

綺麗ですね！内側に見えるメリディアンとロンディチュードの曲線美がたまりません！

日本橋の箱崎ジャンクション（通称：ヤマタノオロチ）

クロソイド曲線の宝石箱や！

東京ジャーミィ

割とマイナーかもしれませんがイスラム教の立派なモスクが代々木にあります。イスラムアートの超緻密で超美しい対称性に言葉が出ません…。

そして極めつけは

フラクタルの屋根！

シェルピンスキーギャスケットの美しさはもちろんのこと、この屋根、数学的な構造から日除けとしての機能性を高めています。詳しい内容は以前のマスログをご覧ください

木陰とフラクタル

このように、私たちの日常には多くのデザインやアートがあふれてます。そしてその中の秩序として「数学」が見え隠れしているのです。続いては「数学の美しさ」の種類について簡単にご紹介いたします。

２．３種類の美しさ

数学には、大きく分けて３種類の美しさがあります。一つは「方法としての美しさ」、２つ目は「結論としての美しさ」、そして、３つ目は「経験としての美しさ」です。

①「方法としての美しさ」

次のような問題を考えてみましょう。

左の絡まった曲面を「切り貼りなし」で右のようにほどくことは可能でしょうか？それとも不可能でしょうか？ただし曲面は粘土のように伸縮自在だとします。

いかがでしょう。これ実は「可能」なんです！詳しい解法は次のマスログの後半に書いてますので「気になって眠れない。。。！」という方はぜ答え合わせをしてみてください。

ゲームの世界は丸いのか？～RPGから見るトポロジーの風景～

この問題の解法を脳内でイメージし、ほどけていく様子がなんともいえない美しさを醸し出します。これが「方法としての美しさ」です。

②「結論としての美しさ」

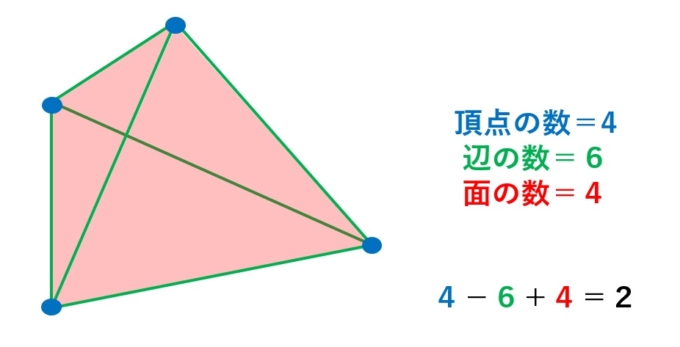
例えば「オイラーの多面体定理」が挙げられます。どんな多面体でも、（頂点の数）ー（辺の数）＋（面の数）＝２になるというなんとも不思議な定理です。試しに適当な多面体を描き、頂点と辺と面の個数を数えてみてください。上のように計算すると、必ず２になるはずです。０になったら、どこかに「穴が１つ」空いています。

このように結論が非常に一般的かつシンプルな定理は多くの数学者を魅了し、人類に発見される前から、人類が滅んだ後も、変わらずに輝き続けているのです。なんともロマンティックですね。

③「経験としての美しさ」

これは数学を実際に経験し、問題や理論を理解、解決、構築していくことで得られる発見や喜びそのものです。私自身、数学は山登りだと考えており、先の見えない前人未到の山を自分の足で登っていくことが数学の研究に当たります。ようやくの思いでたどり着いた山の頂から見下ろす景色は何とも爽快で美しいものではないでしょうか。経験としての本当の美しさは登った本人でないとなかなか感じられないかもれませんが、私たちは偉大な登山家たちが残した写真や登山記録を見ることはできるのです！

一言でまとめると「数学は大冒険である」。これに尽きます。

数学やその美しさを知ることで、世界は広がり、アートの世界も桁違いに広がります。

３．切り絵と数学

私自身、積極的にいままで触れてきた数学をモチーフとして取り入れ、切り絵の作品を創り上げてきました。最後に数学×切り絵の代表作品を詳しく解説いたします。

４次元に住む龍（2019）

これは４次元の球というものをモチーフにしました。私たちの住む３次元の世界の球というのはサーッカーボールのような丸い立体図形です。この３次元の球をスライスするとどうなるでしょうか？スライスすると断面に「円」が現れます。「円」とは”２次元の球”と考えることができます。まとめると「３次元の球をスライスすると２次元の球が断面に現れる」というものです。実はこの事実、次元を上げても同じことが言えます。つまりもし４次元の世界の球があったとします（当然４次元の世界はイメージすることができません）このとき「４次元の球をスライスすると３次元の球が断面に現れる」となります。断面が３次元の球なのです。これを表したのが作品です。いくつもの白い”３次元の球”が断面として並んでいます。３次元空間の中に第４の軸として「時間」を考えるならば、龍は過去・現在・未来を自由に行き来できる存在となります。そういった意味を込めて制作した作品です。

なお、この作品はアートブック「Energy2019」にて掲載されており、全国の書店でお買い求め可能です。

羅生門-rashomon-（2020）

こちらの世界と向こう側の世界はどのようにつながっているのか。普通に門をくぐれば「向こうの世界」に行けるわけではなく、この世とあの世をつなぐといわれる「羅生門」が特異点となり「モノドロミー」といわれる現象によって全く異なる空間に誘われているのではないか（ねじれが発生しているイメージ）、そんな意味を込めて作成しました。

なお、この作品は2020年10月にフランスのクロリュセ城で開催される「レオナルドダヴィンチ展」にて展示される予定です。

※クロリュセ城とはレオナルド・ダ・ヴィンチが晩年に過ごしたお城で、現在世界遺産となっています。フランスから出展の招待をいただき、10月に展示することが決まりました。