↓↓↓動画で見たい方はこちら↓↓↓

一次関数とは

一次関数とはy=ax+bのようにy=「一次（xのが最大でも1回かけられている）式」で書ける関数のことです。
xの一次式でなければ一次関数とは言わないので、xの2乗が式に入っていたりax+bのaが0であったりするときは1次関数とは呼びません。
例としては、y=5xやy=-3x+4などは一次関数です。

比例との違い

一次関数はy=axの形をしている比例の式に似ていますが式に定数項（ｘがかけられていない数）が入っているが特徴です。
この定数項は0でもよいので比例の式は一次関数となります。つまり、一次関数は比例の式の拡張（より広い意味）になっています。
逆に、y=-3x+4などはxが2倍,3倍,…になってもyが2倍,3倍,…になってはいないので比例の式ではありません。

一次関数のグラフ

一次関数のグラフについて見る前に、比例のグラフについての復習をしましょう。
例えば、比例の式y=5xであれば ,(x,y)が\((1,5),(2,10)(\frac{1}{2},\frac{5}{2})\)など無数の点を座標平面に打つことができます。この無数の点をすべてつなげたものがグラフであり、このグラフを比例のグラフと呼んだりしました。
また、原点を通り、かつ直線になる特徴があるのが比例のグラフでした。

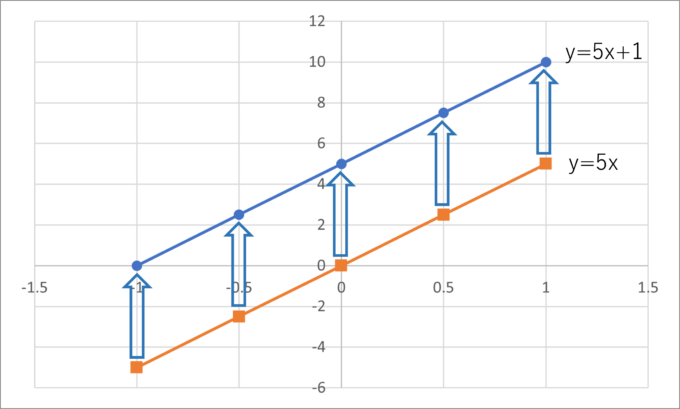
それに対して一次関数のグラフは、比例のグラフを“平行移動”させたグラフになります。
定数項を足したのが“平行移動”つまり、図形（直線）の形を変えずにグラフをずらすことに対応しているということです。

例えば、y=5x+5のグラフは下図のようにy=5x（同じ傾きのグラフ）を縦（y軸方向）に+5だけ平行移動したものとなります。

一次関数のメリット・デメリット

一次関数のメリットとしては、座標平面のほとんどの直線は一次関数を使って表すことができることです。このことから座標平面上の図形の接線（図形に接する直線）を一次関数で表すことができます。これはより高度な数学を学ぶときに役立ちます。

一次関数のデメリットとしては縦の（ｙ軸と平行な）直線は一次関数で表せないことです。この直線はx=〇の形で表せますが、y=の形ではあらせません。一方で、横の（x軸と平行な）直線は一次関数の傾きが0の関数として表すことができます。

一次関数の活用例

一次関数は高校以降で学ぶ微分の考え方の基礎になります。
色々な形の関数や図形を“大雑把に”とらえるときに使われるので、現代では統計学の活用やデータの処理などに使われています。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/尾崎>