↓↓↓動画で見たい方はこちら↓↓↓

時間と分の関係

時間（hour）から分に変換するには時間に\(60\)を掛けます。\(1\)時間は\(60\)分なので、\(2\)時間であれば\(120\)分です。これは、\(2\)時間⇒\(120\)分（\(2×60\)）としていますね。

\(1\)時間は\(60\)分であるという事実を用いて時間（hour）を分に変換するのですが、時間の表され方によっては計算をするときに混乱してしまいます。特に、時間が分数（ぶんすう）や小数で表現されている場合や〇時間△分を分に変換する場合は計算に一工夫が必要になります。

この記事では、時間(hour)から分への変換方法をパターン別に解説しています。

＊混乱を防ぐためこの記事では「〇時間」（例: \(1\)時間や\(12\)時間）を表す言葉「時間」は「時間（hour）」と表記しています。反対に一般的な意味での時間（例:集合時間や\(1\)秒、\(1\)分、\(1\)時間）は「時間」とそのまま表記しています。また、分数（ぶんすう）と分数（ふんすう）を区別するため、「分数（ぶんすう）」と表記しています。

※人気の社会人が算数を学び直す講座↓↓↓
いつか学び直したかった大人の算数講座-半年で6年分を理解する-

〇時間△分を分に変換する

はじめに、〇時間△分という風に表現された時間を分に直す方法を紹介します。例えば、\(２\)時間半であれば\(2\)時間（\(120\)分）に\(１\)時間の半分である\(30\)分\(（=60÷2）\)を足すので、\(150\)分（\(=120+30\)）と計算します。

ポイントは〇時間と△分を分けて考えるということです。△分はすでに分に変換されているので、最初に〇時間に\(60\)を掛けて分に変換します。その後、掛けて出た値に△分を足して答えを求めます。

例として\(3\)時間\(20\)分を考えると、はじめに\(3\)時間と\(20\)分を分けて考えます。\(3\)時間\(×60=180\)分になります。最後に\(20\)分を足して、合計で\(180+20=200\)分が答えとして得られます。

時間から分の変換（分数（ぶんすう）の場合）

分数（ぶんすう）で表された時間（hour）を分に直す際も時間を\(60\)で掛けることで計算ができます。このセクションでは、その理由とイメージについて解説します。

例えば、\(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\)などのキリが良い数字であれば分数（ぶんすう）から時間（hour）に変換する計算は簡単です。針のついた時計をイメージしてみましょう。

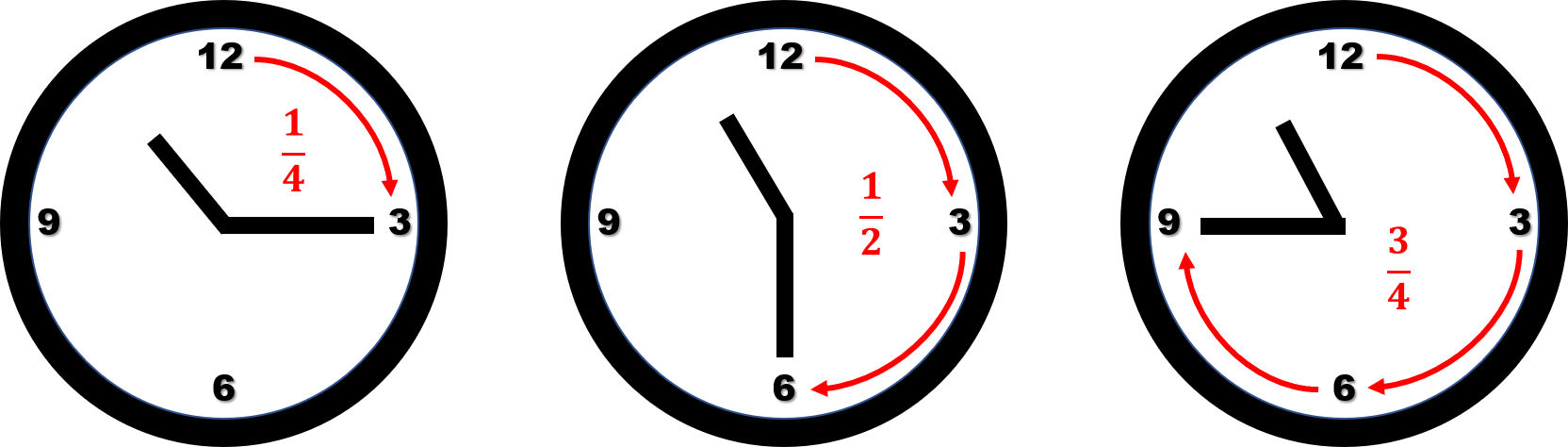
\(1\)時間で長針が一周すると考えられるため、\(\frac{1}{4}\)時間は円の\(\frac{1}{4}\)と考えることができます。\(\frac{1}{2}\)や\(\frac{3}{4}\)の場合も同様に考えることができます。

時計の長針を\(12\)の位置から\(\frac{1}{4}\)回すと\(15\)分の位置に移動します。\(\frac{1}{2}\)であれば\(30\)分、\(\frac{3}{4}\)であれば\(45\)分の\(1\)になります。このようにして、簡単な分数（ぶんすう）で表された時間であれば視覚的に時間（hour)から分に変換することができます。

簡単な分数（ぶんすう）であれば時計をイメージすることで簡単に計算ができますが、複雑な分数（ぶんすう）の場合は\(60\)を掛けて計算しなければなりません。\(1\)時間あたり\(60\)分であるということは分かっているので、\(\frac{1}{4}\)であれば\(\frac{1}{4}×60=15\)分と求めることができます。

\(\frac{1}{4}（時間）×\frac{60（分）}{1（時間）}=15\)分という風に（時間）という単位を打ち消して（分）の単位に直していると考えることもできます。

時間から分の変換（小数の場合）

時間（hour)から分への変換は時間が小数で表されている場合でも同様で、\(60\)を掛けることで求まります。

ただ、小数の掛け算は煩雑になりがちなので簡単な小数であれば分数（ぶんすう）に変換してから計算する方が望ましいです。例えば\(0.333…\)であれば\(\frac{1}{3}\)、\(0.25\)であれば\(\frac{1}{4}\)としてから\(60\)を掛けると計算量が少なく済みます。

例えば、\(0.875×60=52.5\)分と計算するよりも、
\(0.875×60=\frac{7}{8}×60=\frac{7×60}{8}=\frac{7×15}{2}=\frac{105}{2}=52.5\)分と計算すると、簡単な計算の組み合わせで答えが求まります。

時間と分数の活用

英語には時間を表すフレーズとして”half past 10”（10時から\(\frac{1}{2}\)）や”quarter until 6”（6時まで\(\frac{1}{4}\)）などの表現が存在していることをご存じでしょうか。\(\frac{1}{2}\)は\(30\)分なので、最初の例は10時30分を表します。また、\(\frac{1}{4}\)は\(15\)分なので\(2\)番目の例は5時45分を表します。時間から分をすぐに変換できるとこのような表現にも慣れ親しむことができます。また、時間から分に変換することによって分かりやすくなることもあるのでこの機会にぜひ習得してみましょう。
社会人が算数を学び直す講座に興味がある方は、いつか学び直したかった大人の算数講座-半年で6年分を理解する-にぜひお越しください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/須藤>