「極座標ってなんのためにあるの?」— 場所を特定するための座標の違い
公開日
2025年2月19日
更新日
2025年2月13日

みなさんこんにちは!和からの数学講師の岡﨑です。
和からでは、学びに来る皆様のさまざまな「分からない」に答えるべく日々授業を行っています。
今回はその中の一つ、極座標についての話をご紹介しましょう。
この記事の主な内容
1.「極座標がなんのためにあるのかわかりません!」
Aさん:先生、極座標がどうしても理解できません!
先生:どこがわからないのですか?
Aさん:どこがというか、そもそも極座標というものがなんなのか、なんのためにあるのかが教科書を読んでもよくわからないんです。
Aさん:普通の直交座標(デカルト座標)ならイメージできるんですよ。たとえば、ある点の位置を『横に3、縦に2』みたいに表すのはわかります。
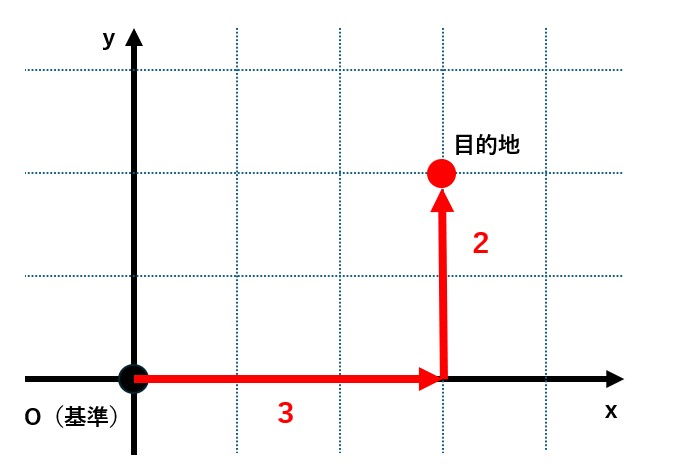
先生:緯度と経度で地球上の位置を示したりする際など、直交座標の考え方は比較的なじみやすいかもしれませんね。
Aさん:そうなんです。でも、極座標になったとたんに偏角とか動径とか、挙句の果てにsin(サイン)とかcos(コサイン)とか、何のために何の計算をしているのかさっぱり分からなくなってしまいます!
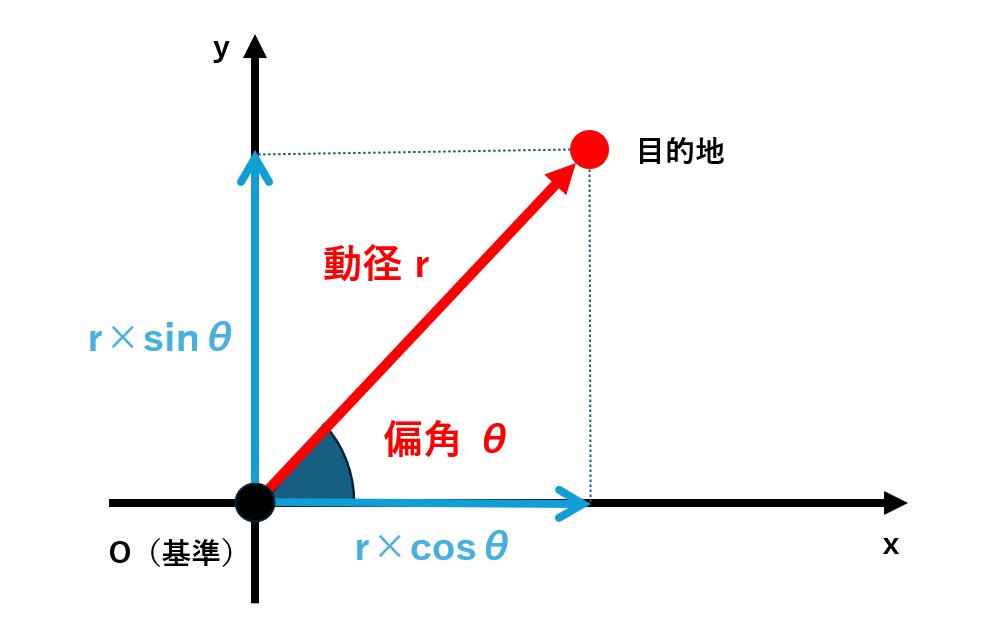
先生:なるほど。それでは、日常の場面に置き換えて考えてみましょう。
2.直交座標と極座標の違い
先生:たとえば、Aさんは遊園地に友人と遊びに来ていて、観覧車の前で順番待ちをしているとします。
Aさん:楽しみですね!
先生:そうですね。そのとき、観覧車のゴンドラの一つにたまたま別の友人が先に乗っていることに気づいたとしましょう。
Aさん:出かけた先で偶然友達に出くわすと、誰かに話したくなりますね!
先生:そこで隣にいる友人に気づいたことを伝えるときに、どのようにゴンドラの位置を説明しますか?
Aさん:『あれ!』と指をさします!
先生:(笑)。もちろん指をさしても良いですが、今回は飲み物と荷物を持っていて、両手がふさがってしまっているため言葉で伝える方法を考えてみることにしましょう。
Aさん:それなら…『右側の、地上から20メートルくらいのところ!』とかですか?でも見た目で距離を判断するのは難しいし、うまく伝わらなさそう…
先生:そうですね。それでもある程度伝わるかもしれませんが、もっと簡単な伝え方があります。
先生:例えば、『時計でいうと1時の方向にいるよ!』と言ったら、どうでしょうか?
Aさん:あっ、それなら右上あたり、特に真上に近いところにいることがすぐにわかるので、直感的ですね!
先生:実はこれが極座標の考え方です。
Aさん:なるほど……!直交座標は縦と横に移動する量で位置を示すのに対して、極座標は方向を使って位置を示すのですね!
先生:その通りです。極座標では基準となる中心、つまり今回は観覧車の中心からの距離を動径、方向を偏角と呼びます。直交座標も極座標もどちらも場所を特定するための方法ですが、考え方が違うのです。
3.極座標を使う利点
先生:では、なぜわざわざ極座標を使うのでしょうか?
Aさん:確かに、直交座標で表せなくもないなら、極座標を使う意味はあるのでしょうか?
先生:もちろんあります!極座標が特に便利な場面を考えてみましょう。
先生:観覧車はグルグル回りますから、ゴンドラの位置は時間とともに変わります。直交座標では動くたびに『高さと横の位置』を考えないといけませんが、極座標なら『角度が何度変わったか』だけで表せます。
Aさん:たしかに、観覧車は常に円を描くように動くので、角度がわかれば位置がわかるのですね!『1時の方向、2時の方向、3時の方向…』と時計の針と同じように場所がすぐに説明できます。
先生:その通りです。回転運動や円の形を持つ現象を考えるとき、極座標はとても便利なのです。車のタイヤや扇風機など、回転するものは身の回りにもたくさんあります。
Aさん:なるほど!確かに、こうした回転の問題を直交座標で考えると面倒そうですね。
4.極座標と複素数
先生:もう一つ、極座標が役立つ場面を紹介しましょう。
Aさん:どんな場面ですか?
先生:複素数の計算を考えるときです。
Aさん:そう!極座標の話が出てきたのは、ちょうど複素数について勉強しているときでした!
先生:では、これも日常の例に置き換えてみましょう。
先生:例えば、Aさんがカメラのズーム機能を使って、最初に2倍に拡大したとします。そして、そのあともう一度1.5倍に拡大したら、元の大きさの何倍になりますか?
Aさん:えっと、最初に2倍して、次に1.5倍だから……3倍ですね!
先生:その通りです。倍率の計算は掛け算するだけで求められます。
Aさん:たしかに、これは簡単ですね。
先生:実は、複素数の掛け算も同じなのです。極座標で表すと、複素数どうしを掛け算したときの大きさ(動径、複素数の場合は絶対値と呼びます)はそれぞれの大きさをかけるだけで求まります。
Aさん:なるほど!それなら直感的にわかりやすいですね。
先生:さらに、方向(偏角)についても同じことが言えます。たとえば、Aさんが金庫のダイアルを右に30°回転回して、さらに45°回転回したら、合計で何度回転したことになりますか?
Aさん:それは簡単ですね。30° + 45° で 75° です!
先生:その通りです。角度を足すだけで求められます。極座標で複素数を扱うと、この計算と同じことができるのです。
Aさん:それはとても便利ですね!直交座標で計算するより簡単かもしれません。
先生:そうですね。だから、複素数の計算をするときは、極座標を使うと楽になる場合が多いのです。
5.まとめ
Aさん:つまり、
Aさん:ということですね!極座標を使う理由がよくわかりました!
先生:数学では、何を扱うか、どんな計算をするかに応じて適切な座標を選ぶことが重要です。
6.さいごに
極座標などの一見すると『なんのためにあるんだろう?』というものも、ひも解くと使われるようになった理由と経緯があるものが多いです。
仕組みが分かると難しそうな数学の問題も簡単に解けるようになり、何より数学を通じて色々なことを考えることが楽しめるようになってきます。
和からでは、こうした高校や大学以上の数学を個別授業形式で学習することができます。お客様に合った授業が実現できるように柔軟に対応することができますので、個別授業に興味のある方はぜひ一度無料カウンセリングにご参加ください!
複素数について理解を深めるために書籍で勉強したい方は、結城浩先生の 数学ガールの秘密ノートシリーズ:複素数の広がりで分かりやすく解説されていますのでぜひご覧になってみてください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡﨑 凌>














