暗記嫌いのための速度算～速さ・時間・道のりの関係～

公開日

2020年6月28日

更新日

2020年6月28日

こんにちは、和からの池下です。

突然ですが…私は昔から大の暗記嫌い（苦手）です！
英単語や歴史の年号・人物名はもちろん、算数の九九も、最後の最後まで半ベソで居残りテストを受けていたタイプでした…。

算数や数学では、九九以外にも「公式を暗記してテストを乗り越えてた」というようなお話しを、お客様からよくお聞きします。
その中でも「当時暗記してたよねあるある」でよく話題にあがるのが「速さの計算」です。
なんだっけ？という方も、「み・は・じ」とか「き・は・じ」と言えばボンヤリと思い出すでしょうか。
小学校では「速さ・時間・道のり」という単元で習いますし、就職や転職に使われるSPI試験でも「速度算」という分野で出題されています。
そんなこともあり、最近は特に社会人が算数を学び直す講座も人気です。
いつか学び直したかった大人の算数講座-半年で6年分を理解する-

そんな中で、勉強の方法や理解のプロセスは、その人の得意不得意/好き嫌いによってそれぞれ異なると思うのですが、今回は私と同じように“暗記嫌い”で苦戦したことのある同志の皆さまに向けて
「公式を暗記しなくてもだいじょーぶ！」な速度算についてお話しさせていただければと思います！

この記事の主な内容

まずは速さ・時間・道のりの公式を思い出そう

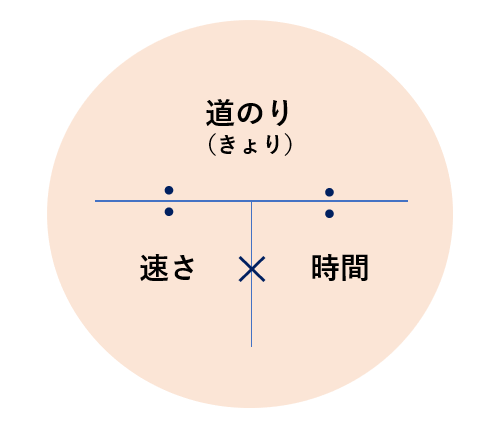「あー、なんかこんなのやったなぁ」と思われた方もいらっしゃるでしょう。
これは
【速さ】を知りたければ　「道のり ÷ 時間」
【道のり】を知りたければ「速さ × 時間」
【時間】を知りたければ　「道のり ÷ 速さ」
で計算すれば答えが出せるよ、という数量の関係をマルっと一つの図で表したもので、これを暗記しまえば、正直テストに必要な計算は事足りるかもしれません。
が、今日のテーマは暗記嫌いのための速度算！！！ですので、さっそく「どうしてこういう関係になるの？」について考えていきましょう。

そもそも「速さ」ってなに？

「速いなぁ」と感じるものにも色々ありますよね。
新幹線や飛行機、ロケットなどの乗り物はもちろん、動物だとチーター、人間ならウサイン・ボルト…。

さて、ここで想像してみてください。
あなたは新幹線に乗っています。
ふと窓の外を眺めるとなんとそこには並走するチーターの姿が…！
しかしスピードは新幹線の方が速いので、チーターはどんどん後ろへ遠ざかっていきます…。

さあこの時、みなさんはチーターのことを「速いなぁ」と思うでしょうか？
恐らく直感的に「速！」とはならないと思います。

つまり何が言いたいかというと、
何と比べるか（何を基準にするか）によって、同じ速度でも「チーターの速さの評価が変わってしまう、ということです。

チーター　⇔　私「速！」
チーター　⇔　新幹線「遅いな…」
と、こんなふうに。

ただ、私たちが普段「速さ」を扱うにあたり、人によって基準が違う＝評価もバラバラというのは、収拾がつかず困ってしまいますよね。

なので私たちは主に「一定時間あたりに進んだ距離」を共通のモノサシとして、速さを表すことにしています。

速さを
1時間あたりに進んだ距離で表すなら「時速」
1分間あたりに進んだ距離で表すなら「分速」
1秒間あたりに進んだ距離で表すなら「秒速」
という感じですね。
これで速さという曖昧なものを、みんなと「共通の基準」で、「どれくらい速いか」を具体的な数値で表すことができるようになるのです！（便利！）

[例]
Aさんは1時間あたり８km走った（時速8km）
Bさんは1時間あたり６km走った（時速6km）
⇒1時間あたりに進む距離が2km多いから、Aさんの方が速いね！

「速さ・時間・道のり」の三角関係

前置きが長くなりましたが、ここから「速さ・時間・道のりの公式」について具体的に考えていきましょう。
今日のテーマである“暗記しない”コツは数式に「意味を与えて考えてみる」こと、です。

◆【速さ】を求めるための　「道のり ÷ 時間」
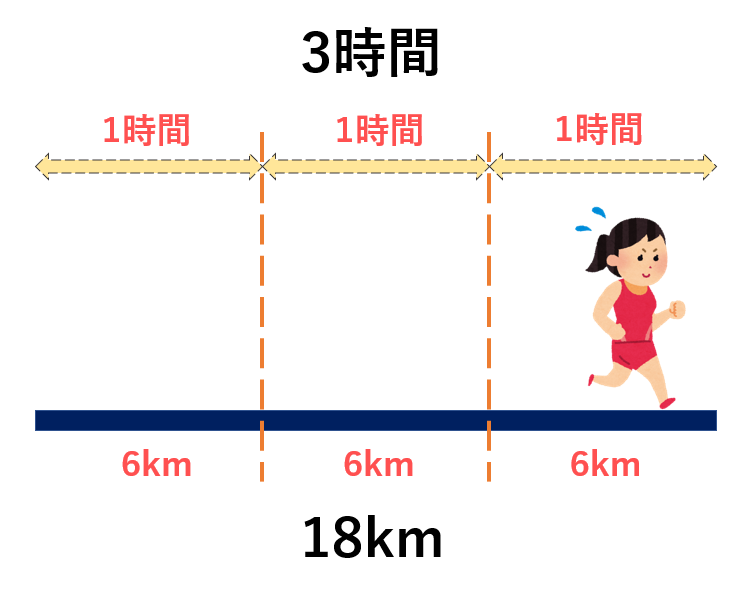
■例題①■ 3時間で18km走った場合の速さは？
まずは速さを求める公式です。
公式どおりに計算すれば「道のり÷時間」で
18(km) ÷ 3(時間) = 6(km/時)
と簡単に計算はできますが、
ではこの計算の意味するところはなんでしょう？

■考え方■
これは、みなさんが飲み会で割り勘する時と同じ考え方で解決できます。
4人でお会計が20,000円なら“一人当たり○円”を出すために 20000÷4をしますよね？
それと同じように合計18km走った時の“1時間あたり〇km”を出すための割り算と考えるのです。
（前述したとおり、“1時間あたり〇km”というのは速さを表す【時速】のことです）

◆【道のり】を求めるための　「速さ×時間」
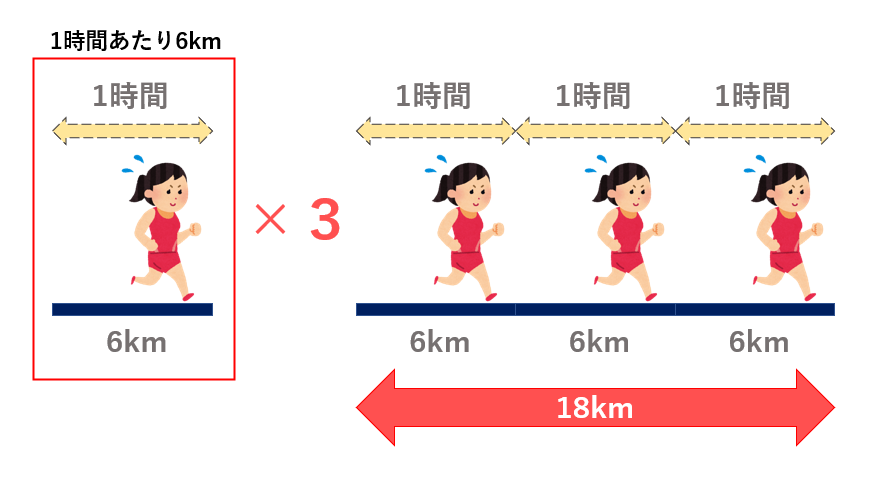
■例題②■　時速6kmで3時間走った場合の道のりは？
これも公式どおりであれば「速さ×時間」で
6(km/時) × 3(時間) = 18(km)
となりますね。

■考え方■
この掛け算は、よくあるお買い物する時の計算と同じです。
「1枚あたり8,000円のライブのチケット、3枚買ったらいくらになるかな？」と同じように
「1時間当たり6km走れるのであれば、3時間走ったら何kmになるかな？」という具合です。

◆【時間】を求めるための　「道のり÷速さ」
■例題③■　18kmの道のりを時速6kmで走った時にかかる時間は？
最後の公式です。
時間を求める場合、公式では「道のり÷速さ」となるので
18(km) ÷ 6(km/時) = 3(時間)
となりますね。

■考え方■
ここでは、①と違う割り算の意味で考えます。
みなさんのお財布に1万円札が一枚入っているとして「500円のガチャガチャ何回回せるだろう？」って考える時、割り算をしませんか？
「500円を何回積み重ねたら10,000円になるか」つまり「10,000円の中に500円が何セットあるか」を数える時に、割り算を使うのです。
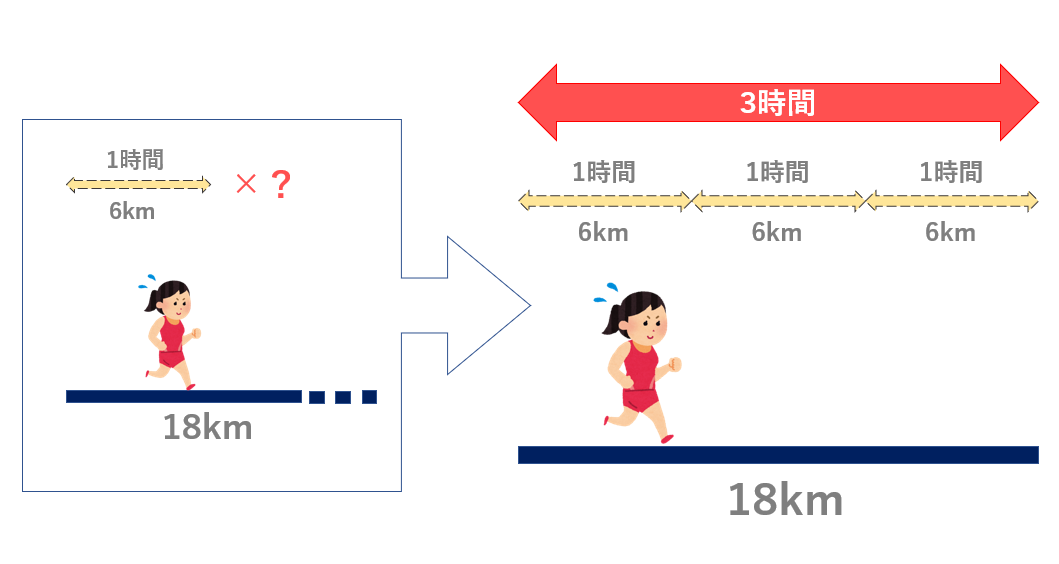
それと同様に考えて、「18km走りきるのに6km(1時間)が何セットあるだろう？」
これを計算式に置き換えると18÷6=3になる、という訳です。