倍数とは・約数とは【算数からやさしく解説】

算数・物理・数学トピック

公開日

2022年3月24日

更新日

2024年8月4日

↓↓↓動画で見たい方はこちら↓↓↓

この記事の主な内容

倍数、約数とは

倍数（ばいすう）とは、ある数を整数倍した数のことを言い、（正の）約数（やくすう）とはある整数を割り切る正の整数のことを言います。
例えば、3の倍数とは整数を3倍した数、つまり、3（整数）の形をした数のことなので、…,-6,-3,0,3,6,…のような数が3の倍数となります。また、約数はある整数を割り切る正の整数のことなので、6の約数は1～6の中にあります。したがって、1から順番に6を割り切れるか考えていけば、1,2,3,6が6の約数とわかります。
この例以外にも様々な数について倍数と約数を考えると、どんな整数の倍数にも必ず0が含まれていることや、約数には必ず1と自分自身が含まれていること、ある約数で元の数を割ったものが別の約数になることなどがわかると思います。

素数について

約数の求め方を紹介する前に素数について少し説明したいと思います。
どんな整数でも必ず約数に1と自分自身を含みますが、逆に、1以外の整数で1と自分自身以外の約数を持たない数を素数（そすう）と呼びます。2,3,5,7,11,13,…などが素数となる数です。
整数の重要な性質として、「どんな整数でも必ず素数の積（掛け算）で表せる」というものがあります。この整数を素数の積で表すことを素因数分解（そいんすうぶんかい）といいます。
例えば、30の素因数分解は2×3×5のように素数2,3,5を使った形で表されます。

約数の求め方

倍数は整数をかけるだけで求めることができるので、約数の求め方を2つ紹介したいと思います。
1つ目は、例で行ったように1～自分自身の中で割り切れる整数を一つ一つ調べていく方法です。この方法は小さい数などでは簡単に行うことができますが、扱う数が大きくなると難しくなってしまいます。また、約数が1つわかると元の数をその数で割ったものも約数になることを使うと労力が半分ですみます。基本的にはこちらの求め方ができれば十分です。
2つ目は、素因数分解を用いる方法です。
それでは素因数分解を用いて12の約数を求めてみたいと思います。12を素因数分解すると\(2^2×3\)です。
ここで約数の見方を変えると、12の約数とは12を割り切る正の整数のことなので、
\begin{align*}
\frac{12}{約数}=（整数）
\end{align*}
となるものです。なので、12の約数は約分しても分母に整数が残ってしまうことから、素因数分解したときに\(2^3や5,7\)などは現れないことがわかります。
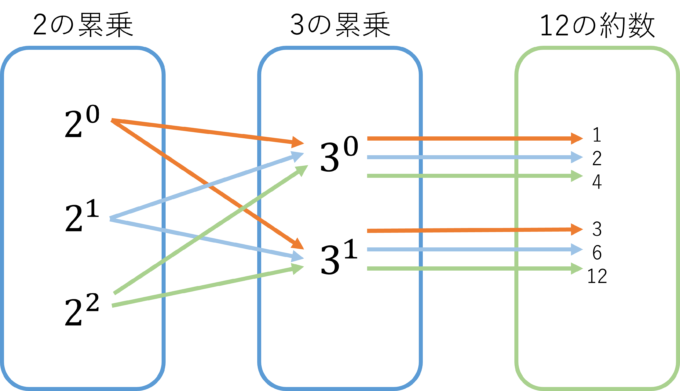
したがって、下図のように12の約数は\(2^0,2^1,2^2と3^0,3^1\)の組み合わせで求めることができ、1,2,3,4,6,12とわかります。

倍数、約数のメリットとデメリット

倍数、約数は整数の掛け算や割り算に関する基礎的なものなので慣れればお金に関することなど、日常生活で広く活用できます。しかし、これらは小・中学校で習う基礎的なものではありますが、素数との関連や約数の個数、約数の総和（約数をすべて足し合わせた値）など現代で研究されているような未解決なものなどを多く含みます。