はじめに

大人のための数学教室和(なごみ)の講師の松中です。最近印象に残った授業シリーズとして不定期に授業の内容を紹介していきたいと思います。今回紹介したいのはポアソン分布の期待値に関してです。

なおこちらの記事の内容は動画でも解説しています。

モーメント母関数を用いたポアソン分布の期待値の導出

まずポアソン分に関して簡単に紹介します。例えば、過去の経験から1時間に平均$\lambda$回のいたずら電話がかかってくることがわかっている電話があったとします。ある1時間の間にその電話にかかってくるいたずら電話の回数が従う分布がポアソン分布になります。

このように単位時間に平均$\lambda$回発生する事象があるとき、ある単位時間にその事象が発生する回数を$X$とすると、$X$はポアソン分布に従います。ポアソン分布に従う確率変数$X$が各値をとる確率は次の式で与えられます。

$$P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}$$

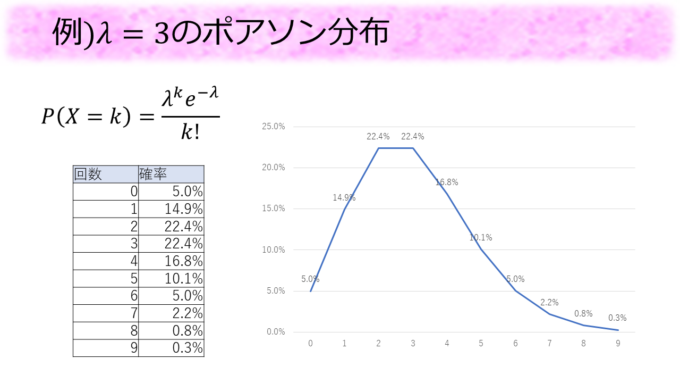
具体的にポアソン分布に従う確率変数$X$が各値をとる確率を見てみましょう。$\lambda$を$3$とすると、各確率は上の表のように計算できます。グラフを書いてみるとたしかに$X$が$3$周りの値をとる確率が大きくなっていることが確認できます。$\lambda$を$3$より大きくすると、このグラフの山は右の方に動いていきます。

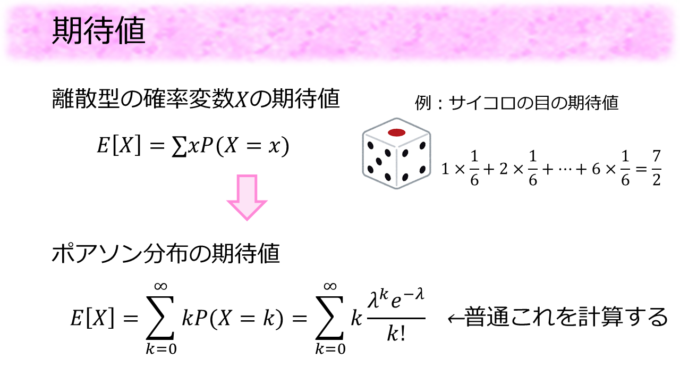
次に期待値について簡単に解説します。確率変数$X$の期待値$E[X]$は$X$がとる値とその値をとる確率を掛け合わしたものを、全て足すことで計算できます。

中学校や高校で1個のサイコロを投げたときに出る目の期待値を以下のように計算したと思います。

$$1\times\frac{1}{6}+2\times\frac{1}{6}+\cdots+6\times\frac{1}{6}=\frac{7}{2}$$

たしかに$X$がとる値とその確率をかけて足し合わせていますね。

ポアソン分布の期待値も定義通りに以下の式から計算できます。

$$E[X]=\sum_{k=0}^{\infty}k\frac{\lambda^ke^{-\lambda}}{k!}$$

実際に以下のような式変形で計算できます。

途中で$k-1=l$と変数変換を行っています。また、指数関数の以下のテイラー展開の結果も用いています。

$$e^x=\sum_{n=0}^\infty\frac{x^n}{n!}$$

計算の結果、ポアソン分布の期待値は$\lambda$であることが確認できました。これは元々の確率変数$X$の定義から予想できていたことであり、予想通りの結果が得られうれしくなります。

参考までにポアソン分布の分散は$X^2$の期待値を計算することによって得ることができます。結果は$\lambda$となり、ポアソン分布では期待値と分散が等しいことがわかります。

さて、このポアソン分布の期待値に関する授業が印象に残っている理由ですが、お客様がお持ちの統計のテキストで、ポアソン分布の期待値の導出にモーメント母関数を用いていたからです。

モーメント母関数は確率変数$X$に対して、

$$M_X(t)=E[e^{tX}]$$
で定義される関数のことです。これは$t$の関数になります。

モーメント母関数$M_X(t)$を$t$で微分することで、

$$M_X^{\prime}(t)=\frac{d}{dt}E[e^{tX}]=E\left[\frac{d}{dt}e^{tX}\right]=E[Xe^{tX}]$$
となりますが、ここで$t=0$とすることで、
$$E[X]=M_X^{\prime}(0)$$
であることがわかります。さらにモーメント母関数を微分していくことで、$E[X^k]$の値も求めることができるのです。

ということで授業の中でお客様とポアソン分布のモーメント母関数を求め、2階まで微分してみました。微分は数Ⅲまでやっている方ならできるかと思います。

その後$t=0$とすることで、以下のようにポアソン分布の期待値と分散を求めることができました。

たしかに定義に沿って求めた結果と同じく、期待値も分散も$\lambda$になりました。めでたしめでたし。

まとめ

今回は最近印象に残った授業としてモーメント母関数を用いたポアソン分布の期待値、分散の求め方を紹介しました。二項分布や正規分布などほかの有名な分布に対してもモーメント母関数を求め、そこから期待値や分散を導出することも可能です。興味を持った方は是非計算してみてください。

モーメント母関数は統計検定準一級や一級で出題されることがあります。このあたりの学習を苦手に感じている方には以下の講座がおすすめです。

統計検定準１級対策

統計検定１級対策

(文/松中)