↓↓↓動画で見たい方はこちら↓↓↓

分数の足し算

分数の足し算を行うには分母を同じにしてから（通分）、分子同士の足し算を行います。また、分母を同じにする（通分）ためには最小公倍数の求め方を知らなければいけません。
　
このように、分数の足し算は整数や小数の足し算と違って一筋縄ではいかないのです。整数や小数の場合は筆算を使ってそれぞれの桁を足すことで和を計算できます。しかし、分数の足し算は単純に分母の数と分子の数を足すことでは求まりません。分数の掛け算は分母と分子をそれぞれ掛ければ答えが分かるので、こんがらがってしまうことがあります。

この記事では分数の足し算に苦手意識がある方向けに足し算の方法をやさしく解説します。
※人気の社会人が算数を学び直す講座↓↓↓
いつか学び直したかった大人の算数講座-半年で6年分を理解する-

なぜ分母と分子同士を足してはいけないのか

上のセクションでは分母と分子同士を足しても分数の和が求まらないことを説明しました。
実際にこのように計算することの問題点を確認します。

例として、$\frac{1}{2}$+$\frac{1}{2}$を考えてみましょう。$\frac{1}{2}$の分子と分母をそれぞれ足すと$\frac{2}{4}$が求まりますが、これでは間違いです。$\frac{1}{2}$は2個あるうちの1個なので、全体の半分と考えることができます。また、$\frac{2}{4}$も4個あるうちの2個なので、同様に全体の半分と考えられます。

ここでは、半分と半分を足しているので、合計は1になるはずですが、計算した答えは$\frac{1}{2}$と同じ量になってしまいます。

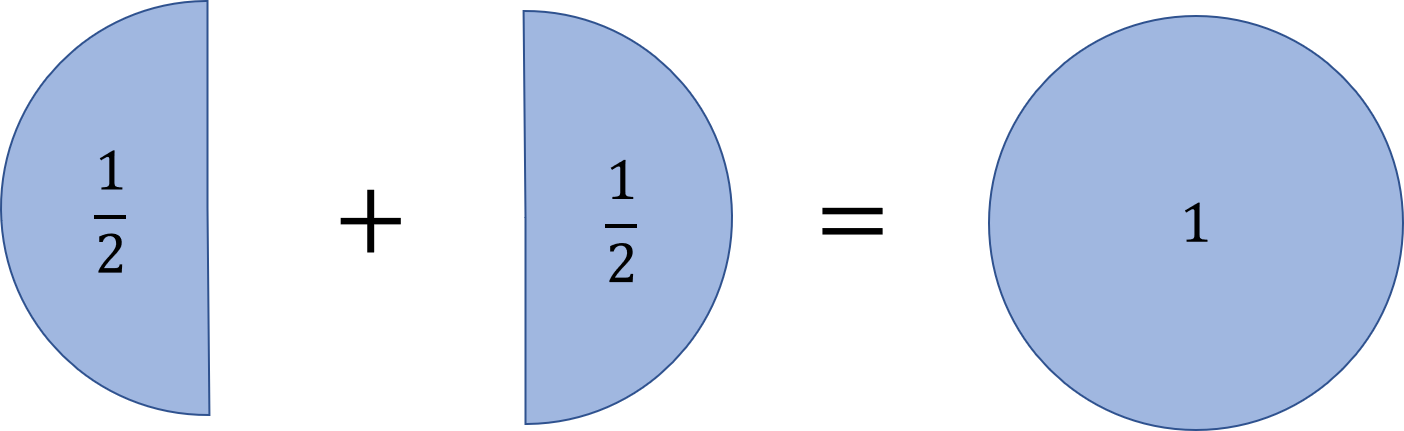
分数を上にあるように円で考えてみます。分母にある数が円をいくつの等しいピースに分けるかを決めるとします。$\frac{2}{4}$であれば、分母は4なので全体を4等分したピースができます。また、分子の数はそのピースがいくつあるかを示します。$\frac{2}{4}$は分子が2なので4分割されたピースが2個です。よって、$\frac{2}{4}$が円の半分になることが分かります。

分数の分母を足してしまうと、円を等分する個数が増えてしまいます。上の例では、2等分が4等分になります。本当は半円を2つ足すということなのに各ピースが4等分された円のサイズに変わってしまっているので正しい答えが求まらないことが分かります。

通分

分数の足し算を行うためにはまず通分をすることが必要です。

「通分とは」の記事では通分やその活用について詳しく説明されているので興味のある方はそちらを参照すると良いでしょう。

足し算をする分数を通分するということは$2$つの分数の分母を同じ数字に揃えるということです。分母と分子に同じ数を掛けることで分数の値を変えないまま、分母の数字を共通のものに変えることができます。
　
分母の数を共通のものに揃えるために分子分母に数を掛けるので、それぞれの分母の数の倍数の中で共通する数を見つけれる必要があります。この共通する倍数のことを公倍数とよび、2つの数の公倍数の中でも最小のものを最小公倍数とよびます。最小公倍数を用いるとそれぞれの分母に掛ける数が小さく済むので、簡単に通分することができます。

最小公倍数を見つける

通分を行うためには最小公倍数を見つけなければなりません。このセクションで紹介する方法は、簡単で初心者向けの方法になります。

分母の倍数を書き出していくことによって公倍数を見つけることができます。

例えば、$\frac{1}{6}$と$\frac{1}{22}$であれば、

$6$の倍数: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66
$22$の倍数: 22, 44, 66

となり、$66$が$6$と$22$の公倍数であることが分かります。

計算に慣れた方は、より大きい分母から倍数をいくつか書き出してみると良いでしょう。小さい方の分母で倍数が割り切れたらそれが最小公倍数と分かります。公倍数は$2$つの数の倍数であることから、$2$つの数で割り切れます。このことを利用すると、より早く最小公倍数が見つかるでしょう。

分数を足してみる

では実際に分数の足し算をしてみましょう。$\frac{4}{7}+\frac{3}{4}$を考えます。

はじめに、分母の最小公倍数を求めて通分をします。$7$の倍数は$7, 14, 21, 28, 35, 42$であり、$4$の倍数は$4, 12, 16, 20, 24, 28, 32$であるため、最小公倍数は28と分かります。いま、$7$を$28$にしたので、$\frac{4}{7}$の分子分母を$4$（$=28÷7$）で掛けることで分数の値を変えずに分母を変えることができます。同じように、$\frac{3}{4}$は分母分子に$7$（$=28÷4$）を掛けます。
　
このようにして、$\frac{4}{7}+\frac{3}{4}$=$\frac{16}{28}+\frac{21}{28}$と書き換えることができます。最後に、分子の値を足して、$\frac{37}{28}$が求められます。

分数の足し算の活用

日常では分数を使う機会は意外と多いです。例えば、計量カップには$\frac{1}{2}$の目盛りがついていることがあります。また、オンデマンドの講座を受講されたことがある方なら、進捗率が4/12などという風に表されているのを見たことがあるかもしれません。そして、分数の足し算を用いる機会も日常に隠れています。例えば仕事でアンケートを取り、「賛成」が$\frac{1}{3}$、「おおむね賛成」が$\frac{1}{2}$であった場合、二つを足すことで結果を別の見方でデータを解釈することができます。

参考: 通分とは【算数からやさしく解説】

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/須藤>