一筆書きの数学からモノクロデザインへ
公開日
2020年7月1日
更新日
2025年9月17日

こんにちは。和からの数学講師の岡本です。
突然ですが、田んぼの「田」の字、一筆で書けますか?つまり、同じ道を通らずに「田」の字を形作ることはできますか?例えば、「日」という字は
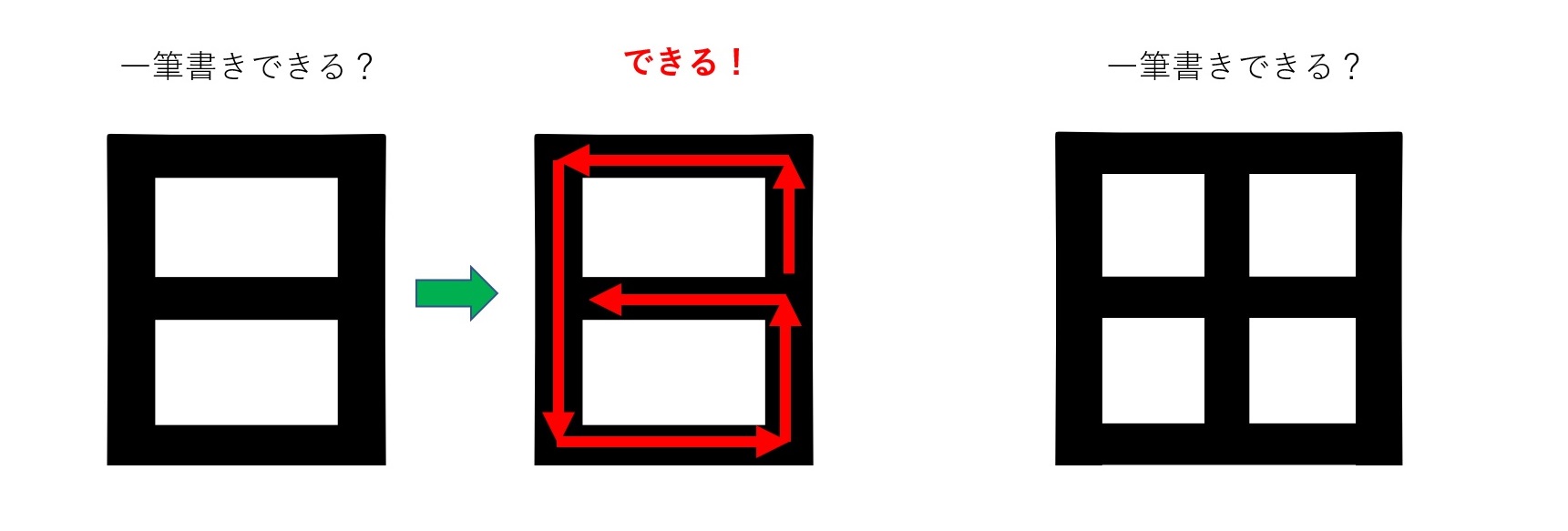
のように一筆で描けます。果たして田んぼの「田」は一筆で書けるでしょうか?
この記事の主な内容
1.一筆書き問題
あれこれ試してみても、「田」の字の一筆書きできそうもありません。実をいうと、「田」の字は一筆書き不可能です。これは頑張って全て方法を試してみればわかります。 では、「中」という字はどうでしょう?実は「中」の字は次の図のように一筆書き可能なのです。 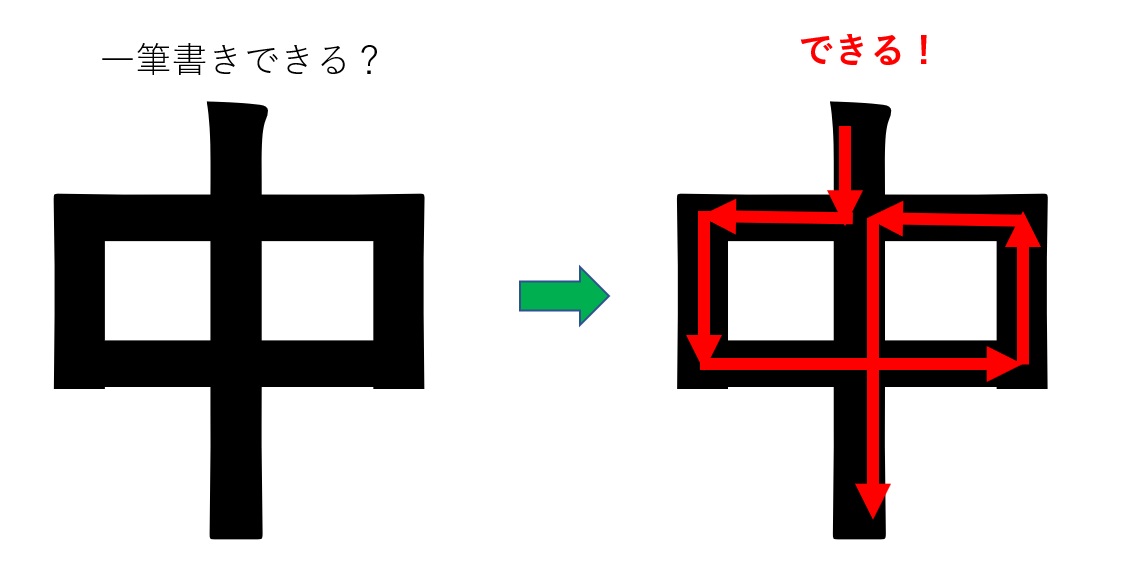 一筆で書ける「道順」が1つでも見つかりさえすればいいのですが、結果的に不可能である場合、全ての道順を知らべ尽くさなくてはならず、途方もない作業となってしまいます。。。 実はこのような問題は「グラフの一筆書き問題」として数学的にとらえることができます。
一筆で書ける「道順」が1つでも見つかりさえすればいいのですが、結果的に不可能である場合、全ての道順を知らべ尽くさなくてはならず、途方もない作業となってしまいます。。。 実はこのような問題は「グラフの一筆書き問題」として数学的にとらえることができます。
2.グラフ理論(ケーニヒスベルクの橋)
数学では、先のような問題を「グラフ理論」の問題として考えます。グラフ理論とは、点の集合とそのつながりのみに注目する、比較的新しい数学の分野です。データを可視化する際に使われる“グラフ”とはちがい、“ネットワーク”を定式化したものと考えられます。グラフ理論の始まりは18世紀の「ケーニヒスベルクの橋の問題」であるといわれています。
「ケーニヒスベルクの橋の問題」とは、ヨーロッパのケーニヒスベルクという街(当時の東プロイセンの首都)にある7つの橋に関する、以下のような問題です。
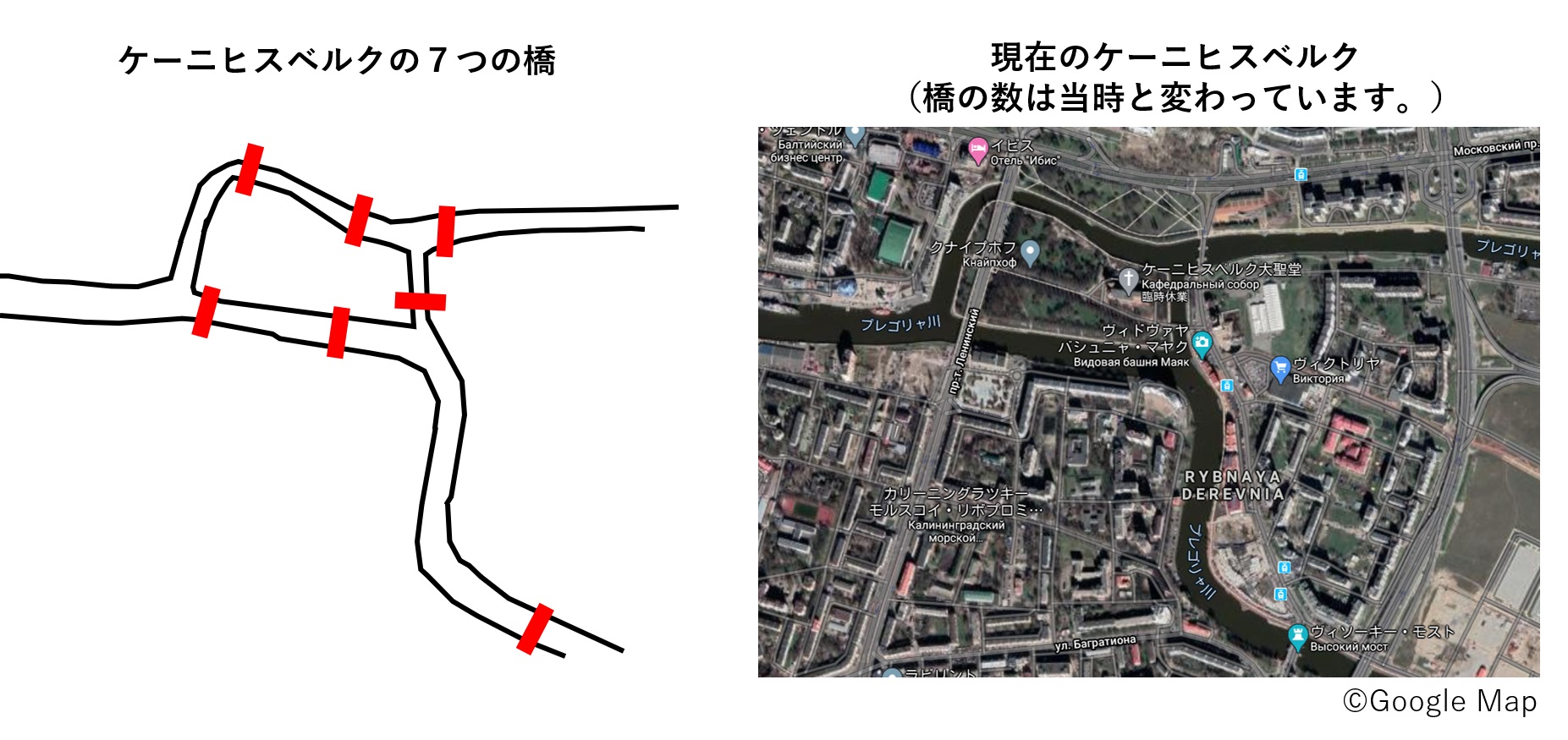
この問題は“難問”として、長い間無解決でしたが、この問題を解決した人物が現れます。数学界の“ゴッド”ことレオンハルト・オイラーです。オイラーに関しては以前のマスログで詳しく解説していますのでよろしければこちらの記事も併せてご覧ください。
彼はこの問題を単純化することを考えました。つまり、街の配置や道の曲がり具合などを全て無視し、4つの地点に「たどり着けるかどうか」をつながりだけで議論しようとしたのです。そう、これこそ、点とそのつながりの学問「グラフ理論」のはじまりでした。彼はこのケーニヒスベルクの街と橋の構造を極端に単純化し、グラフの一筆書き問題に帰着させました。
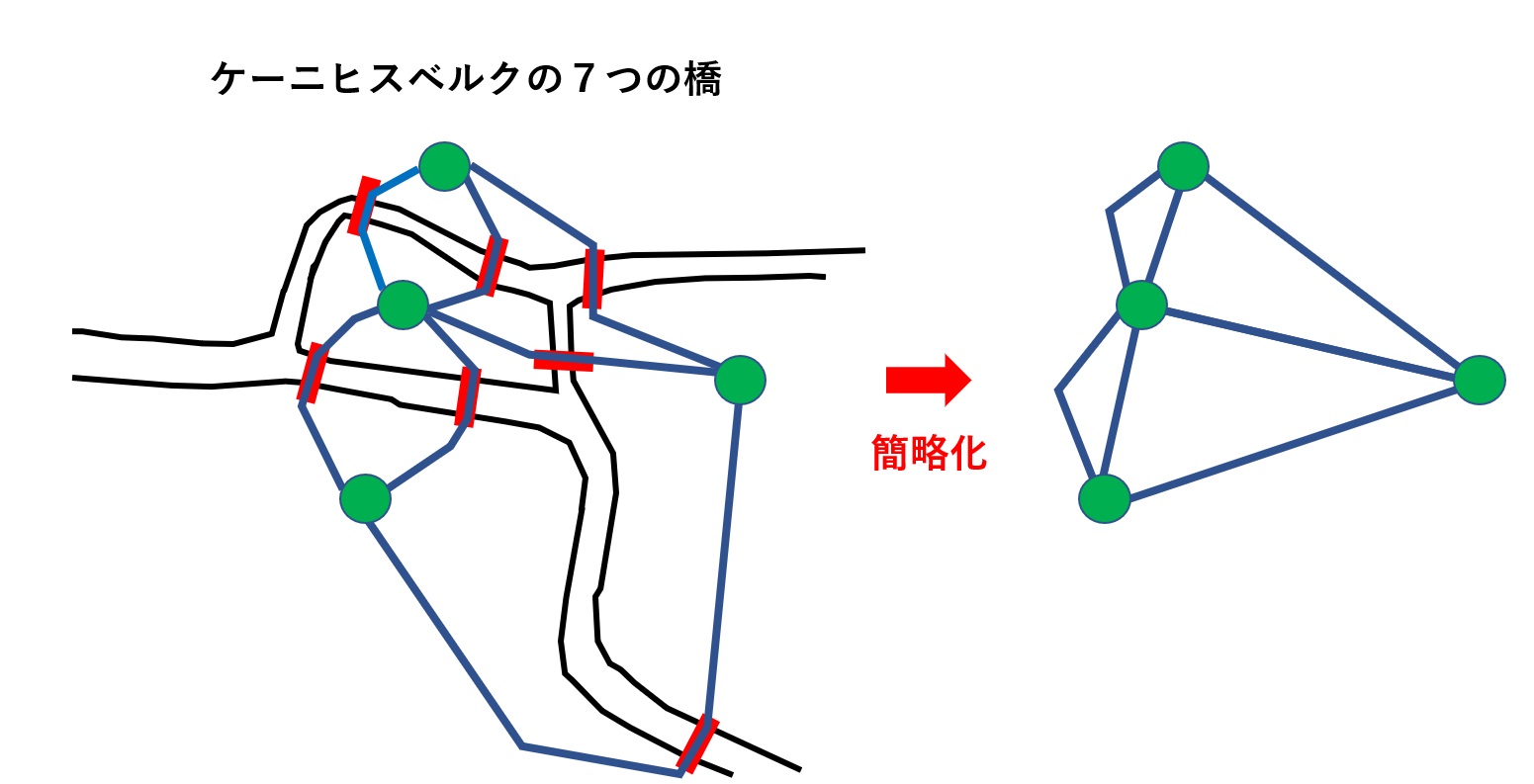
さまざまな情報を無視するという、エキセントリックな考え方は当時としては非常に斬新で、数学の世界を大きく動かしました。このグラフ理論の考え方から「トポロジー」と言われる“柔らかい幾何学”も誕生しました。トポロジーに関しては以前「RPGのワールドマップ」という題材でマスログで紹介しました。興味のある方は是非ご覧ください。
3.一筆書き可能性に関する定理
さて、ケーニヒスベルクの橋を単純化することで「グラフ」を得ることができました。
このグラフの点のことを「頂点(vertex)」、つながっている線(曲がっていても、折れていてもいい)のことを「辺(edge)」といいます。
なお、今日扱う「グラフ」とは頂点が全てつながっており、頂点の数も高々有限個である、「連結有限グラフ」を考えることにします。
まずは頂点について観察してみます。グラフの頂点からは辺が生えているように見えます。何本辺が生えているかは頂点によって様々です。ここで、偶数本生えている頂点を「偶頂点」、奇数本生えている頂点を「奇頂点」と呼ぶことにします。
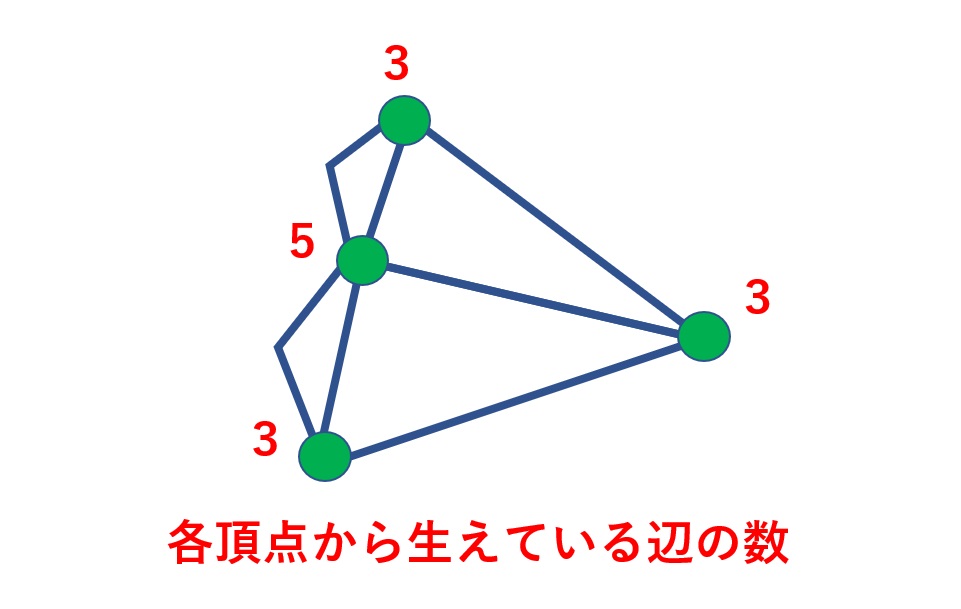
ケーニヒスベルクの橋のグラフに関して偶頂点と奇頂点を観察すると、全て奇頂点であることがわかります。
実は頂点の情報だけでそのグラフが一筆書きできるかどうか判別することができるのです!!
定理(オイラー)
なんということでしょう。。。数学ってすごいですよね。。。しかもこの「奇頂点が0個または2個」という条件は「必要十分条件」にもなっています。。。!
つまり、奇頂点の数が0個でも2個でもなかった瞬間にそのグラフは一筆書き不可能であることが示されるのです。。。!!
この定理を使うと、ケーニヒスベルクの橋の問題は瞬殺です。そう、奇頂点が4つなので、一筆書き不可能なのです。つまり問題にあるように全ての橋を1度だけ通って元の場所に戻ることは不可能だったのです。オイラーはこのような考察からケーニヒスベルクの問題を否定的に解決しました。恐ろしくあっさりと解決されてしまいました。
この定理を使うと、田んぼの「田」も一瞬で解決できます。次の図のように「田」の字をグラフと考え、偶頂点と奇頂点の数を数えてみます。
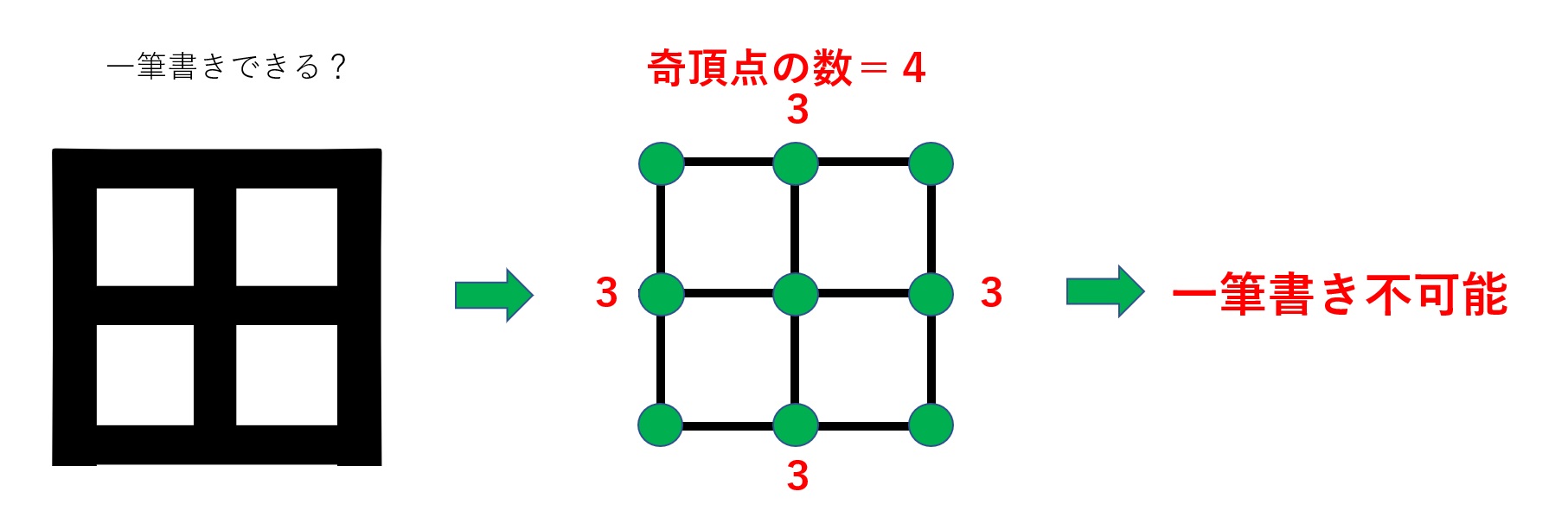
すると、奇頂点が4つ。この時点で一筆書き不可能であることがわかります。今後もし、「これ一筆書きできますか?」という問題が出題されたとき、奇頂点を数えるだけで瞬時に解決できます。我々はいま、とんでもないウェポンを手に入れたのです!
4.モノクロデザインへ
もう少し観察してみましょう。一筆で線を書くとき、以前自分が通った線と交わることがあります(下図参照)。このときこの交点が「頂点」となり、その頂点からは4本の辺が生えていると見れます。つまり、線が交わっているところは「クロスする」と偶頂点に、その交点で止まれば奇頂点になります。
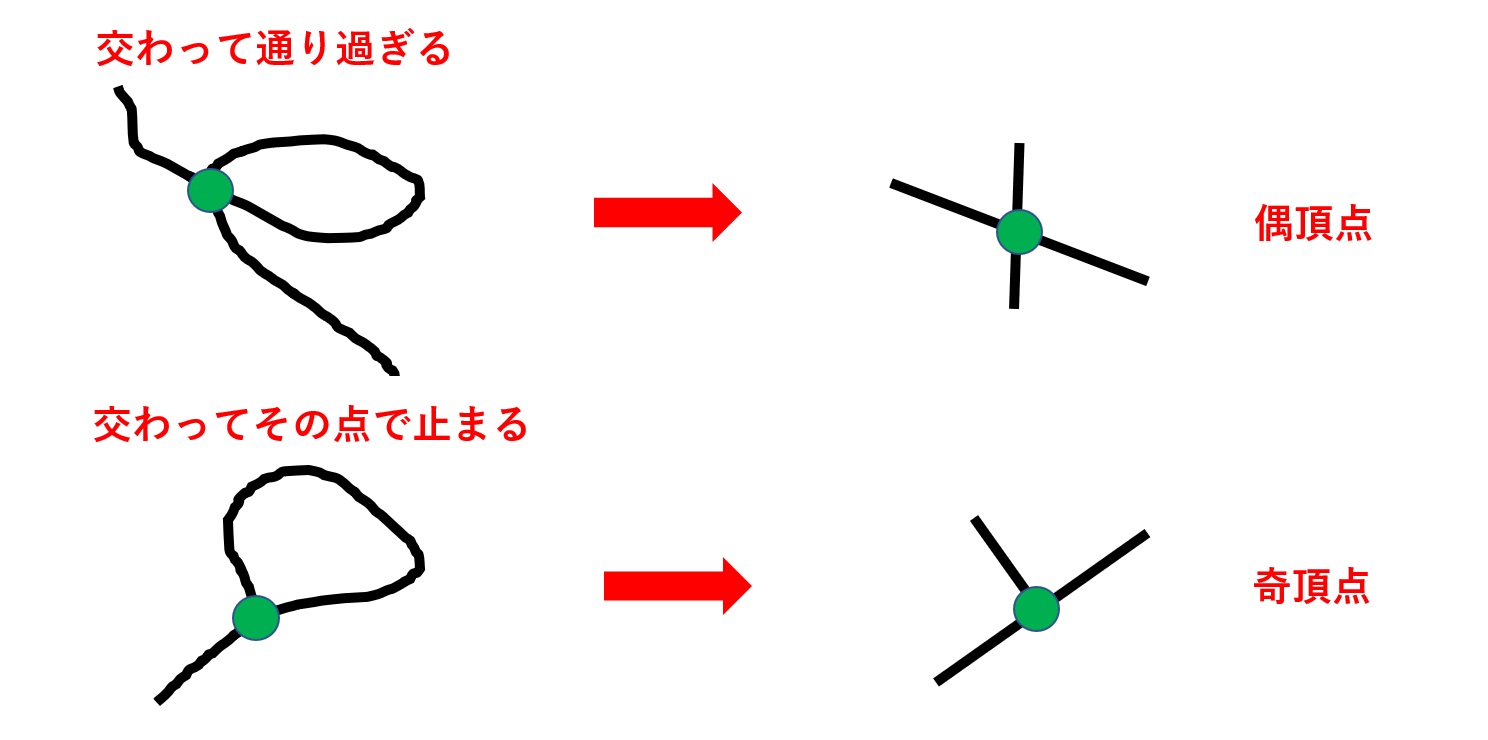
このことから「奇頂点が2」ということはそれぞれの点が「始点(スタート地点)」と「終点(ゴール地点)」であり、「奇頂点が0個」ということは、始点と終点が同じ、“一筆書きのループ”であることがわかります。この「一筆書きループ」について、驚くべき性質を最後にご紹介します。
定理
ループの模様によっていくつかのエリアに分けられます。なんと、そのエリアは2色(例えば白と黒)で塗り分けられるというのです!!例えば次のようになります。
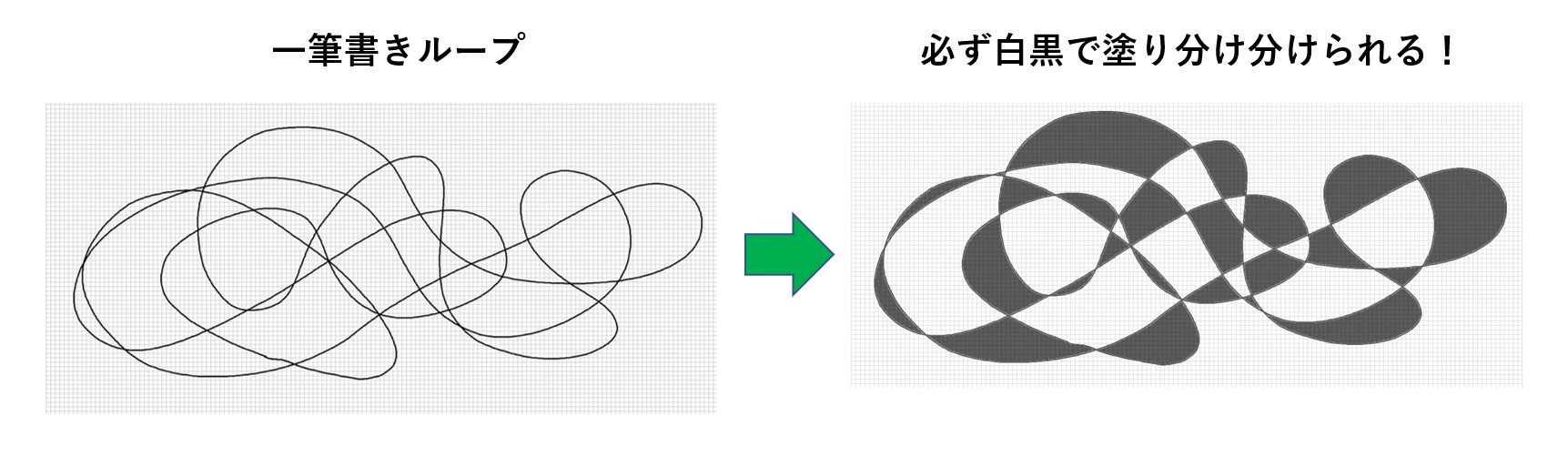
美しいですね!!このような白黒塗分けることは、切り絵の世界では「切り抜く部分」と「残す部分」と分けるため、下絵の際白黒のデザインにすることが一般的です。実際に岡本はこの性質を利用して切り絵のデザインを制作することもあります。岡本の切り絵に関しては以下のマスログに掲載しています。興味のある方は是非ご覧ください。
5.さいごに
いかがでしたでしょうか。田んぼの「田」の字から広がったグラフ理論の世界。しかもその美しい性質がモノクロのデザインや切り絵などのアートの世界にも応用できるというのは非常に興味深い数学の一面だと思います。今回も塗り絵が出てきましたので、「世界一美しい数学塗り絵」をご紹介します。
また、グラフ理論に関しては「グラフ理論序説(プレアデス出版)」がおすすめです。グラフ理論の基本的な内容から様々な応用まで非常にまとまってあります。なお著者の仁平政一先生は和の講師として活躍されています。
数学的なデザインやアートに関する無料セミナーも開催しておりますので、興味のある方は是非ご参加ください。
また、岡本の数学アート作品、デザイングッズはこちらから
和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。
<文/岡本健太郎>

















