感銘を受けた数学「オイラーの五角数定理」

ロマンティック

公開日

2020年4月29日

更新日

2020年4月29日

　今日は誠に勝手ながら和の講師岡本が狂おしいほど好きな数学の定理の１つ「オイラーの五角数定理」について熱く語っていこうと思います。
新型コロナの影響もあり、ご自宅で１日を過ごすことが多くなってきたと思います。数学の話題で一息したい、あるいはしっかりと式を追って数学をやりたい！という方に朗報です。割としっかりした内容で数式が盛りだくさんな記事になりました。計算を追いたい方は紙とペンを用意して、ぜひ最後まで雰囲気を感じていただければと思います。

この記事の主な内容

１．ところで「五角数」ってなに？

みなさんは五角数ってご存じでしょうか？あんまりメジャーではないと思います。五角数とは下の図のように、点を五角形に沿って規則的に並べたときの点の個数のことです。

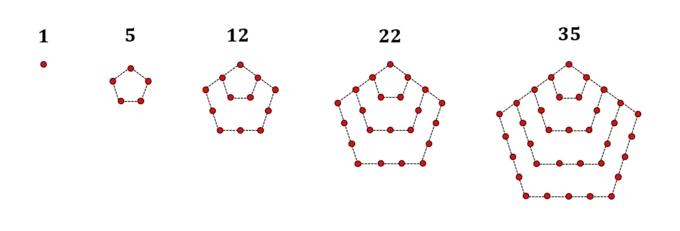
最初は$1$、続いて$5$, $12$, $22$, $35$,…　と続いていきます。では$n$番目の五角数はどう表されるでしょうか？実は次のような漸化式

\begin{align*}a_{n+1}=a_n+3n+1\end{align*}

で特徴付けられています。この漸化式を解くと初期値が$a_1=1$ であることから一般項は次のように表されます。

\begin{align*}a_n=\frac{1}{2}n(3n-1)\end{align*}

今日の主役はこの五角数です。

２．オイラーの五角数定理

かの有名な大数学者レオンハルト・オイラーの名を冠した「オイラーの五角数定理」。早速ですがその主張を述べておきましょう。

定理（オイラーの五角数定理 1750年）

以下の等式（恒等式）が成り立つ。

$$\prod_{m\in \mathbb{N}}(1-q^m)=\sum_{n\in \mathbb{Z}}(-1)^n q^{\frac{1}{2}n(3n-1)} $$

ここで、$q$ は $|q|<1$を満たす複素パラメータとする（あまり気にしなくていいです）。

いかがでしょうか。私はこの美しすぎる等式を見て目がくらんでしまいました。もはやアートです！！！右辺の $q$ の肩にはなんと「五角数さん」がいらっしゃるのです…！神々しいです…。
左辺は「全て自然数 $m$ に対して積」を考えており、右辺では「全ての整数 $n$ に対して和」を考えています。こうしたいわゆる「無限積＝無限和」という等式はリーマンゼータ函数の等式

$$\prod_{p:\text{素数}}\frac{1}{1-p^{-s}}=\sum_{n\in \mathbb{N}}\frac{1}{n^s}$$

と同様になんとも言えない妖艶な雰囲気を醸し出しており、私の大好物です（なお、この等式の左辺も「オイラー積」と、やはりオイラーの名が冠されています）。
さて、この五角数定理ですが、少し書き下してみましょう

\begin{align*}(1-q)(1-q^2 )(1-q^3 )(1-q^4)\cdots=1-q-q^2+q^5+q^7-q^{12}-q^{15}+q^{22}+q^{26}-\cdots\end{align*}

さらにこの等式のやばさを体感していただくために、左辺を有限個の積で計算してみましょう。

\begin{align*}(1-q)(1-q^2 )&=1-q-q^2+q^3\\
(1-q)(1-q^2 )(1-q^3 )&=1-q-q^2+q^4+q^5-q^6\\
(1-q)(1-q^2 )(1-q^3 )(1-q^4 )&=1-q-q^2+2q^5-q^8-q^9+q^{10}\\
(1-q)(1-q^2 )(1-q^3 )(1-q^4 )(1-q^5 )&=1-q-q^2+q^5+q^6+q^7-q^8-q^9-q^{10}+q^{13}+q^{14}-q^{15}\end{align*}

最終的には無限に掛け合わせるので、右辺は形があまりはっきりしないですが、どうやら絶妙に各項がキャンセルし合い、生き残る項はなんと五角数の冪のみというのが五角数定理です！なんとも不思議ですね。

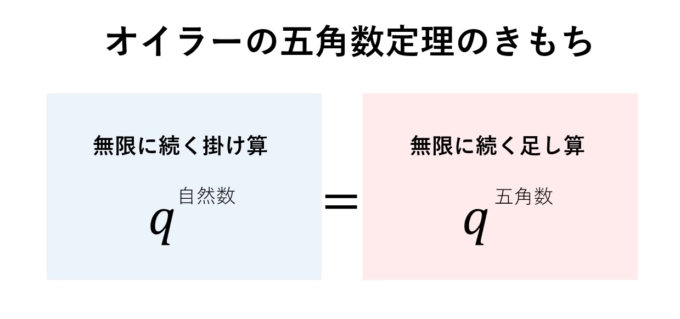
右辺は$1,2,3,4,\ldots$と続く、いわばもっとも自然な数の並びの「掛け算」です。それが五角形を起源とする数の「足し算」として結び付けられる…。どうやら「五角形」というのは実は非常に自然な形なのかもしれません。
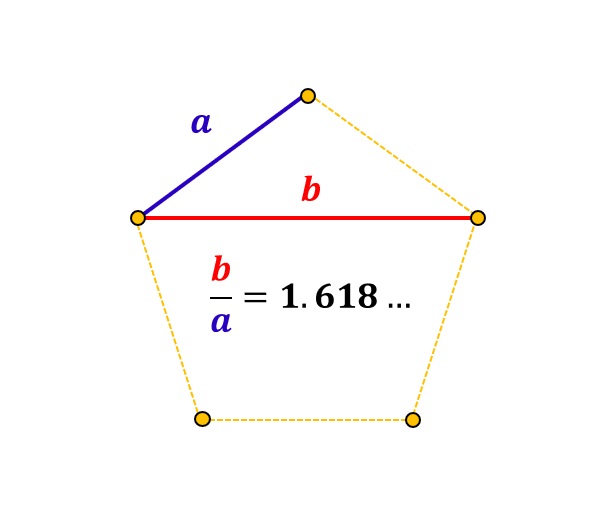
なお、話は変わりますが正五角形は各頂点を線で結ぶことによって２種類の長さの線が得られます。この２つの線分の比は「黄金比($=1.618\cdots$)」になっています。

芸術の世界でも「美しい比率」「神の比率」と言われている黄金比ですが、実は正五角形との深い関係もあったのですね！

３．五角数定理の証明

さて、五角数定理の証明ですが、組み合わせ論的手法や解析的手法などさまざまな方法が知られています。ここではヤコビの三重積公式を使った証明と $q$-超幾何級数を用いた証明を簡単ではありますがご紹介いたします。ぜひ追ってみてください。

3-1記号の準備

ここからは無限に積を考えることが多々あります。そこで次のような記号を使います。

\begin{align*}\prod_{m=1}^N(1-q^{m-1}x)&=(1-x)(1-qx)(1-q^2x)\cdots(1-q^{N-1}x)=(x;q)_N\\
\prod_{m=1}^{\infty}(1-q^{m-1}x)&=(1-x)(1-qx)(1-q^2x)\cdots=(x;q)_{\infty}\end{align*}

$(x;q)_N$や、その無限積版 $(x;q)_{\infty}$ を $q$-ポッホハマー記号といいます。

3-2ヤコビの三重積公式からの証明

かなり詳細は省略しますが、まずはヤコビの三重積公式というものを証明します。流れはまず、有限積版の$(x;q)_N (q/x;q)_N$ を計算し、極限操作 $N\to \infty$で$(x;q)_{\infty} (q/x;q)_{\infty}$を求めます。ちょっとした式変形と「$q$-二項定理」

$$\prod_{m=1}^N(1+q^{m-1}x)=(-x;q)_N=\sum_{n=0}^N\frac{(q^{N-n+1};q)_n}{(q;q)_n}q^{\frac{1}{2}n(n-1)}x^n$$

を用いることで

\begin{align*}(x;q)_N(q/x;q)_N&=(-1)^N q^{\frac{1}{2}N(N-1)}x^{-N}(q^{-N}x;q)_{2N}\\[0.5em]
&=\sum_{n=0}^{2N}\frac{(q^{2N-n+1};q)_n}{(q;q)_n}q^{\frac{1}{2}(-N+n)(-N+n-1)}(-x)^{-N+n}\end{align*}

を得ます。またここで、$(x;q)_n=\frac{(x;q)_{\infty}}{(q^n x;q)_{\infty}} $という変形を考え整理すると

$$(x;q)_N(q/x;q)_N=\sum_{n=-N}^N\frac{(q^{N-n+1};q)_{\infty}(q^{N+n+1};q)_{\infty}}{(q^{2N+1};q)_{\infty}(q;q)_{\infty}}q^{\frac{1}{2}n(n-1)}(-x)^n$$

が得られます。ここで極限 $N\to \infty$ を考えると

$$(x;q)_{\infty}(q/x;q)_{\infty}=\lim_{N\to \infty}(x;q)_N(q/x;q)_N=\frac{1}{(q;q)_{\infty}}\sum_{n=-\infty}^{\infty}q^{\frac{1}{2}n(n-1)}(-x)^n.$$

両辺に$(q;q)_{\infty}$を掛けることでヤコビの三重積公式を得ました。

$$(x;q)_{\infty}(q/x;q)_{\infty} (q;q)_{\infty}=\sum_{n=-\infty}^{\infty}q^{\frac{1}{2}n(n-1)}(-x)^n.$$

仕上げです。上の公式において $x\to q$, $q\to q^3 $という、うまい置き換えを行います。すると左辺は

$$(q;q^3)_{\infty}(q^2;q^3)_{\infty}(q^3;q^3)_{\infty}=\prod_{m=1}^{\infty}(1-q^{3m-2})(1-q^{3m-1})(1-q^{3m})=\prod_{m=1}^{\infty}(1-q^m )$$

となり、右辺は

$$\sum_{n=-\infty}^{\infty}q^{\frac{3}{2}n(n-1)}(-q)^n=\sum_{n=-\infty}^{\infty}(-1)^nq^{\frac{3}{2}n(n-1)+n}=\sum_{n=-\infty}^{\infty}(-1)^n q^{\frac{1}{2}n(3n-1)}$$

となります。つまり等式

$$\prod_{m=1}^{\infty}(1-q^m) =\sum_{n=-\infty}^{\infty}(-1)^n q^{\frac{1}{2}n(3n-1)}$$

が証明されました！うまい変形ですね…！うますぎて馬になっちゃいそうです。なにはともあれ、これでオイラーの五角数定理はもうあなたのものです！！

3-2 $q$-超幾何級数を用いた証明

突然ですが $q$-超幾何級数という、ややマニアックな函数を導入します。

$$F_q (a,b;x)≔1+\sum_{n=1}^{\infty}\frac{(aq;q)_n}{(bq;q)_n} x^n $$

$q$ は先ほどと同様に $|q|<1$ を満たす複素パラメータとしておきます。ちょっとした変形により$F_q (a,b;qx)$ と$F_q (aq,b;x)$ の関係式

\begin{align*}F_q (a,b;x)&=\frac{1-b}{1-x}+\frac{b-aqx}{1-x} F_q (a,b;qx)\\
F_q (a,b;x)&=-\frac{(1-b)aq}{b-aq}+\frac{(1-aq)(b-aqx)}{b-aq} F_q (aq,b;x)\end{align*}

が得られます。これを合わせて$F_q (aq,b,qx)$との関係式が計算できます。

$$F_q (a,b;x)=\left(\frac{1-b}{1-x}\right)\left(1-\frac{b-aqx}{b-aq}aq\right)+\frac{(1-aq)(b-aqx)(b-aq^2 x)}{(1-x)(b-aq)} F_q (aq,b;qx).$$

この関係式において両辺に$1-x$ を書けると

$$(1-x)F_q(a,b;x)=(1-b)\left(1-\frac{b-aqx}{b-aq}aq\right)+\frac{(1-aq)(b-aqx)(b-aq^2 x)}{b-aq}F_q(aq,b;qx).$$

さらに$a=x,b=0$とし、$f_q (x)=(1-x)F_q (x,0;x)$とおくと$f_q(x)$に関する関係式

$$f_q (x)=1-qx^2-q^2 x^3f_q(xq)$$

が得られます。これにより展開式

$$f_q(x)=\sum_{n=1}^{\infty}(-1)^n q^{\frac{1}{2}n(3n-1)}x^{3n-1}+\sum_{n=0}^{\infty}(-1)^n q^{\frac{1}{2}n(3n+1)}x^{3n}$$

が得られます。これもまた見事な式変形です。一方、反復法と言われる手法により

$$\lim_{x \to 1}⁡(1-x)F_q(a,b;x)=\frac{(aq;q)_{\infty}}{(bq;q)_{\infty}}$$

が得られます。これと$f_q(x)$の展開式を合わせることで

$$(q;q)_{\infty}=\sum_{n=0}^{\infty}(-1)^n q^{\frac{1}{2}n(3n+1)}+\sum_{n=1}^{\infty}(-1)^n q^{\frac{1}{2}n(3n-1)}=\sum_{n=-\infty}^{\infty}(-1)^n q^{\frac{1}{2}n(3n-1)}$$

つまり、オイラーの五角数定理が証明されました…。鮮やかです。もう何でしょうね、全ての式が美しく見えてきます。ずっと登場している複素パラメータの $q$ なんて、もうそのフォルム自体が美しくないですか？

この世には、アルファベット $q$ が大好きな人類（いわゆる「 $q$ -人類」）と、そうでない人類の２つに分かれます。 岡本は前者です。

※【パラメータ $q$ について】実は $q$-解析という数学の一分野があります。量子群や組み合わせ論、結び目不変量、特殊関数、ラマヌジャンのテータ函数など様々な話題と結びついており、いまでも多くの人を魅了しています（と信じています）。

４．終わりに

いかがでしたでしょうか？もちろん細かい議論や式変形などは言及していませんが、五角数定理の証明の雰囲気と美しさを少しでも感じて頂ければ幸いです。なお、今回の内容は「オイラーに学ぶ『無限解析序説』への誘い（野海正俊）」と「Basic Hypergeometric Series and Applications (Nathan J. Fine)」を参考にしています。