動画で見たい方はこちら↓↓↓

※人気の社会人が算数を学び直す講座↓↓↓
いつか学び直したかった大人の算数講座-半年で6年分を理解する-

こんにちは。和からの数学講師の岡本です。以前、「感銘を受けた数学」シリーズとして、岡本が狂おしいほど好きなオイラーの五角数定理をマスログでご紹介しました。

感銘を受けた数学「オイラーの五角数定理」

今回も岡本が個人的に心にグッと来た数学をご紹介していこうと思います。みなさんは「三平方の定理」をご存知でしょうか？「ピタゴラスの定理」とも言われています。そうです、直角三角形のアレです。

直角三角形の一番長い辺（斜辺といいます）の長さを、残りの辺の長さから割り出せる公式です。中学・高校と、何度もお世話になり、数学ではもはや「おなじみ」となっている三平方の定理。

しかし、みなさんは「証明」できますか？今日はこの三平方の定理の多様な証明方法をひたすらご紹介いたします。その実に見事で、美しい証明方法をご堪能ください。

１．三平方の定理の証明その１

まずは良く知られた、最もポピュラー（？）な証明方法をご紹介します。

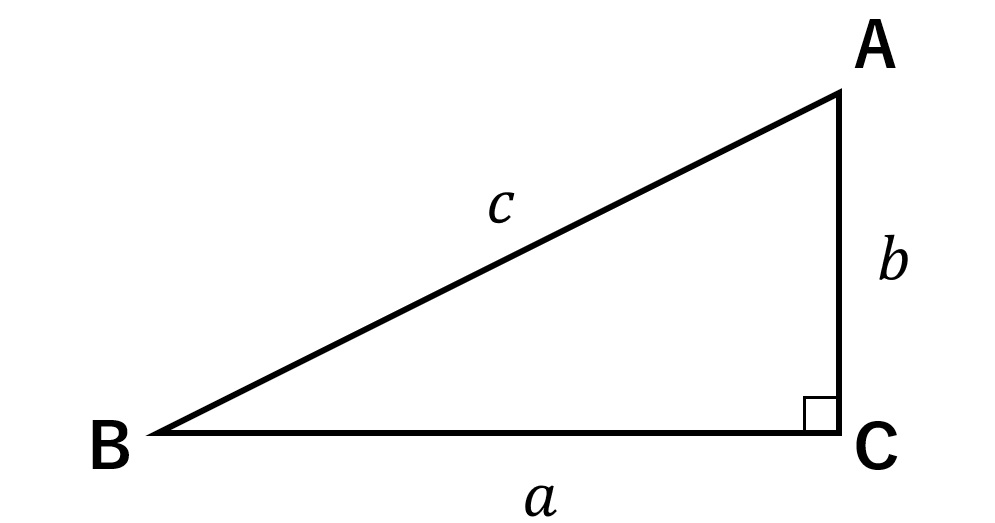
まず、直角三角形ABCを準備します。長さが\(a\)と\(b\)（\(a>b\)とします）、斜辺を\(c\)としましょう。以降、この直角三角形をベースにお話していきます。

まずはこの三角形を４つ用意し、下の図のように並べます。すると、大きな正方形と内側にも正方形が出来上がります。このとき大きな内側の正方形の面積を２通りで表します。

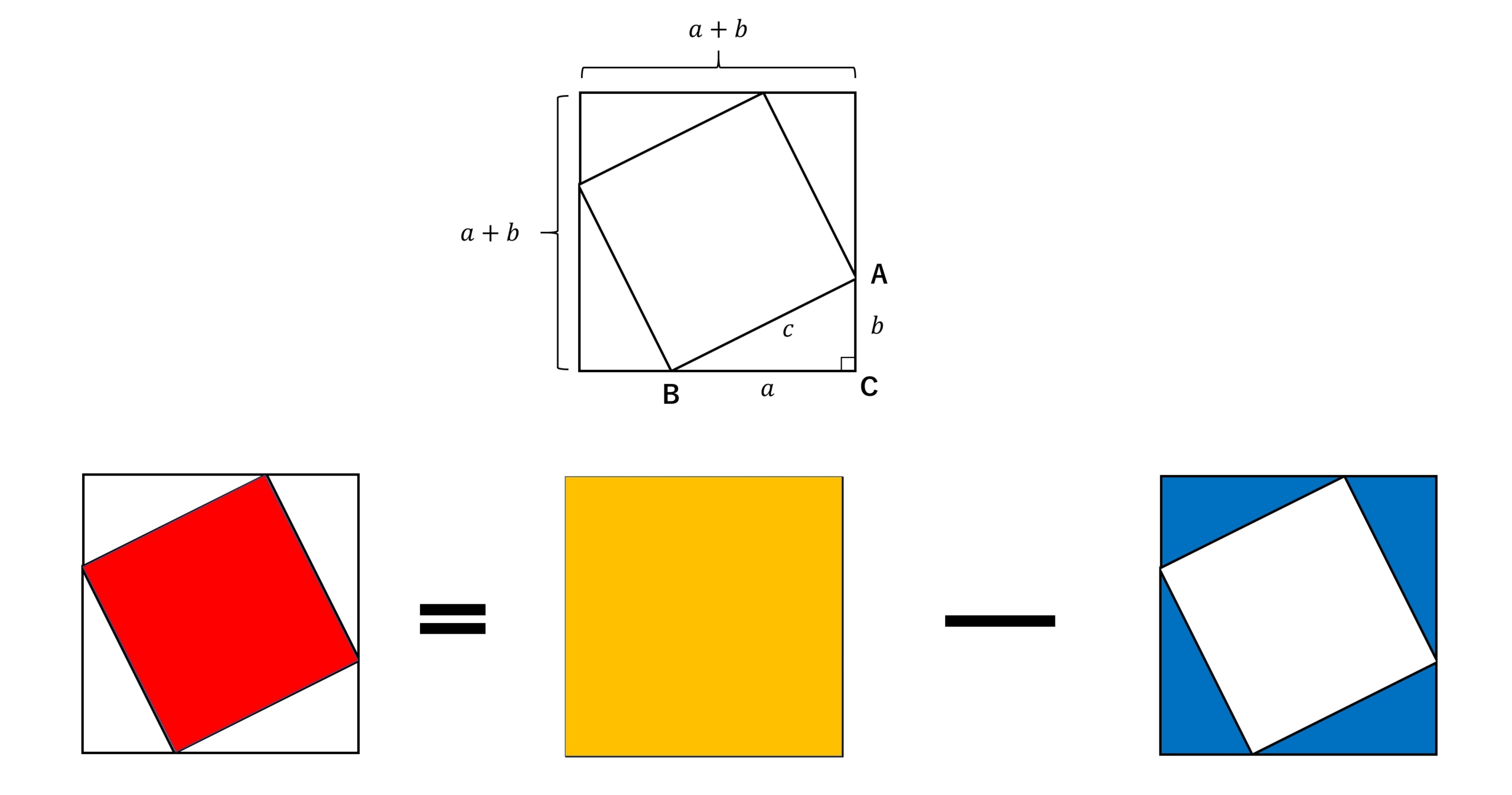
まず赤の部分は一辺の長さが\(c\)の正方形なので、その面積は\(c^2\)。また、別の計算方法として、外側の大きな正方形（一辺の長さは\(a+b\)）から直角三角形４つ分の面積を引くことで求められます。ここで三角形の面積は底辺×高さ÷２ということで、\(ab/2\)となります。これを４つ分引くわけです。

このとき計算は

\begin{align*}(a+b)^2-4\cdot \frac{ab}{2}=a^2+2ab+b^2-2ab=a^2+b^2\end{align*}

となり、これが内側の面積\(c^2\)と一致する、つまり

\begin{align*}a^2+b^2=c^2\end{align*}

が証明されました。シンプルかつ美しいですね！では次の証明に進みましょう！

２．三平方の定理の証明その２

次の証明は「方べきの定理」を使います。方べきの定理にはいくつかバリエーションがありますが、今回使う形のものだけ簡単にご紹介いたします。

 

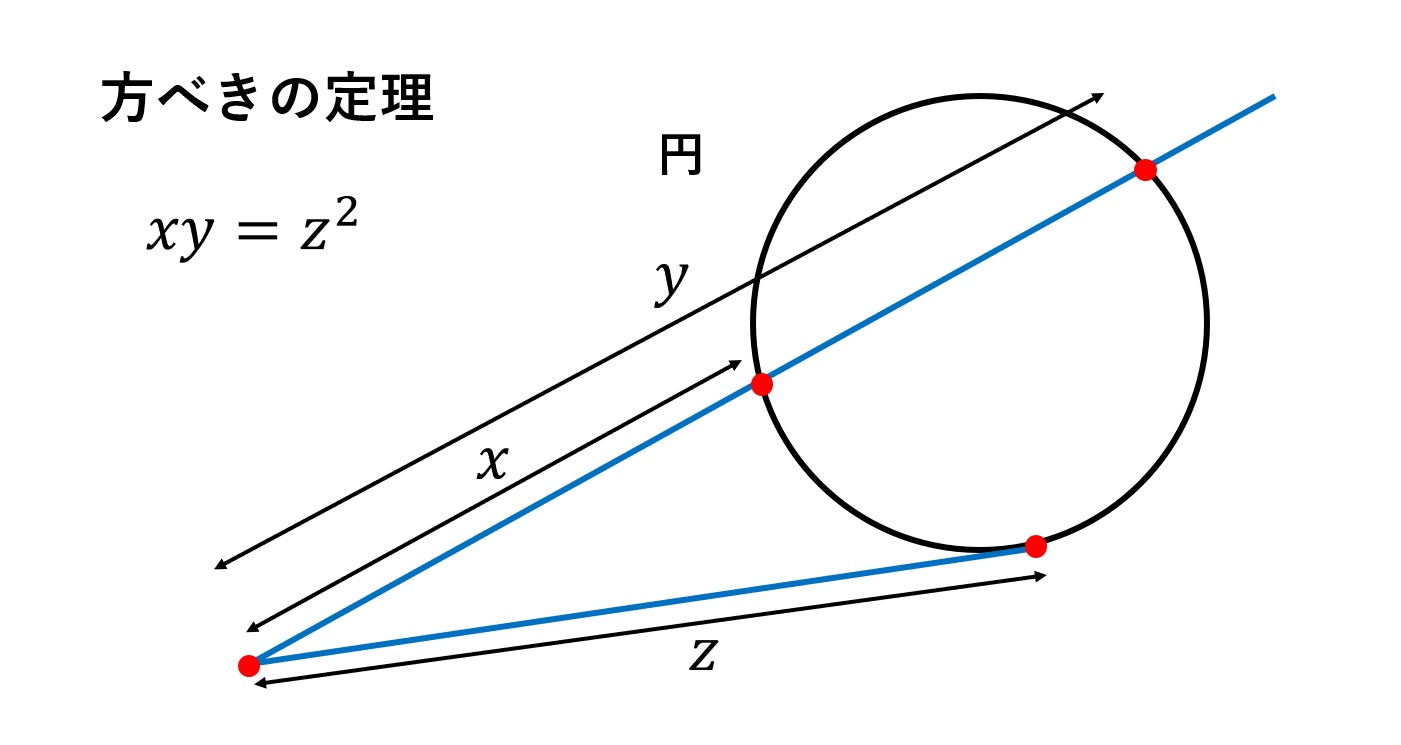
この事実を使って三平方の定理を証明してみましょう。まずは直角三角形ABCを用意します。ここで頂点Aを中心として、半径\(b\)の円を描きます。すると当然ですが、円は頂点Cを通ります。

このとき直線ABと円の交点をそれぞれ図のようにD,Eとおきます。すると線分BD\(=c-b\), 線分BE\(=c+b\)となることから、方べきの定理により

\begin{align*}(c-b)(c+b)=c^2-b^2=a^2\end{align*}

となり、見事に三平方に定理が示されました。今回もお見事です！

 

３．三平方の定理の証明その３

次にご紹介する証明はレオナルド・ダ・ヴィンチによるものと言われています。アーティスティックな証明をご覧ください。

まず直角三角形ABCの２つの辺の長さ\(a\)と\(b\)を一辺とする正方形（赤と青）を作り、図のように線でつないで「線対称な六角形」を作ります。

この六角形を対角線で二等分に分け、片方を裏返して、図のように貼り付けます。すると「原点対称な六角形」が出来上がります。この六角形の面積を図のように比べてみます。

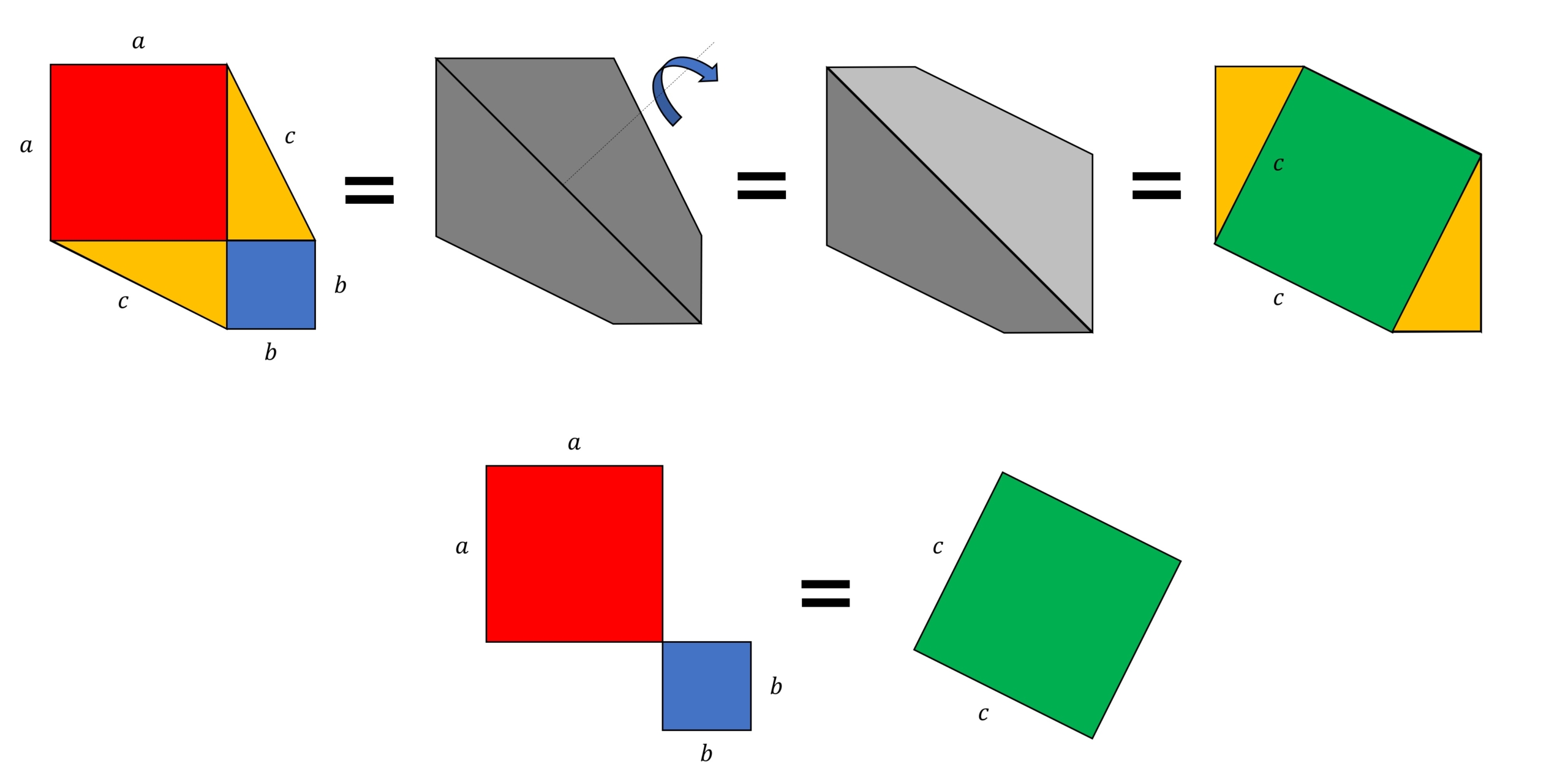
すると、直角三角形２個分（オレンジのエリア）は相殺され、三平方の定理\(a^2+b^2=c^2\)が自動的に導けています。スタイリッシュですね。。。！お見事です！！

 

４．三平方の定理の証明その４

次は言葉を使わない証明をいくつかご紹介いたします。言葉を使わないというのは、図で完結させるという、なんともクールな証明方法です。以下、ほとんど説明はいたしません。ごゆっくりご堪能ください。

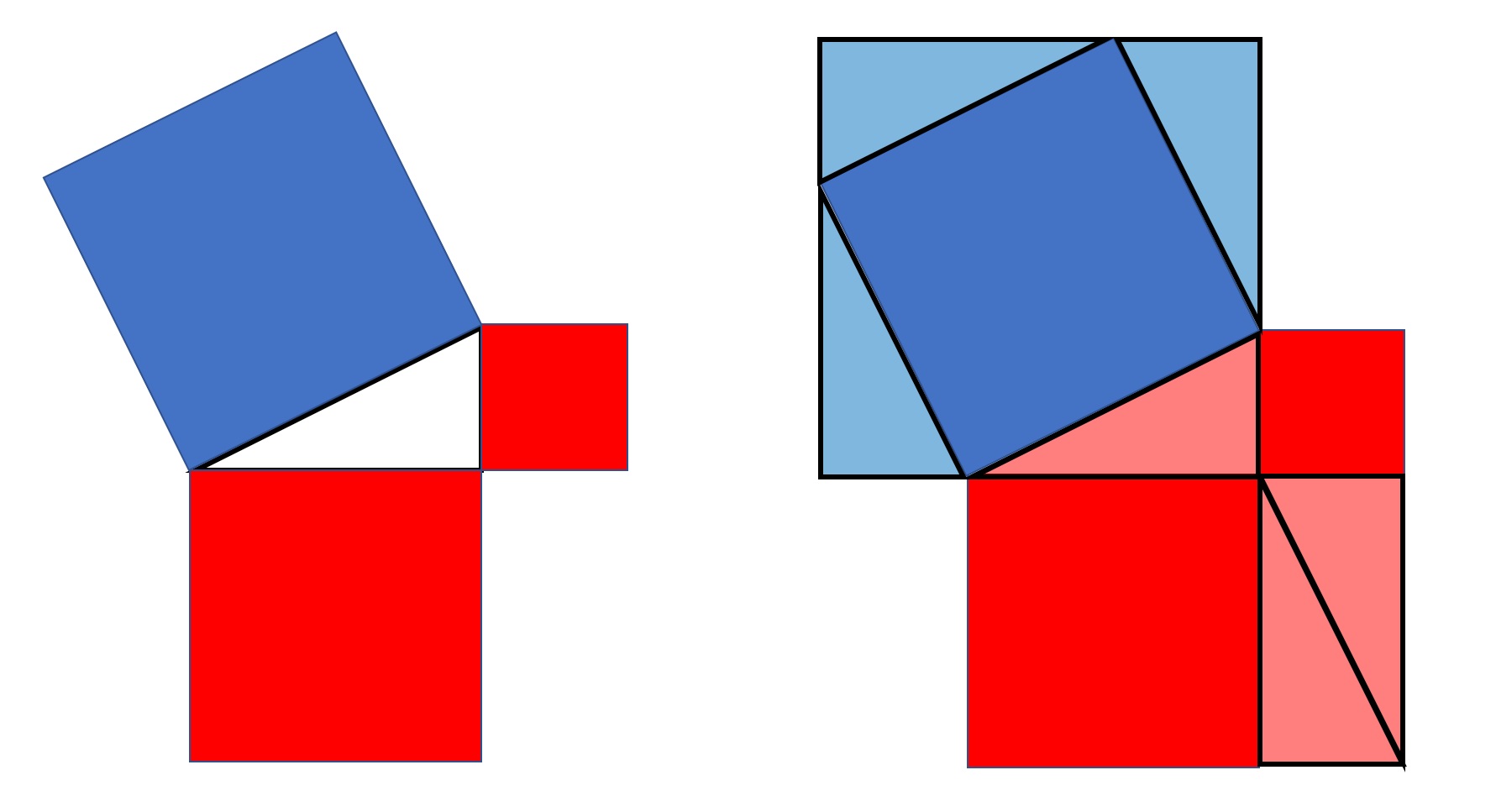
青の面積と赤の面積が同じであることにより三平方の定理が示されます！

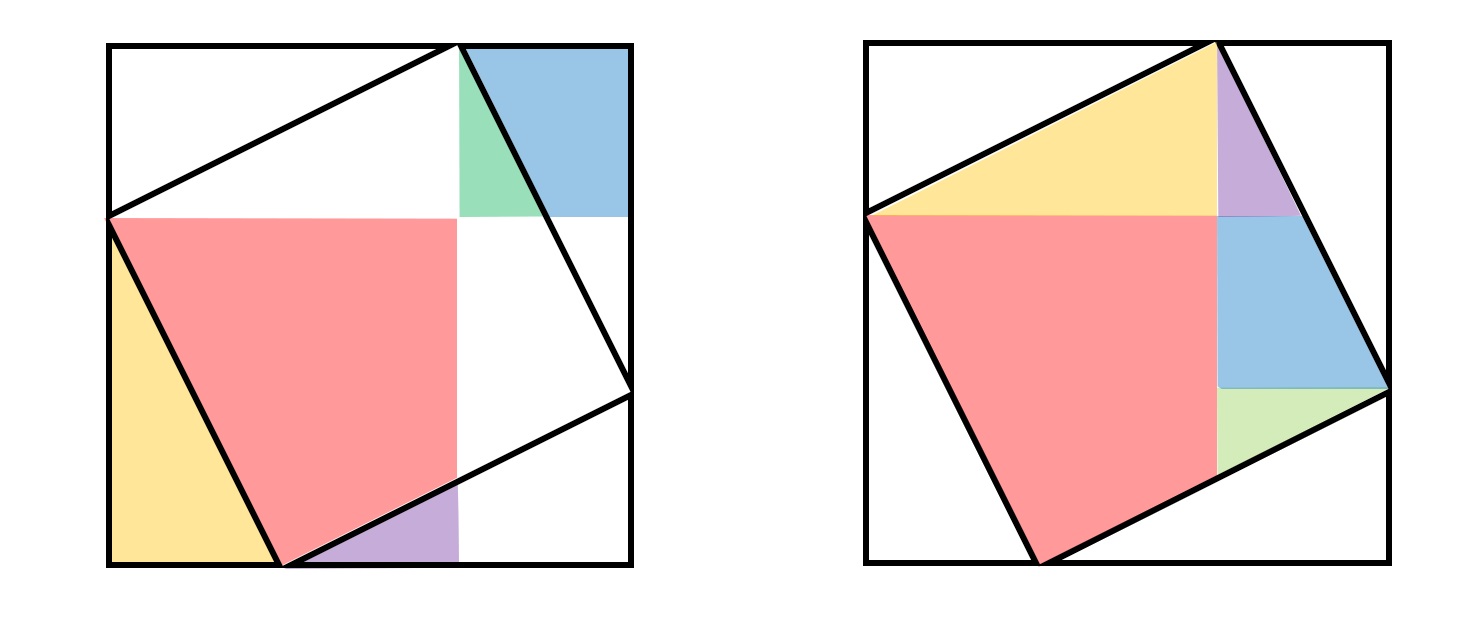
パズルのようにいじくることでいつの間にか三平方の定理が示せますね。。。

５．三平方の定理の証明その５

最後に究極の証明法をお見せしましょう。それがこちらです。

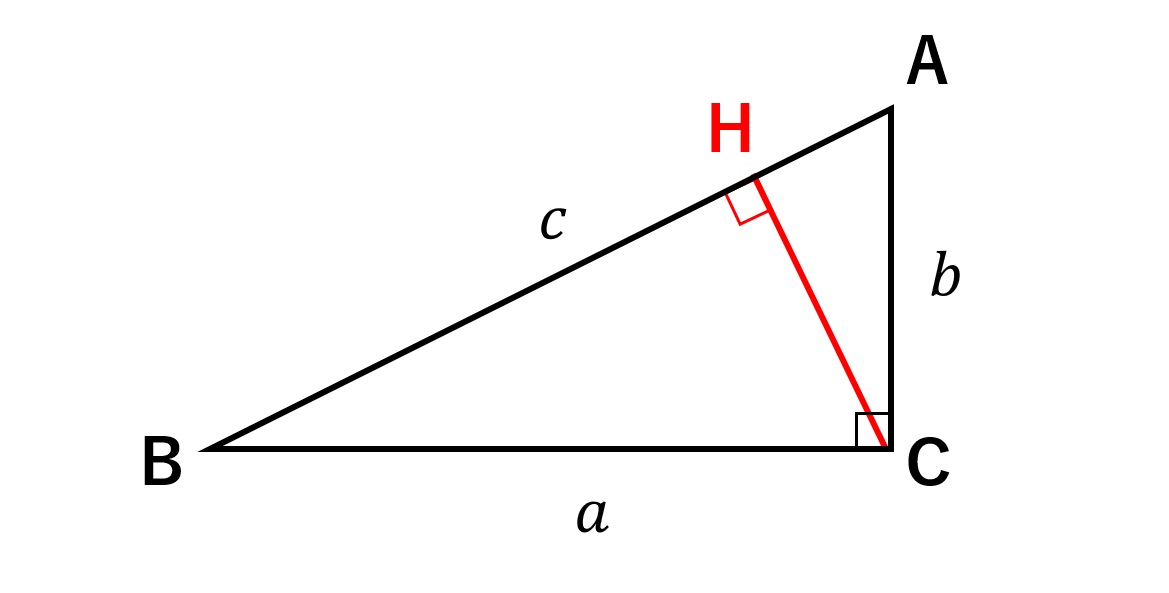
頂点Cから斜辺に向かって垂線を下ろしただけですが、実はこれで証明が完了しています。え！？って感じですよね。

少し解説を入れておきましょう。垂線の足をHとおきます。このとき、三角形ABC、三角形CBH、三角形ACHは全て相似な三角形であり、対応する辺の長さはそれぞれ\(c\),\(a\),\(b\)となります。

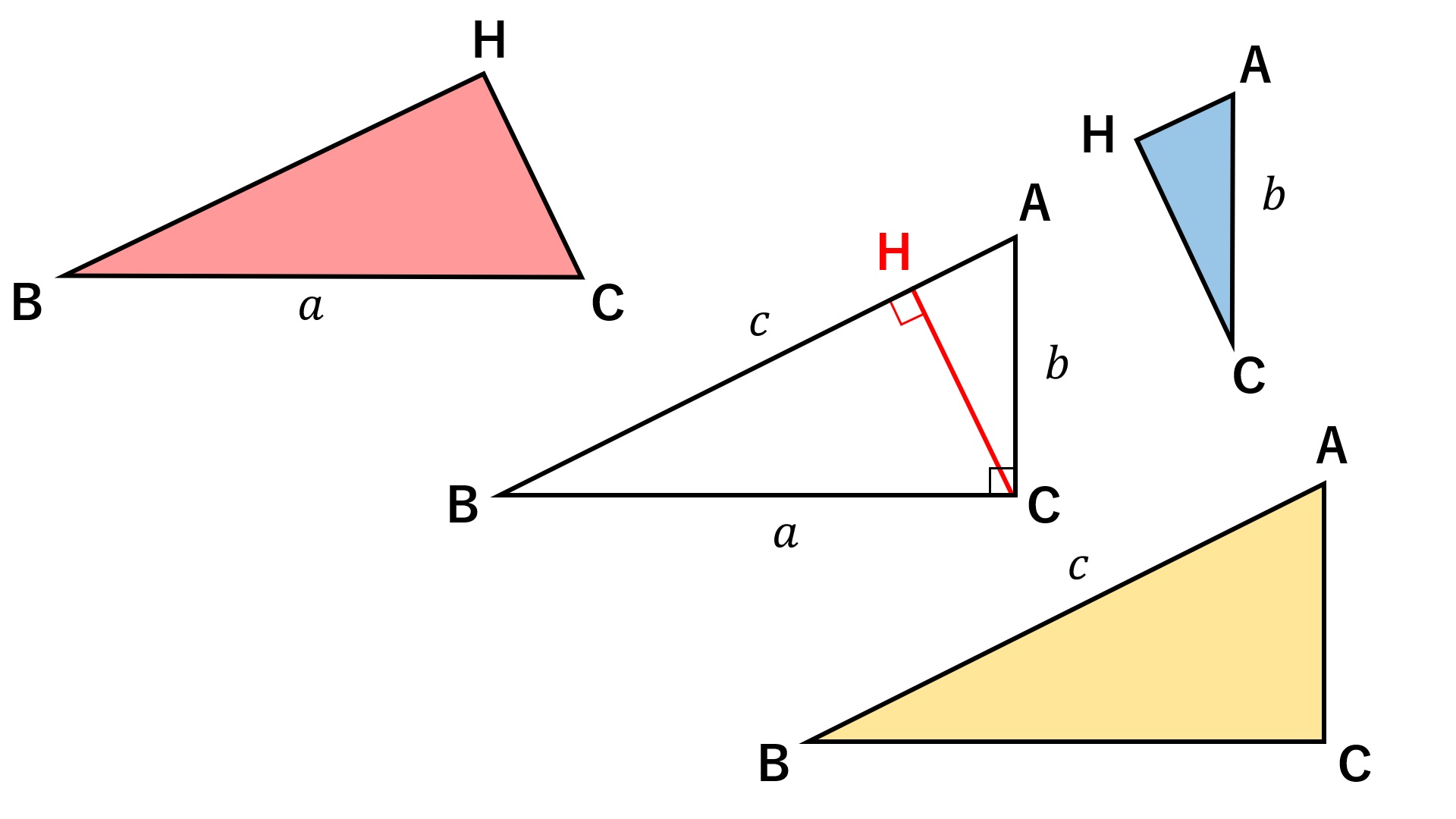
つまり面積比は\(c^2\):\(a^2\):\(b^2\)となり、これは三平方の定理

\begin{align*}c^2=a^2+b^2 \end{align*}

に他なりません。なんと鮮やかな証明でしょう、、、畏れすら感じます。。。

これらの証明を含めた100通り以上の証明がPythagorean Theorem で公開されています。興味のある方は是非ご覧ください。

６．さいごに

いかがでしたでしょうか。中学・高校で同じみであり、古代より伝わる幾何学の大定理の一つでもある「三平方の定理」。今日はその多様な証明方法をひたすらご紹介いたしました。

一つの定理にこれだけの証明のバリエーションがあるのは非常に興味深いですよね！いつか「素数の無限性」の美しい証明たちもまとめてみようと思います。

なお、今回ご紹介した三平方の定理の証明をもっと詳しく学びたい方は「ピタゴラスの定理 100の証明法 幾何の散歩道」をご覧ください。

また「言葉なしの証明」に関してはニールセンの「Proof without Words」という本があります。

また今回ご紹介した「証明」という手法としての美しさ。これは数学の一つの魅力だと思います。こうした「美しさ」やデザイン・アートに関する無料セミナーも開催しておりますので、興味のある方は是非ご参加ください。

数学的デザイン超入門

また、岡本の数学アート作品、デザイングッズはこちらから

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>