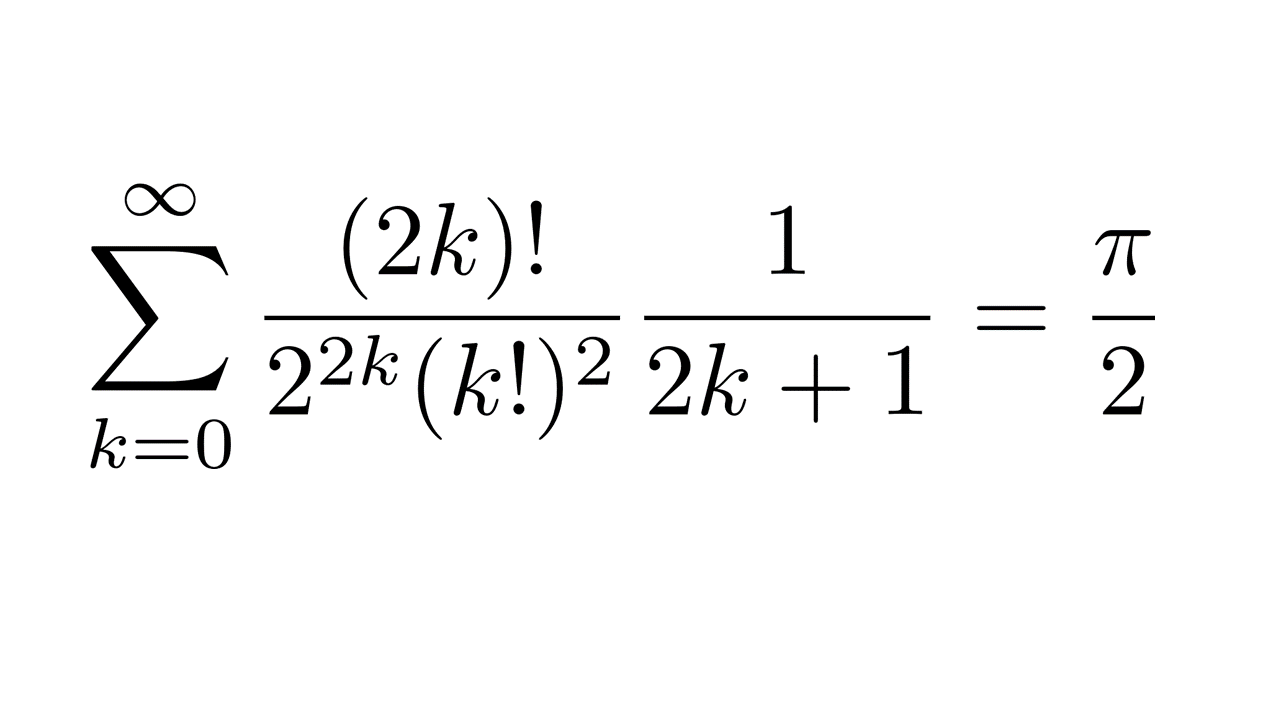
数学教室和(なごみ)講師の松中です。

本記事は、やばそうな数式の第三回の記事です。第一回の「意味編」、第二回の「総乗の証明編」は以下のリンクからお読みください。

やばそうな数式(意味編)～キラキラ数学プロジェクト～

やばそうな数式(総乗の証明編)～キラキラ数学プロジェクト～

今回は、やばそうな数式の総和の証明を行います。
$$\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} =\frac{\pi}{2}$$

「意味編」でお話しした通り、このやばそうな数式はネットで適当に見つけたもので、元々なぜ成り立つかはわかっていませんでした。自分で証明しようと試行錯誤し、総乗、積分は比較的早く証明ができたのですが、今回紹介する総和の証明はなかなか思いつきませんでした。ネットで調べようにもこういった数式はどう調べたらよいかわかりません。もちろんずっと考え続けていたわけではないですが、証明を思いつくまで1週間はかかかったと思います。

証明の難易度ですが、総乗が高校レベルであったのに対して、総和は大学一年(微積)レベルとなっております。

証明

証明のアイディア

まずは、証明すべき総和の式を眺めてみましょう。
$$\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} =\frac{\pi}{2}$$

自分が最初にこの式を見たときには、$\displaystyle \frac{(2k)!}{(k!)^2}$は$\displaystyle {2k \choose k}$であるということくらいしか思いつかず、$\displaystyle {2k \choose k}$に変形してもそれ以上変形の仕様がなく困り果てていました。しかし、一週間後くらいにふとしたタイミングでこれはテイラー展開ではないかとひらめきました。

関数$f(x)$の$x=0$でのテイラー展開は、
$$f(x)=\sum_{k=0}^\infty\frac{f^{(k)}(0)}{k!}x^k$$
で与えられます。これは複雑な関数を扱いやすいべき級数で表そうというものです。

このテイラー展開で$x=1$とすると、
$$f(1)=\sum_{k=0}^\infty\frac{f^{(k)}(0)}{k!}$$
となるので、これと証明したい式を見比べると、

・$\displaystyle f(1)=\frac{\pi}{2}$
・$\displaystyle f^{(k)}(0)=\frac{(2k)!}{2^{2k}k!} \frac{1}{2k+1}$

であるような関数$f(x)$を見つければ、証明できることが分かります。

数学好きであれば$f(1)$が$\frac{\pi}{2}$となる関数は$\sin^{-1}(x)$であるとすぐに思いつくでしょう。ネットで$\sin^{-1}(x)$のテイラー展開を調べると

$$\sin^{-1}{x}=\sum_{k=0}^\infty\frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1}x^{2k+1}$$
と出てきて、このテイラー展開には今回示したい式の形がそのまま入っているため、勝利を確信しました。証明は終わったも同然ですが、本記事では$\sin^{-1}{x}$のテイラー展開を導きます。

$\sin^{-1}{x}$のテイラー展開

$f(x)=\sin^{-1}{x}$をテイラー展開するために微分していきましょう。$\sin^{-1}{x}$は$\sin{x}$の逆関数であるため、逆関数の微分の公式
$$\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}$$
を使って、$\sin^{-1}{x}$を微分します。

$y=\sin^{-1}{x}$とおくと、$x=\sin{y}$ですから、
$$\frac{dx}{dy}=\cos{y}$$
です。よって、
$$\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{\cos{y}}$$
として、$\sin^{-1}{x}$を微分することができます。右辺が$y$の関数の形になっているため、$x$の形にする必要がありますが、$x=\sin{y}$であることと、$\cos^2{y}+\sin^2{y}=1$であることから、$\cos{y}=\sqrt{1-x^2}$が導け、
$$f^{\prime}(x)=\frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}}$$
がわかります。

$\sin^{-1}{x}$を微分すると、難しそうな三角関数の形が消えたので、あとはひたすら微分していけばよい気はしますが、これがなかなか難しいです。

後の数式を見やすくするため、ここでは$\displaystyle g(x)=f^{\prime}(x)=\frac{1}{\sqrt{1-x^2}}$と置きます。$\displaystyle g(x)=(1-x^2)^{-\frac{1}{2}}$であることに注意し、合成関数の微分の公式を用いて何度か微分してみましょう。
$$\begin{align*} g^{\prime}(x)&=-\frac{1}{2}(1-x^2)^{-\frac{3}{2}}\times(-2x)=x(1-x^2)^{-\frac{3}{2}}\\ g^{\prime\prime}(x)&=(1-x^2)^{-\frac{3}{2}}-\frac{3}{2}x(1-x^2)^{-\frac{5}{2}}\times(-2x)\\ &=(1-x^2)^{-\frac{3}{2}}+3x^2(1-x^2)^{-\frac{5}{2}}\\ g^{\prime\prime\prime}(x)&=-\frac{3}{2}(1-x^2)^{-\frac{5}{2}}\times(-2x)+6x(1-x^2)^{-\frac{5}{2}}\\ &-\frac{5}{2}\times 3x^2(1-x^2)^{-\frac{7}{2}}\times(-2x)\\ \end{align*}$$

これ以上は気が滅入りそうです。ここでは少し工夫して、$\displaystyle h(x)=\frac{1}{\sqrt{1-x}}=(1-x)^{-\frac{1}{2}}$をテイラー展開してみます。$h(x)$がテイラー展開できれば、$g(x)=h(x^2)$であることから$g(x)$のテイラー展開が手に入ります。また$f^{\prime}(x)=g(x)$だったので、$g(x)$のテイラー展開を項別に積分することで元々得たかった$f(x)$、つまり$\sin^{-1}{x}$のテイラー展開を求めることができます。

次のように、$h(x)$の微分は簡単にできます。

$$\begin{align*} h^{\prime}(x)&=-\frac{1}{2}(1-x)^{-\frac{3}{2}}\times(-1)=\frac{1}{2}(1-x)^{-\frac{3}{2}}\\ h^{\prime\prime}(x)&=-\frac{1}{2}\cdot\frac{3}{2}(1-x)^{-\frac{5}{2}}\times(-1)=\frac{1}{2}\cdot\frac{3}{2}(1-x)^{-\frac{5}{2}}\\ h^{\prime\prime\prime}(x)&=-\frac{1}{2}\cdot\frac{3}{2}\cdot\frac{5}{2}(1-x)^{-\frac{7}{2}}\times(-1)=\frac{1}{2}\cdot\frac{3}{2}\cdot\frac{5}{2}(1-x)^{-\frac{7}{2}} \end{align*}$$

これを続けていくと、$\displaystyle h^{(k)}(x)=\frac{1}{2}\cdot\frac{3}{2}\cdots\frac{2k-1}{2}(1-x)^{-\frac{2k+1}{2}}$であることが分かり、結局$h(x)$のテイラー展開は、
$$h(x)=1+\sum_{k=1}^\infty\frac{(2k-1)!!}{2^kk!}x^k$$
となります。

あとは順に$g(x)$、$f(x)$のテイラー展開を求めていきます。$g(x)=h(x^2)$より、$g(x)$のテイラー展開は、
$$g(x)=1+\sum_{k=1}^\infty\frac{(2k-1)!!}{2^kk!}x^{2k}$$
となり、また、$f^{\prime}(x)=g(x)$より、これを項別に積分して、
$$f(x)=x+\sum_{k=1}^\infty\frac{(2k-1)!!}{2^kk!(2k+1)}x^{2k+1}$$
であることがわかります。$f(0)=\sin^{-1}(0)=0$であることから項別積分した際に定数項は出てきません。

ここで、$\displaystyle (2k-1)!!$を別の形に変形します。

$(2k-1)!!$は例えば$k=10$であれば、
$$19!!=19\cdot 17\cdot 15\cdot 13\cdots 3\cdot 1$$
となりますが、これは、
$$19!!=\frac{20\cdot 19\cdot 18\cdot 17\cdot 16\cdot15\cdots 4\cdot 3\cdot 2\cdot 1}{20\cdot 18\cdot 16\cdot 14\cdots 4\cdot 2}$$
と変形できます。つまり、
$$19!!=\frac{20!}{20!!}$$
です。この考察から、
$$(2k-1)!!=\frac{(2k)!}{(2k)!!}$$
がわかります。しかも$(2k)!!=2^kk!$であることから、
$$f(x)=x+\sum_{k=1}^\infty\frac{(2k)!!}{2^{2k}(k!)^2(2k+1)}x^{2k+1}$$
となります。右辺の$\sum$の中の式は$k=0$とすると$x$になることから、最終的に$\sin^{-1}{x}$のテイラー展開は、
$$f(x)=\sin^{-1}(x)=\sum_{k=0}^\infty\frac{(2k)!!}{2^{2k}(k!)^2(2k+1)}x^{2k+1}$$
となることがわかります。

さあ、あとは$x=1$とするだけです。$x=1$を代入すると、今回求めたかった式を得ることができます。
$$\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} =\frac{\pi}{2}$$

まとめ

今回はやばそうな数式の総和の等式を証明しました。実は証明の中でいくつか厳密性を無視しているところがあります。
・$g(x)$は項別積分してもよいのか？
・$f(x)$のテイラー展開の収束半径は$1$だが$x=1$を代入してもよいのか？

今回はとりあえずの証明というところで上については解説していませんが、気になる方は解析学の教科書を見ながら証明してみてください。

さて、最後に残ったのは、積分の等式の証明です。この証明には大学2、3年生で学ぶ複素関数の積分が必要になります。お楽しみに！

<文/松中>