収束する無限級数とは？―呪術廻戦で学ぶ本格数学―

ロマンティック

公開日

2021年3月21日

更新日

2021年3月21日

動画で見たい方はこちら↓↓↓

こんにちは。和からの数学講師の岡本です。今回は、漫画、アニメで話題沸騰中の「呪術廻戦」に出てくる数学のキーワードについて掘り下げいこうと思います。

注）以降は、若干ではありますが、漫画2巻やTVアニメのネタバレを含むのでご注意ください！なお、本記事における漫画の見解は岡本個人の意見です。

この記事の主な内容

１“最強の男”五条悟とその術式

「呪術廻戦」とは、人間の負の感情から生まれる呪いや“呪霊”といわれる化け物を「呪術」を使って祓う、呪術師の闘いを描いたダーク・ファンタジー・バトル漫画で、日本だけでなく世界各国で話題となっており、あの「鬼滅の刃」を超えるのでは？とも言われるほどです。
さて、今回はその作中で“最強”といわれる、呪術師「五条悟」（五条先生）について焦点を当てていきます。漫画やアニメを観られた方はお気づきかもしれませんが、彼の繰り出す「技」には数学的な要素が見え隠れしています。例えば、彼の最初のバトルシーンである漏瑚戦では、「無下限術式」という「“無限”を現実世界に作り出す」技を繰り出していきます（かっこいい）。

この「無下限術式」とは「収束する無限級数を現実化する術式」という設定になっており、「収束する力」を順転術式「蒼（あお）」、「発散する力」を反転術式「赫（あか）」、そしてそれらを衝突させることで生まれる虚式「茈（むらさき）」という大技が3つ描かれています（かっこいい）。
今回は「蒼（あお）」と「赫（あか）」で使われる「収束」と「発散」について詳しく見ていきましょう。

２．収束、発散とは

数学における「収束」とは、何か点列（数列と考えても構いません）があり、この点が最終的にどこか特定の位置に限りなく近づくとき、点列は収束するといいます。例えば何か適当な空間（完備距離空間）を考え、その中を彷徨う点列を\(a_n\)と書くことにします。この点列が「限りなく\(\alpha\)に近づく」ということを、高校数学ででてくる記号を使って

\begin{align*}
\lim_{n\to \infty}a_n=\alpha
\end{align*}

と表現することができます。しかし、これではやや曖昧です。「限りなく」とは何でしょう？「近づく」とは何でしょう？と、考えてみればキリがありません。この部分を厳密に扱うために大学数学では「\(\varepsilon\)-\(N\)論法」という論法を使います。これについては、以前マスログで紹介しているので、こちらも併せてご覧ください（必見です）！

“限りなく近い”世界へ―ε-N論法への誘い―

さて、この「\(\varepsilon\)-\(N\)論法」を使うことで点列\(a_n\)が\(\alpha\)に「収束する」ことを以下のように表現できます。

\begin{align*}
\forall \varepsilon>0, \exists N\in \mathbb{N}　\text{ s.t. } n\geq N\Longrightarrow d(a_n, \alpha)<\varepsilon. \end{align*}

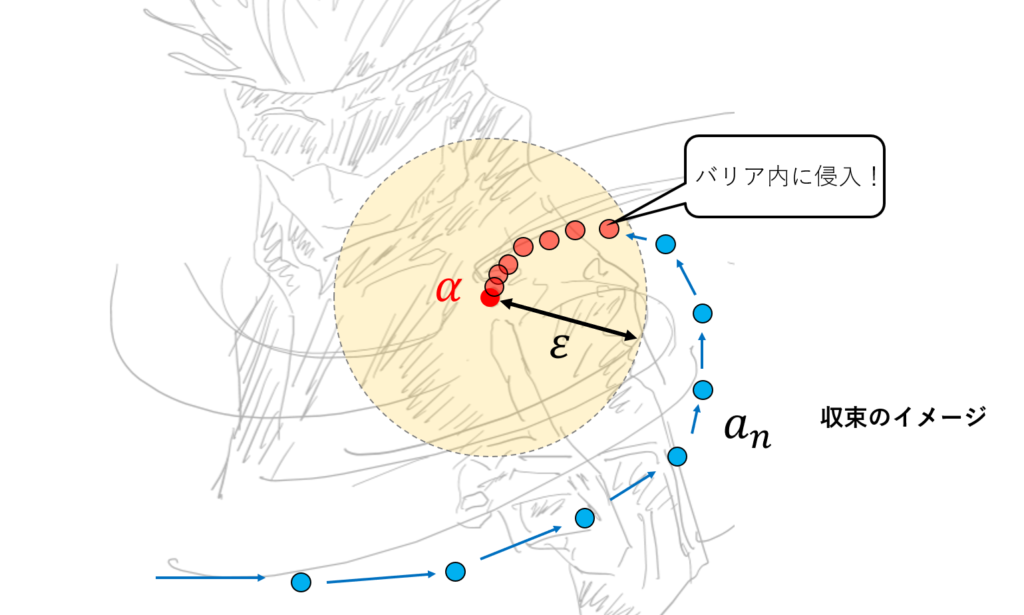
以前のマスログでは\(d\)の部分は絶対値\(||\)を使ってしますが、これは「距離関数」といって、点と点の距離を表しています（あまり気にしなくていいです）。つまり、「点\(\alpha\)の周りに、どんなに小さい半径\(\varepsilon\)のバリアを張っても、ある程度番号の大きい（具体的に\(N\)以上の番号の）\(a_n\)はバリア内に入り込んでくる」。これが「収束」の意味です。

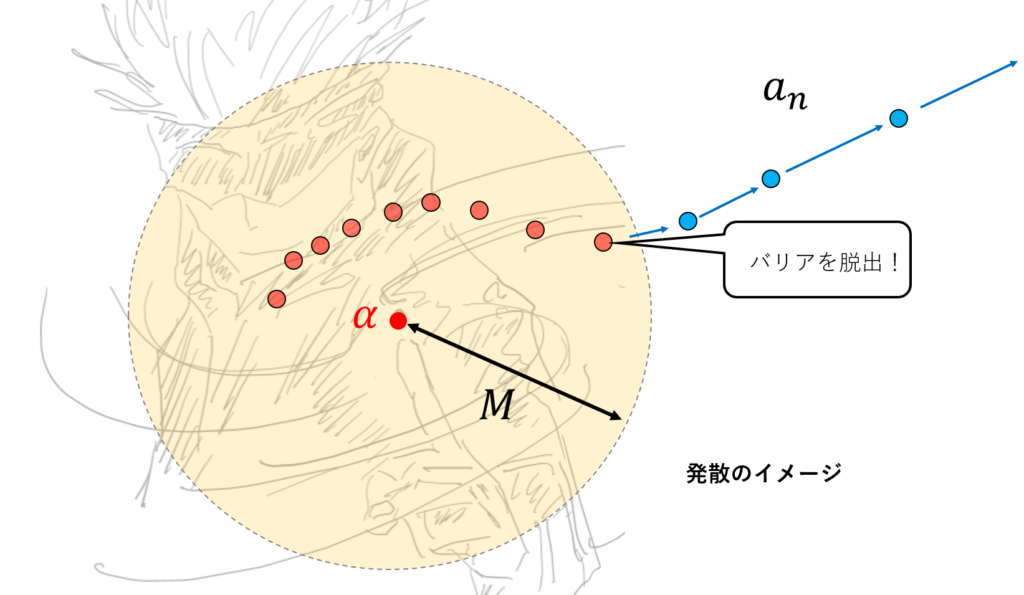
これを踏まえて「発散」というものを考えてみましょう。これは、適当に\(\alpha\)という基点を考え、番号を大きくするとこの位置から「いくらでも離れてしまう」という状況です。数式を用いて表現すると、

\begin{align*}
\forall M>0, \exists N\in \mathbb{N} \text{ s.t. } n\geq N\Longrightarrow d(a_n, \alpha)> M.
\end{align*}

つまり、「点\(\alpha\)の周りに、どれだけ大きな半径\(M\)のバリアを張っても、いつかこのバリアを脱出する番号\(N\)が存在する」。これが「発散」の意味です。

３．無限級数とは

次に「無限級数」について説明します。「無限級数」とは非常にシンプルに言うと、数列をずーっと足していったものです。どれだけ足していくかというと、「無限」に足していきます。一見、\(1+1+1+\cdots\)というように「数を無限に足す」という操作は、いくらでも大きくなる印象ですよね。まさに「発散」です。しかし、足していく数がどんどん小さくなっていく場合、いくら無限に足しても有限の値になることがあります。それが「収束する無限級数」なのです。次のような具体例を見ていきましょう。

\begin{align*}
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\cdots
\end{align*}

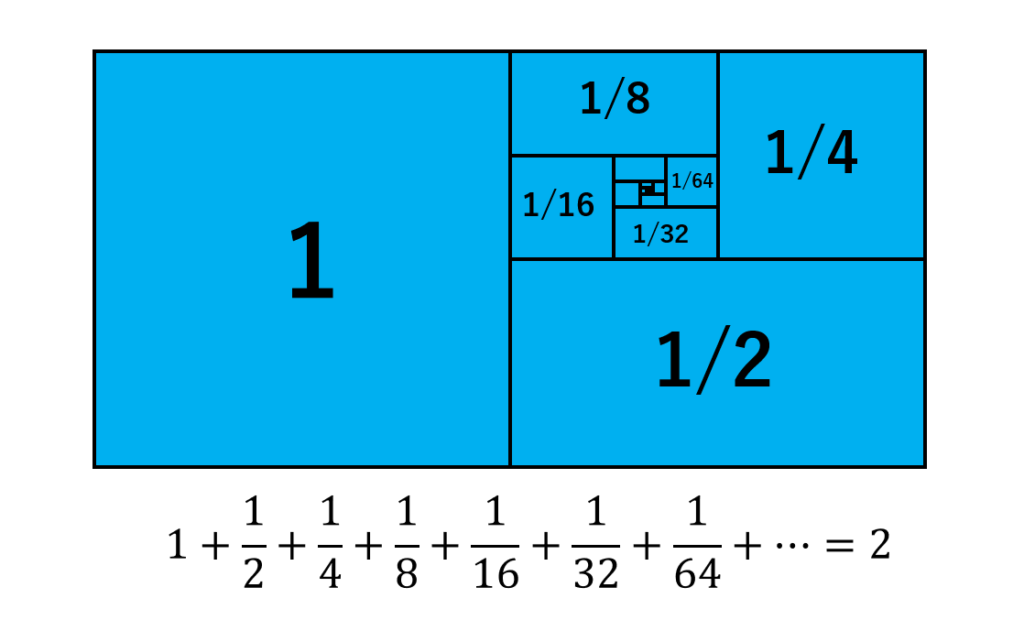
足していく数がどんどん「半分」になっていき、最終的にゼロに近づいていきます。この無限級数は「2」に収束します。例えば、以下の長方形のように、足し続けることで、1\(\times\)2の長方形の面積になることから説明できます。

では、足していく数がゼロに近づくような無限級数は全て収束するのでしょうか？答えはNoです。実は以下の無限級数は、無限大に発散することが知られています。

\begin{align*}
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots=\infty
\end{align*}

まさに「塵も積もれば山となる」現象です。たしかに足していく数\(\frac{1}{n}\)は0に近づいていますが、絶妙なラインで発散してしまいます。なお、0に向かうスピードが速い次のような無限級数は格別な値に収束することが知られています。

\begin{align*}
1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\cdots=\frac{\pi^2}{6}
\end{align*}

つまり、2乗であれば収束します。また、この累乗の部分を変数（虚数の世界までも考えられます！）として関数は「リーマン・ゼータ関数」と呼ばれ、未解決の懸賞金問題の一つである「リーマン予想」とも関係しています。

\begin{align*}
\zeta(s):=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\frac{1}{6^s}+\cdots
\end{align*}

４．無限級数の収束と発散、そして条件収束

与えられた無限級数が収束するか、発散するかを判別するための定理や命題はいくつか知られています。例えば、数列\(a_n\)の無限和

\begin{align*}
\sum_{n=1}^{\infty}a_n=a_1+a_2+a_3+a_4+\cdots
\end{align*}

について考えてみましょう。この無限和の各項\(a_n\)は正の値かもしれないし、負の値かもしれません。そこで、一律に正の値を取るように絶対値を付けた無限和は明らかに元の無限和よりも大きくなります。

\begin{align*}
\sum_{n=1}^{\infty}a_n\leq \sum_{n=1}^{\infty}|a_n|
\end{align*}

仮に絶対値を付けた無限和がある一定の値に収束する場合、もとの無限和も収束することが保証されます。このとき、無限級数\(\sum_{n=1}^{\infty}a_n\)は絶対収束するといいます。つまり、無限和が「絶対収束」すれば（＝絶対値を付けても無限和が収束すれば）、元の無限和も収束するのです。では、収束はするけれども、絶対収束しない例はあるのでしょうか？実はあります。例えば

\begin{align*}
1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-+\cdots=\log 2
\end{align*}

などの収束する無限級数は、絶対値を付けると3節の考察で現れた、「絶妙に」発散する無限和となります。このような正、負と交互に符号を変えていく級数を交代級数と呼び、収束はするが、絶対収束しない級数は条件収束するといいます。

そして、条件収束する無限級数についてはリーマンによる、次のような驚くべき定理が示されています。

定理（リーマン）
条件収束する級数は足し算の順番を変えることで任意の値に収束させたり、発散させることができる。

つまり、条件収束する無限級数は、足し方を調整するだけで、収束、発散をコントロールすることができるのです！！なんだか五条先生みたいですね…！

５．さいごに

いかがでしたでしょうか？今回は呪術廻戦の中で現れる数学的なキーワードについて掘り下げました。もちろん呪術廻戦は、五条先生の「無限」だけでなく様々な数学要素が詰まっています。独自の視点で捉え、数学も楽しめるとなると一石二鳥ですね！なお最後の紹介した定理の詳しい内容が知りたい方は杉浦先生の解析入門がオススメです。

基礎数学2 解析入門1 杉浦光夫(著) 東京大学出版会