※本記事はロマ数トレラン「数学的な基本原理から量子論を学ぶ」の講師である本田耕一郎先生による量子論の入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

始めに

20世紀の最初の四半世紀の間に,ミクロの世界に関する私たちの理解は根本的な変化を遂げてきた. 波動と考えられてきた光は光電効果やコンプトン効果の実験により粒子のようにも振る舞うことが明らかになった. 一方,粒子と考えられてきた電子は回折の実験より光と同様に波動性を持つことが明らかになった. これら光や電子など量子と呼ばれるミクロな対象は,波のような側面と粒子のような側面の二重性を持つことが本質的な特性であると考えられている.この「波―粒子」の二重性はニュートン力学とマクスウェルの電磁気学という古典論では記述できない現象である. そしてミクロの世界の物理を記述する一貫した理論として量子論が誕生した. ここでは前期量子論から,量子論として確立したシュレディンガーの波動力学,ハイゼンベルグの行列力学をかいつまんで紹介し最後に光の二重性を示す実験を紹介する.

前期量子論

前期量子論は1900年,プランクによる黒体放射(輻射)の理論(エネルギー量子仮説)により始まった. プランクは黒体内の放射場のエネルギーが振動数に比例した特定の値を単位としてしか変化できないという「量子化」の概念を提唱し, 振動数とエネルギーを結びつける定数(プランク定数)\(h\) を導入した. この仮定に基づいてプランクが導出した式は黒体放射の実験結果と一致した.
このエネルギーの量子仮説(量子化)はその後の量子力学の始まりに大きな影響を与えた.

プランクに続き, アインシュタインが量子化の概念を光に拡張し, 光電効果を説明するために光量子仮説を提唱した. 光量子仮説に従えば振動数\(\nu\)の光は電磁波(波動)であると同時に\(E=h\nu\)というエネルギーを持つ粒子として振る舞う. この考え方は放射場のエネルギー変化を不連続としたプランクの概念を他の系に拡張するものである.

1923年にコンプトンはX線を物体に照射したとき,散乱X線の波長が入射X線の波長より長くなる現象を見出した(コンプトン効果). コンプトンは光のエネルギー\(h\nu\), 運動量\(h\nu/c\)を持つ粒子と考えて鮮やかに説明した. これは光の粒子性を最も顕著に示す証拠である. 運動量やエネルギーのような物理量を媒介するものとしての電磁波(光)を光量子(または光子)と呼ぶ.

ボーアはこれまで輻射や光の量子条件に関係する理論であった量子仮説を, 原子の構造を記述する理論に適用し,いわゆる前期量子論を打ち立てた. それまでに正電荷を持った重い原子核の周りを電子が回っているというラザフォードの原子模型があり,これによって原子による\(\alpha\)線の散乱が定量的に説明されていた.

しかし幾つかの問題があった.一つは原子核の周りをまわっている電子は常に加速されているため古典電磁気学によるとそのエネルギーを次第に失い,短い時間に原子核へ落ち込んで原子が不安定になるはずである.しかし原子の大きさは一定で安定である.もう一つは原子から放出される光のスペクトルに関するもので,このモデルでは電子の軌道が小さくなるはずだから電子の運動周期が短くなり,出てくる光の振動数は連続的に変化するはずであるがこれは実験と矛盾する.

1885年にバルマーは水素原子からの可視光のスペクトル線の間に離散的な関係があることを見出した.これらは古典論では理解できない. これら二つの困難を解消するために考案されたのがボーアの原子模型である. ボーアはここで二つの仮説を立てる.

ボーアの模型は,なぜ円運動する電子がエネルギーを失わないか, という点を説明するものではないが,量子条件仮説により水素原子に関する実験結果を見事に説明した. またこれにより原子の殻構造から元素の周期律の解明に見通し与えた.
　　

量子論の始まり

ルイ・ド・ブロイは, 光が波動性質とともに粒子としての性質を持つという二重性が, 電子のような粒子に対しても成り立つのではないかと考えた.つまり粒子である電子に対しても波長と振動数が定義できて, 波動としての振る舞いをするのではないかという物質波(ド・ブロイ波)の考えを提案した(1924〜25年). この考えは電子線の金属結晶による回折現象により実証された.

波動力学の成立

1926年にエルヴィン・シュレディンガーは電子が従うべき波動方程式を導き,シュレディンガー方程式と対応づけた. このシュレディンガー方程式は,水素原子の離散的なエネルギー準位を上手く説明することに成功した.これによって記述される電子の運動力学が波動力学である.

波束からシュレディンガー方程式へ

波束(wave packet)は局所的に存在する波動であり,移動する1個の波動の塊のようにふるまう.

この波束は波数の異なる多数の正弦波の重ね合わせで構成できる(合成波). つまり多くの波が規則的に重ね合わされて,空間のある1点の近傍にのみ波が残る.

　　
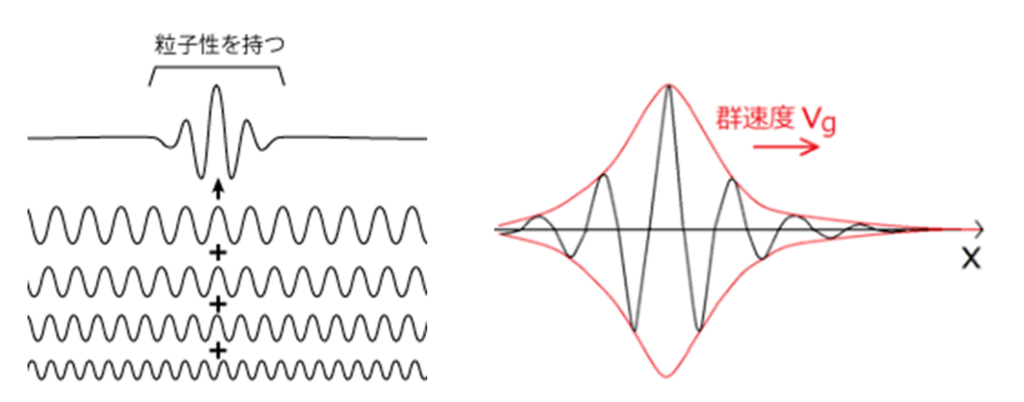
この場合,よりサイズの小さい波束を得るには,より多くの波を重ねる必要がある.一次元で考えると,一般に波束は次のように正弦波の重ね合わせとして表される.

\[
\psi(x,t)=\frac{1}{\sqrt{2}}\int_{-\infty}^{\infty} A(k)e^{i[kx-\omega(k)t]}dk
\]

この波束の重心が質量\(m\), 運動量\(p\)の古典粒子のように運動すると考えると,この粒子は運動エネルギー\(E=p^2/2m\)を持っている.粒子の速度\(V=p/m\)は波束の群速度\(V_g=d\omega/dk\)と同じとみなせるから\(dω/dk=p/m\)となる. アインシュタインの関係\(E=h\nu\)が粒子の場合にも成立すると仮定すると\(\omega = p^2/2m\hbar\). これらが成立するためには\(p=\hbar k=h/\lambda\)(ド・ブロイの関係)が成立する必要がある. \(\omega(k)=\hbar p^2/2m\)として波束の表式を\(p\)で書き換えて時間\(t\)で一回微分した式と位置座標\(x\)で二回微分した式を比較するとシュレディンガー方程式が得られる.

この微分方程式の解を波動関数とすると,この方程式は1)\(\psi\)に対して線形で重ね合わせの原理を満たし,2)時刻\(t=0\)での波動関数の値が分かればその後の任意の時刻での波動関数が求められる.ポテンシャルエネルギー\(V\)が存在する一般の場合にも1),2)を満たすことが要求される.

一般のシュレディンガー方程式は
\[
i\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}+V\psi
\]
となる.

波動関数とボルンの確率解釈

シュレディンガーは当初,粒子が雲のように広がりその密度が波動関数の絶対値の二乗\(|\psi|^2\)で与えられる実在波の立場をとった.しかしながら実験によれば電子はいつも粒子として観察され,一個の電子の密度が空間的に広がって見出されることは決してない.このことを考慮してボルンは波動関数の絶対値の二乗が電子の存在確率を表すものとの意味づけを行った 量子力学では粒子はあくまで粒子として考え波動関数は粒子の統計的振る舞いを定めるものと考える.

不確定性関係

位置と運動量のあいまいさの積により不確定性の関係が得られる
\(\psi(x,0)= A(k)\exp{(-ikx_0)}\exp{(-x^2/\Delta^2)}\)の形とすると\(\psi(x,0)\)は\(x=0\)で極大になり\(x= ±\Delta\)で\(1/e\)に減衰する.その広がり幅\(\Delta x\)は\(\Delta\)程度と考えられる.一方\(A(k)=A\Delta \exp{(-(k-k_0)^2\Delta^2)}\)とすると\(k\sim k_0\)で極大で\(k＝k_0±1/\Delta\)で\(1/e\)に減衰する.したがって広がり幅\(\Delta k\)は\(1/\Delta\)程度になる.したがって二つの幅の績\(\Delta x\cdot \Delta k \sim 1\)となり両辺に\(\hbar\)をかけてド・ブロイの関係より\(\Delta x\cdot\Delta p \sim \hbar\)の関係が成立していることがわかる. 一般の波束に関しては\(\Delta x \cdot \Delta p \geq \hbar\)としてよい.

行列力学

さてシュレディンガーとほぼ同時期に1925 年,ハイゼンベルク(当時23歳でゲッティンゲン大学講師)は,ボーアの原子模型を突き詰める形で,古典的な物理描像を捨て新しい量子力学の理論の定式化を行った.行列力学を確立した.

ハイゼンベルグは物理量の連続的な時間発展という古典力学の基本的な考えを放棄した.そしてすべての量子論的物理量は定常状態の量子数の組\((n,m)\)に関連する,一般には無数の複素数の集まりによって置き換えられると考えた.二つの整数\((n,m)\)に依存する数の集まりとは行列の概念に対応する. 行列力学では運動量や位置などの物理量を行列により表現し,現象をいわゆるハイゼンベルクの運動方程式で記述した. ところで行列においては二つの行列の績の非可換性が問題となる.行列力学が明らかにした物理量の非可換性は,量子力学における不確定性関係の構造を明らかにした.古典力学では運動量や位置はある時点においては確定した(決定論的)値を持つが,量子力学では物理量の非可換性により,例えば運動量と位置とは同時に確定値を取れない.

波動力学と行列力学の関係

波動力学と行列力学とは数学的に同等であることがシュレディンガーによって証明された.行列力学は量子論をハイゼンベルク描像により行列表示で定式化し,波動力学は量子論をシュレディンガー描像で位置表示の波動関数で定式化したものである.

量子論の基本原理(すべての量子論に共通な根本原理）

ひとつの物理状態に\(\psi\)という名前を付けたとする．

実験によると,ひとつの物理量\(A\)を同じ\(\psi\)について測定すると，測定値\(a\)は測定の度にばらつくが,同じ\(\psi\)を用意しては\(A\)を測定することを繰り返して求めた測定値の確率分布は定まる.

別の状態について測れば確率分布は変わる. 同じ状態でも測る物理量を変えれば変わる.
つまり確率分布は\(\psi\)と\(A\)に依存する量，つまり\(\psi\)と\(A\)の関数である．

\(A\)の測定値がばらつかず同じ値になる状態もあるが，その場合は必ず他の何かの物理量の測定値がばらつく．全ての物理量が確定値をもつような状態は存在しない．

量子論(広い意味での量子力学)は，これらは自然の本性であるという立場をとり，定まっている部分である確率分布を\(\psi\)と\(A\)の関数として計算する理論体系として定式化された.

二重スリットの実験

ここで光が粒子性と波動性を併せ持つ量子であることを示す決定的で美しい実験結果を紹介する. これによると複スリットを用いたヤングの干渉実験において,光を弱くして「光が一粒しかない状態」でも,一粒の光子が干渉縞を示すことが確認された.

「単一フォトンによるヤングの干渉実験」（浜松ホトニクス／1982年）

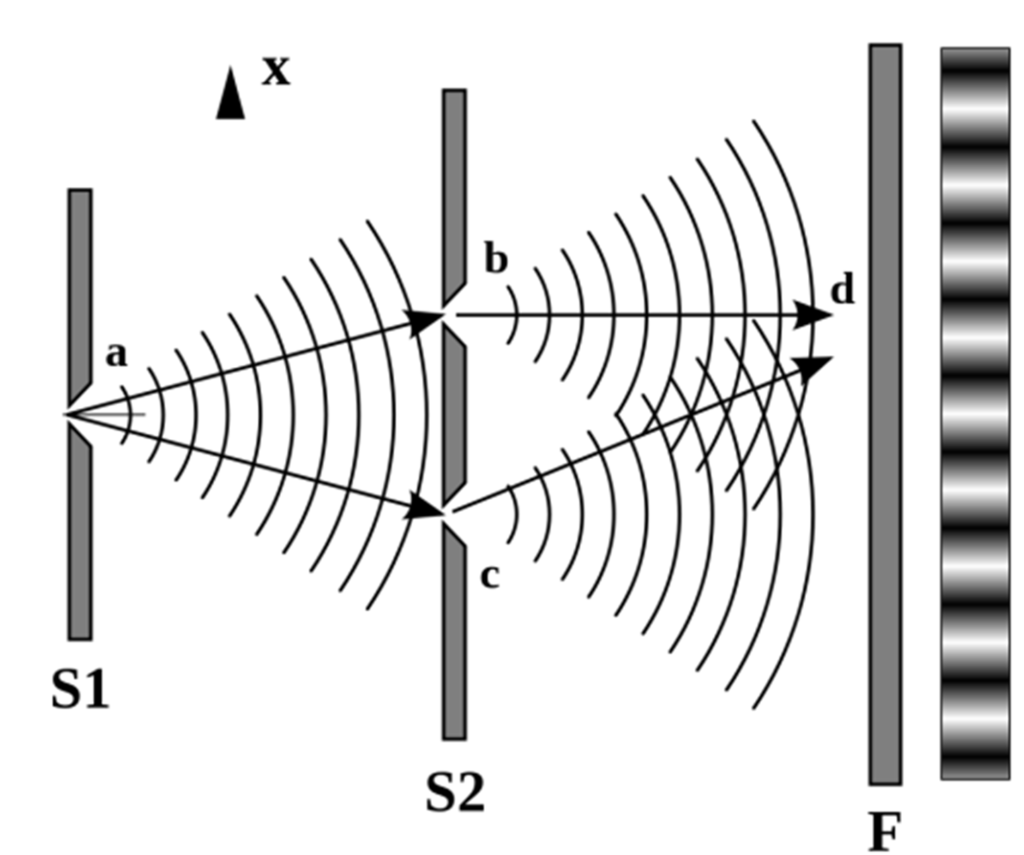
スリット間の間隔を\(a\), スリットとスクリーンの間の距離を\(D\), 光源の波長を\(\lambda\)とすると
光が強めあう条件は次のように表すことができる.
\[
x=\frac{nD\lambda}{a}
\]
\(x\)は上の条件を満たしたときに明るい帯ができる位置で,スクリーン上での縞模様の中心からの距離. \(n\)は任意の整数で, \(n=0\)は縞模様の中心を表す.

極限まで明るさを絞った光をスクリーン上で検出すると”粒”としてふるまう（左）一方,記録された”粒”の数が増えると干渉縞が姿を現す（右）.これにより光が”波”としてもふるまうことがわかる.

スリットの一つを閉じ,一粒の光子が片方のスリットだけを通るようにすると干渉縞が現れない.

この二重スリットの干渉実験では, 一粒の光子があたかも二つのスリットを同時に通過して,それ自身で干渉したということを示している.
量子力学的に解釈すると,スクリーン上での光子の存在をあらわす波動関数\(\psi\)は,重ね合わせの原理よりスリットを通過した場合の\(\psi_1\)ともう一方の\(\psi_2\)の和となり,どちらのスリットも同等とすると\(\psi = \psi_1＋\psi_2\)となる.したがってスクリーン上での光子の存在確率\(|\psi|^2\)は,\(|\psi_1|^2\)と\(|\psi_2|^2\)の和だけでなく\(\psi_1\)と\(\psi_2\)の交叉項が含まれる.これが干渉縞として現れる.一方のスクリーンを閉じると\(\psi\)には\(\psi_1\)か\(\psi_2\)しか含まれないため干渉縞は現れない.
この実験で単位量子であっても粒子性と波動性の二重性を示すことが実証された. 　

最後に

量子力学によるとミクロな状態の重ね合わせによる干渉や量子もつれといわれる現象が生じることが示されるが,これは現在注目されている量子通信や量子コンピュータに利用されている. 従って量子論はミクロな現象の理解に不可欠で,物理現象の本質を理解するうえでも実用上でも有用であると考えられる.

<文/本田耕一郎>