トポロジーって何?~ポアンカレ予想への招待~
公開日
2020年8月9日
更新日
2020年8月9日

※本記事はロマ数トレラン「ポアンカレ予想のはじまり-基本群を学ぼう-」の講師である佐々木和美先生によるポアンカレ予想の入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。
この記事の主な内容
隠れ正方形問題は難しい
1911年に Otto Toeplitzが発表した予想で、次のような未解決問題があります(詳細はこちら)。
「平面上の任意の単純閉曲線(※1)には、隠れ正方形がある(4点をうまく選べば正方形が張れる)」
日常の場面に言い換えるとこうなります。
「曲がりくねった道が最終的に元の地点に戻ってくるとすると、この道のどこか4カ所をうまく選んで杭を打ちロープを張れば、必ず正方形が作れる」
そのためこの問題は ” the Square Peg Problem (正方形の杭問題)” とも呼ばれています。
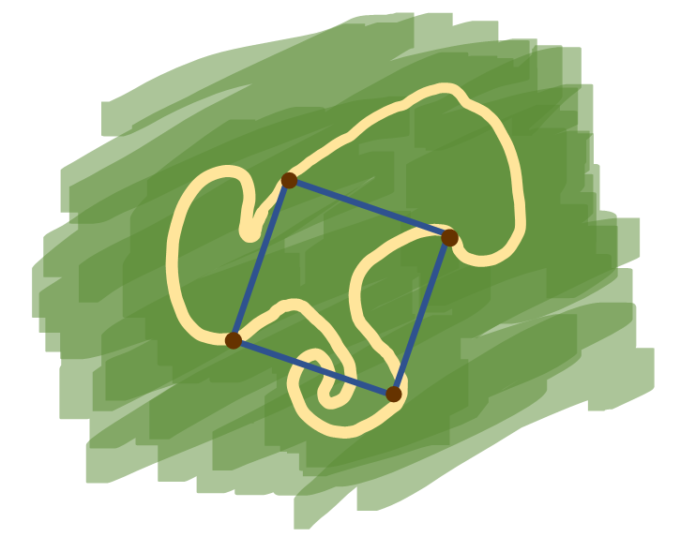
この問題の難しいところは、任意の「連続な」曲線を相手にしているところです。「(区分的に)微分可能な」場合、つまり、「なめらかな曲線のつぎはぎ」については、10年もたたないうちに予想が正しいことが証明されました(※2)。
https://arxiv.org/abs/2005.09193
そのほか、「凸曲線」など「性質のよい」タイプの曲線については証明が進んでいますが、「任意の連続な」曲線についての成否は、予想から100年以上たつ今なお未解決なのです(Inscribed square problem(wikipedia))。
連続だけど微分可能でない曲線
「区分的に微分可能」でOKなら、どんな曲線でもOKなのでは? と思うかもしれません。「すべての点で連続」だけど、「細かく分けても微分できない」ような曲線なんてあるの?
と。それがあるのです。例えば、カントール関数(悪魔の階段)とか、フラクタル曲線などです。
カントール関数(悪魔の階段)
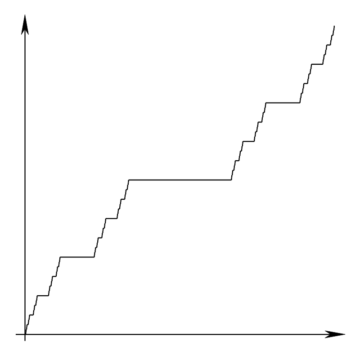
https://en.wikipedia.org/wiki/Cantor_functionより
フラクタル曲線
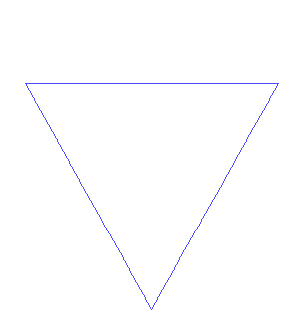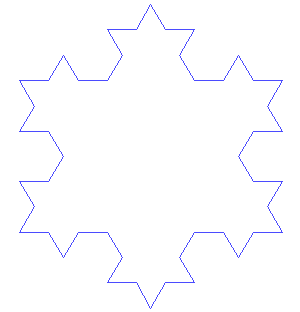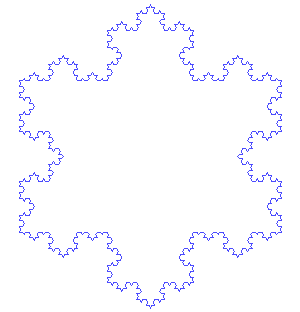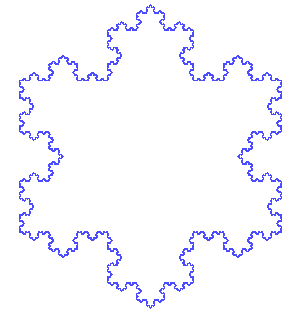
https://en.wikipedia.org/wiki/Koch_snowflakeより
一般の曲線を微分可能な曲線で近似しておいて、正方形を作り、だんだん近似の精度を上げて近づけて行って極限をとればいいのでは? と思う方もいるかもしれません。鋭いです。でも、それだと最終的に正方形が潰れて退化してしまう可能性を排除できないのです。
隠れ長方形問題はトポロジーで解ける
そこで、この超難しい問題をほんの少し簡単にした次のような問題を考えてみます。
「平面上の任意の単純閉曲線には、隠れ『長方形』がある(4点をうまく選べば長方形が張れる)」
『正方形』を『長方形』にしましたが、これだって、「任意の」(とてつもなく変な形かもしれない)単純閉曲線を相手にしているのですから難問です。ところが、トポロジーを使えば、いとも簡単に(?)その証明ができてしまうというから不思議です。
(以下の動画内の証明はH. Vaughan, Rectangles and simple closed curves,Lecture, Univ. of Ill. at Urbana, 1977(?). にもとづいています。)
具体的には「『メビウスの帯』の境界をすべて円周に貼り付けたら、3次元空間内ではどうしても自己交叉ができる(※3)」ということを使って証明できます。
https://www.quora.com/How-do-I-prove-that-the-projective-plane-cannot-embed-into-the-3-dimensional-Euclidean-space
円盤の縁にメビウスの帯の縁をすべて貼り付けたら……? 図のようになります。

(https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Boy_Surface-animation-small.gif より ©A13ean)
トポロジーとは
ここで「トポロジー “ topology ”」という言葉が出てきました。「位相(※4)」あるいは「位相幾何学」と訳されます。「位相」とは、集合の構造で「つながり具合」のこと。具体的には各点の「近傍系」を指定することで定まります。同時に、「位相」を研究する学問分野も「トポロジー」と言います。
また最近では「微分トポロジー」や「幾何学的トポロジー」が主流となってきました。これを日本語に訳したら「幾何学的位相幾何学」なんてことになって、さらに訳が分からないかも……。
ちなみに「幾何学」は英語で「ジオメトリー ” geometry ”」 です。「ジオメトリー」では長さや角度、面積、曲率などを用いて図形を研究するのに対して、「トポロジー」で扱うのはなんと「つながり方」だけ。「コーヒーカップとドーナツを同じとみなす」という話を聞いたことのある方もおられるでしょう。「つながり方」だけを見れば、そう、これらは同じ(位相同型)なのです。
「状態の空間」を表す「多様体」
初期のトポロジーは、これも約100年前、アンリ・ポアンカレ(1854-1912)が3体問題の研究をしていた中で生まれてきました。(※5)
・円平面制限3体問題では、円軌道を描く太陽と木星が固定される(回転している)座標系をとることができる。
・第3の惑星の位置と速度をあらわす「状態の空間」は2+2=4次元である。
・この運動には、エネルギーに対応するヤコービの積分という不変量があり、「状態の空間」の次元は、3である。
・3次元の「多様体」上のフローを研究すれば、円平面制限3体問題が理解できるはずだ。
数学を創る-数学者達の挑戦(学術俯瞰講義)2009年度開講
第12回 形の見分け方と数学の視点
坪井俊
https://ocw.u-tokyo.ac.jp/lecture_769/
ポアンカレは、「状態の空間」を一般化した「多様体(manifold)」(※6)というものを考えました。「多様体」とは、各点の近くだけを見れば、「線」「面」「3次元空間」など、ある特定の次元のユークリッド空間(\(\mathbb{R}^n\))の一部とみなせる図形(空間)を指して言います。
1次元多様体の例
具体的には、「1次元多様体」とは、局所的にはどこでも「線の一部」とみなせる図形です。全体の様子は問いません。曲がっていたり、輪になっていてもよいし、2つの部分からなる、というのもアリです。ただし、「枝分かれ」は許されません。ですから、文字で言えば、「い」「う」「し」「C」「D」「Z」なんかは1次元多様体ですが、「あ」「か」「B」「Y」などは多様体ではありません。
さらに、これらの「文字多様体」を「位相的な」観点だけで分類する(「位相多様体」とみなす)と、次のように分類できます。
| 多様体ではない | 線が2本 | 線が1本 | 閉じている |
|---|---|---|---|
| 「あ」「か」「B」「Y」 | 「い」「う」 | 「し」「C」「Z」 | 「D」「O」 |
「つながり方」だけに注目して分類していることに注意して下さい。
多様体の次元、閉多様体とは
また「多様体」の概念は、それが置かれた外側の空間は考慮していません。「多様体」それ自体が全体空間なのです。例えば、「バネ」は3次元空間内の図形ですが、局所的には「線」なので「1次元の多様体(1次元図形)」です。また、膨らんだビーチボール(中空)は、局所的には「面」なので、「2次元の多様体(2次元の図形)」です。3次元空間に浮かんでいるからといって、これらを「立体図形(3次元図形)」とは呼びません。これが高校までの数学とは違うところです。
多様体の「次元」とは、その多様体の外側の空間の次元とは一切関係なく、局所的な「つながり方(広がり方)」の次元を表していることに注意して下さい。「位相多様体」の観点では、「C」、「ばね」、「シャーペンの芯」はすべて同じです。
また、「多様体が閉じている」とか「閉多様体」とは、「コンパクトで境界がない」という意味であり、「閉集合」という意味ではありません。
「コンパクト」というのも数学用語ですが、平たく言えば「どんなにがんばってもいつまでも辿り漬けないような場所はない」ということです。(コンパクト空間(wikipedia))
さらに「微分可能性」も考慮した「可微分多様体(滑らかな多様体)」、多様体上の各点で長さや角度などが測れるようにした「リーマン多様体」などもあります。上の「文字多様体」の例では、「Z」「D」は「位相多様体」ですが、「可微分多様体」ではありません。
このような「多様体」がトポロジーの主な研究対象となります。
オイラー標数
さて、ポアンカレは、「3次元多様体」を分類しようと考えました。それまでに「2次元多様体」はすべて分類されていたので、それをさらに発展させようとしたのです。
「2次元多様体」、つまり「曲面」の「位相多様体」は、すでにオイラー標数(wikipedia)ですべて分類できていました。
オイラー標数とは中学校で習う次の定理の一般化です。
どんな多面体\(K\)でも、
「オイラー標数\(\chi(K)=\)頂点の数(\(V\))\(-\)辺の数(\(E\))\(+\)面の数(\(S\))\(=2\)」が成り立つ。
これは、「『多面体』はすべて『球面』と同じ(位相同型)」であることを示しています。そのほかの曲面、たとえば一番簡単そうな「円板 (中身のある円)」のオイラー標数を計算してみると、これは位相的には「中身のある三角形」と同じですから、
\(\chi(K)=V-E+S=3-3+1=1\)
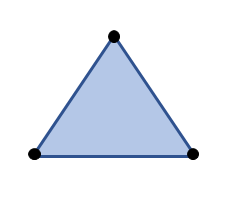
円板のオイラー標数は「\(1\)」で、球面のオイラー標数「\(2\)」とは違う値になります。
また、穴のあいた円板(位相的には円筒と同じ)では、
\(\chi(K)=V-E+S=8-12+4=0\)
と、また違った値になります。
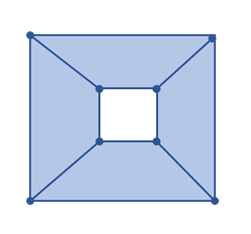
同じ位相多様体のオイラー標数は同じになる、つまりオイラー標数は「位相不変量」であるため、オイラー標数が違えば、位相多様体としては違うものです(しかし、「オイラー標数が同じでも、位相多様体としては異なる」可能性もあります)。
2次元多様体の分類
2次元多様体、すなわち「曲面」については、オイラー標数と境界の数、向き付け可能性ですべて分類ができて、次のようになります。(面倒なので、2つ以上の部分からなるもの(連結でないもの)や、果てがないもの(コンパクトでないもの)は除きました。)
<向き付け可能なもの>
| オイラー標数 | \(2\) | \(1\) | \(0\) | \(-1\) | \(2-2g (g\geq 2)\) |
|---|---|---|---|---|---|
| 境界なし | 球面(\(S^2\)) | トーラス(\(T^2\)) (円環面、浮き輪 |
\(\sum_g\) (\(g\)人乗り浮き輪) |
||
| 境界が1つ | 円盤(\(D^2\)) (穴あき球面) |
穴あきトーラス | |||
| 境界が2つ | 穴あき円板 (アニュラス、円筒) |
<向き付け不可能なもの>
| オイラー標数 | \(2\) | \(1\) | \(0\) | \(-1\) | \(2-2g (g\geq 2)\) |
|---|---|---|---|---|---|
| 境界なし | 実射影平面(\(P^2\)) | クラインの壺(\(K\)) | \(P^2\#\cdots \# P^2\) (\(g\)個の連結和) |
||
| 境界が1つ | メビウスの帯(\(M\)) | 穴のあいたクラインの壺 |
(実は、穴のあいた実射影平面はメビウスの帯と同じです。)
ベッチ数からホモロジー類へ
しかし、2次元多様体の分類では最強の不変量だったオイラー標数も、3次元多様体の分類には全く役に立ちません。なぜなら、3次元閉多様体では、「オイラー標数がすべて0」になってしまうからです!
ここで困ったポアンカレは、新しい概念を構築します。当時は集合論もきちんと整備されておらず、圏論もなかった。そんな中で、ポアンカレは、まずオイラー標数のもととなっている「ベッチ数」に注目しました。「ベッチ数」とは、例えば、境界のない曲面に対する1次元ベッチ数は、「曲面上の閉曲線で、その線に沿って切り開いても曲面が2つに分かれないようなものが(本質的に)何本あるか」を表わします。
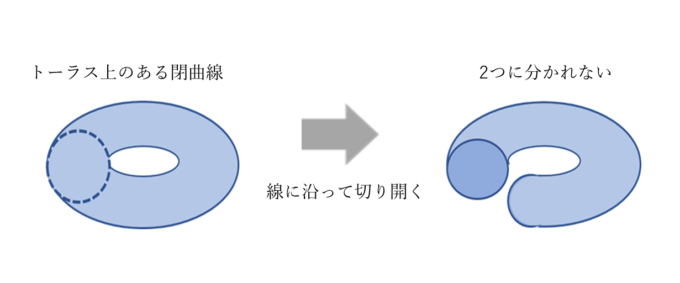
これを一般化すると、境界のない3次元多様体に対する2次元ベッチ数の意味は「3次元多様体上の境界のない曲面(閉曲面)で、その面に沿って切り開いても、多様体が2つに分かれないような面の数」となります。(そもそも「果てはあるが境界のない3次元多様体」をイメージするのが難しいと思いますが……。)
しかしベッチ数だけではうまく行かず(ヒ―ガードによって反例が示されました)、ポアンカレはこの「ベッチ数」にさらに「ねじれ係数」を合わせ、「ホモロジー類」という新しい「位相不変量」を考え出したのです。これが代数的にきちんと整備されて、現代の「ホモロジー群」、「コホモロジー群」へと発展していきます。
基本群で3次元多様体は分類できるか?
今度こそ、この「ホモロジー類」で3次元多様体を分類できると考えたポアンカレでしたが、それもまたうまく行かなかったのです。(ポアンカレは自分で反例を見つけました。)
そこで登場するのが「基本群」です。
3度目の正直で、この「基本群」を使えば3次元多様体を分類できるのでは? とポアンカレは考えました。少なくとも、3次元球面(3次元球体2つをその表面である2次元球面で貼り合わせたもの)であるかどうかくらいは、「基本群」を見ればわかるのではないか? と。これが有名なポアンカレ予想です。
3次元閉多様体で基本群が3次元球面と同じものは、3次元球面(と位相同型なもの)しかない!
数々のトポロジストがこの予想の前に敗れ去って行きましたが、ついに、100年後、ロシアのペレルマンがハミルトンの方法を発展させて、これを証明したわけです。(ここで面白いのは、次元を4以上にした一般化ポアンカレ予想のほうが先に解かれたことです)
ということは、3次元多様体の分類においては「基本群」最強! ということになりそうですね。というわけで、「ポアンカレ予想のはじまり~基本群を学ぼう~」というセミナーを企画いたしましたので、ぜひご参加ください。