電磁気学と特殊相対性理論との深いつながり
公開日
2020年10月23日
更新日
2020年10月23日
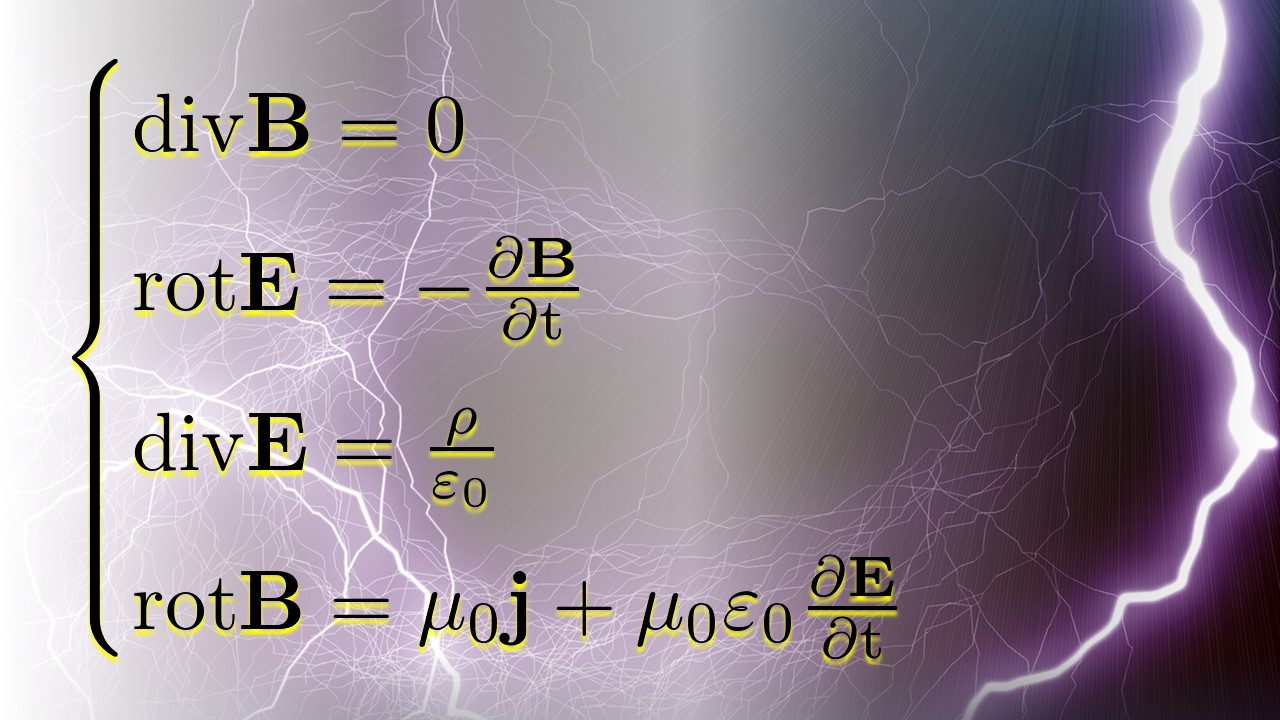
※本記事はロマ数トレラン「マクスウェル方程式から電磁気学を学ぶ」の講師である石山浩一先生による電磁気学と特殊相対論の入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。
この記事の主な内容
古典力学の歴史概観
物理学(科学)の近代化は16世紀のガリレオによっておこなわれました。実験によって、力学的現象が数学的に表現されることを発見したのです。それまではなんと、2000年間もの長い間、ギリシャの哲学者アリストテレスの影響が強く、自然法則は人間の思惟のみから理解できると信じられており、実験や観測によって自然現象を解明することは、ほとんどありませんでした。
天文学者ケプラーが惑星の運動の観測データを解析することにより、コペルニクスの地動説を支持し、ケプラーの法則を発見したことは有名です。ガリレオはケプラーの影響を受けて、自ら発明した望遠鏡を使って地球が動いていることを観測によって確信しました。ガリレオがキリスト司教から迫害を受けたものの、「それでも地球は動いている」という言葉を残したことは有名です。ガリレオは重力による落下運動や振り子の運動を実験により、法則を数学的に表現しました。ニュートンの運動法則の第一法則である「慣性の法則」はガリレオが発見しました。なお、ガリレオは「自然という書物は、数学という言葉で書かれている」と述べています。 (参考までにアインシュタインはこう述べています。「数学は、経験とは無関係な思考の産物なのに、なぜ物理的実在の対象物にこれほどうまく適合するのか?」)
その後、17世紀、ニュートン自ら発明した微積分を用いて、天体運動が万有引力という力によって説明できることを数学的に証明しました。そしてあらゆる力学的な運動がニュートンの運動法則の第二法則である運動方程式(微分方程式)によって記述され、運動方程式を解くことで運動を説明、予測することができるようになりました。20世紀の初頭に原子の世界を記述する量子力学が生まれるまで、力学的基礎理論はニュートンによって完成されたと思われていましたが、原子レベルの世界ではニュートンの力学がもはや通用しないことが明らかになったのです。しかし、現代においてもニュートンの力学は様々な分野で利用されており、現在でも有用であることは疑いありません。量子力学以前の力学を「ニュートン力学」あるいは「古典力学」と呼んでいます。
電磁気学の歴史概観
電磁気現象は古代ギリシャ時代から琥珀の摩擦による静電気により知られていましたが、目に見えず扱いが困難なため、電磁気学の近代科学化は古典力学よりも約200年遅れることになりました。ちなみに、電気を英語でelectricityと言いますが、これは琥珀のギリシャ語の「エレクトロン」が語源です。
18世紀のクーロンの法則の発見、19世紀のエルステッド、アンペールの法則、ファラデーの電磁誘導の発見と続き、電気と磁気が互いに関係することを発見しました。電磁気学の歴史において特に重要な人物はファラデーとマクスウェルです。ファラデーは電場や磁場という「場」の考え方を初めて導入しました。ファラデーは数学的な素養が乏しかったのですが、マクスウェルによって、電磁気の「場」の定式化がなされ、様々な電磁気現象が最終的にわずか4つの方程式(マクスウェル方程式)で表現されたのです。
(注)ファラデーの「場」の概念とマクスウェルの数学の力によって、電磁気学は一気に理論的に発展し、現代物理学の基礎となっていきます。
(注)現在のマクスウェル方程式の形にまとめたのは、実際はヘビサイドとヘルツです。
\[
\begin{cases}
&\rm{div} \boldsymbol{B} =0\\
&\rm{rot} \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}\\
&\rm{div} \boldsymbol{E} =\frac{\rho}{\varepsilon_0}\\
&\rm{rot} \boldsymbol{B}=\mu_0\boldsymbol{j}+\mu_0\varepsilon_0\frac{\partial \boldsymbol{E}}{\partial t}
\end{cases}
\]
「場」の理論について
ニュートンの万有引力とクーロンの法則はどちらも逆二乗の形で非常に似ています。
- 万有引力 : \(\displaystyle F=G\frac{Mm}{r^2}\) (\(G\)は定数)(1.1)
- クーロンの法則: \(\displaystyle F=k\frac{Qq}{r^2}\) (\(k\)は定数)(1.2)
どちらも遠隔作用論と呼ばれ、離れた物体に瞬時に力が働くとする考え方です。ここで、ファラデーによる「場」を用いたクーロンの法則の表現は以下のように表されます。
クーロンの法則:\(F=qE(r)\) (1.3)
クーロンの法則において\(E(r)\)は\(E(r)=k\frac{Q}{r^2}\)で定義される電場です。(1.2)と(1.3)は数学的には単なる置き換えですが、物理的な意味は大きく異なります。「場」というのは近接作用論と呼ばれ、近接した空間を通して力学的な作用が伝搬していく考え方で、考え方に大きな違いがあります。(1.3)は電荷\(Q\)が周囲の空間に電場を作り、その電場が電荷\(q\)に影響を及ぼすのです。マクスウェル方程式は「場」の方程式で、「場」の概念なしには電磁気法則を数学的に統合できません。
それでは、万有引力の法則が「場」の方程式で表されていないのは何故か?すなわち、近接作用論を採用しない理由とは何か?と思われるかもしれません。実はニュートン以前は力の遠隔作用は魔術的なものとして受け入れられていませんでした。また、ニュートン自身、万有引力が遠隔作用であることに納得していなかったのですが、当時の近接作用論は触れ合うもの同士に力が働くという意味の近接作用論で、「場」という概念がなく、また、万有引力の原因が何か本質的に解明できなかったため、万有引力を遠隔作用として位置づけるしかなかったのです。
それでも、ニュートンの力学理論は数学的な成功を収めたため、ニュートン以降の物理学者は力の遠隔作用を受け入れるようになっていたのです。そのため、ニュートンの後に生まれたクーロンもまた、電気力が遠隔作用であることは自然に受け入れたのだと思います。しかし、ファラデーによる「場」という概念によって、力が新しい次元の近接作用論に昇華され、回帰してきたわけです。ここに、ファラデーの物理学への最高の貢献があるのです。そして、アインシュタインが重力の「場」の理論の構築に成功したことで、一般相対性理論が生まれ、重力(万有引力)の原因が質量、すなわち、エネルギーによる時空の歪みであることが解明されたのです。ただし、重力の「場」の理論は、当時の物理学者が知らなかった時空の場を表現する高度な数学(リーマン幾何学)と天才的な物理学的発想が必要でした。このように、物理学の歴史を振り返っても、必要な学問の土壌と適切な人材の出現が適切な時代に生み出されて物理学が発展してきたことに、必然性を感じざるを得ません。
なお、現代物理学では現在発見されている全ての力(重力、電磁気力、強い力、弱い力)は「場」の理論で表現されています。また、その後の物理学の大革命である量子力学の登場によって、量子力学は「場」に量子力学の原理を適用した「場の量子論」へと発展し、今では現代物理学の多くの理論は「場の量子論」の言葉で記述されているのです。
古典力学と電磁気学は矛盾する?
さて、実は古典力学と電磁気学には根本的に矛盾がある、と言ったら驚かれる方も多いかもしれません。古典力学と電磁気学を別々に学ばれることが多いので無理もありません。また、物理学者ですら、マクスウェル方程式が出てくるまでは何の疑問も持たなかったのです。
マクスウェル方程式によって、電磁波の存在が理論的に予言され、ヘルツによって実験で実在が確認されました。さらに、電磁波が光であることも解明されました。光が電磁波ならば光は波動ということになるので、波動を伝える媒質があることになります。それを物理学者は「エーテル」と名付けました。「エーテル」についてはマイケルソン-モーリーの実験と関連して特殊相対性理論の入門書にも出てくるのでご存じの方も多いかもしれません。結局、実験によって、「エーテル」の存在は確認できませんでした。しかし、実験によって「エーテル」の存在が否定されたことよりも、深刻だったのは、古典力学と電磁気学の矛盾だったのです。
この重大性に気づいて、根本的に問題解決したのがアインシュタインでした。特殊相対性理論の原論文名は「動いている物体の電気力学」という名前ですから、アインシュタインが論文で述べたかったことは力学と電磁気学が深く関係していることは明らかです。原論文のまえがきには「エーテル」の存在は不要であると明言しています。論文は第一部の運動学の部と第二部の電気力学の部に分かれており、第二部でマクスウェル方程式が出てきます。第二部によって、電場と磁場の興味深い本質的関係が解明されることになります。いずれにせよ、マクスウェル方程式が特殊相対性理論の起点となっていることは間違いありません。なお、奇しくもアインシュタインはマクスウェルが亡くなった年に生まれています。
では、古典力学と電磁気学の矛盾について説明しましょう。
古典力学の大前提となるのは実はニュートンの運動方程式ではなく、ガリレオが築いた次の2つの原理です。ニュートンはその原理を力学の基礎としたのです。
- (1)ガリレオの相対性原理
- (2)ガリレオ変換
お互いに等速運動している観測者を考えます。一方の観測者がいる座標系を\(S\)とし、\(S\)に対して速度\(V\)で動いている観測者がいる座標系を\(S^{\prime}\)とします。ニュートンの第一の運動法則である「慣性の法則」が成り立つ系を慣性系と呼びます。互いに等速運動している系は慣性系となるので、\(S\)、\(S^{\prime}\)とも慣性系です。このとき、(1)のガリレオの相対性原理は\(S\)、\(S^{\prime}\)ともに物理法則は同じであるというものです。つまり、\(S\)でニュートンの第二法則が成立するのならば、\(S^{\prime}\)系においても同じ法則が成立せねばならないということです。
次に(2)のガリレオ変換について説明します。\(S\)と\(S^{\prime}\)の座標系として、\(x\)方向のみの一次元運動を考えれば系の座標は\((x,t)\)、\((x^{\prime},t^{\prime})\)で表現されます。\(t\)は時間を表します。このとき、座標の変換式は以下のようになります。
- \(x^{\prime}=x-Vt\) (2.1)
- \(t^{\prime}=t\) (2.2)
この\(S\)-\(S^{\prime}\)間の座標変換式(2.1)と(2.2)をガリレオ変換と言います。
(2.1)を\(t\)で微分すると、(2.2)を考慮して
\(v^{\prime}=v-V\) (2.3)
が得られます。これが古典力学における速度の合成則です。
ここで、(2.3)を\(v=v^{\prime}+V\)と変形すると、\(S^{\prime}\)系において、速度\(v^{\prime}\)で運動している物体は\(S\)系では\(v^{\prime}+V\)の速度で運動しているように見えるということを表しています。
さらに(2.3)を\(t\)で微分すると加速度の関係式が得られます。加速度を\(a\)とすると、\(V\)は定数ですから、
\(a^{\prime}=a\) (2.4)
となります。ニュートンの運動法則の第二法則である運動方程式は\(ma=f\)(\(m\)は質量、\(f\)は力)ですから、
\(S\)系の運動方程式は以下のように表されます。
\(S\)系:\(ma=f\) (2.5)
次に、\(S\)系の運動方程式(2.5)を\(S^{\prime}\)系での運動方程式に変換すると、(2.4)を用いて
\(a\)→\(a^{\prime}\)に変換すれば良いので、\(S^{\prime}\)系の運動方程式は、
\(S^{\prime}\)系:\(ma^{\prime}=f\) (2.6)
となり、いずれの系においてもニュートンの第二法則が成立ちます。
このように、ガリレオの相対性原理はガリレオ変換において物理法則が不変であることを要請します。
それでは、電磁気学についてはどうでしょうか?光の速度は運動していようといまいと光速度不変であることがマイケルソン-モーリーの実験で確認されていますから、(1.3)の速度の合成則が成立せず、ガリレオ変換が成立ちません。もし、ガリレオ変換が成立つとすれば、\(S\)系で成立っていた電磁気学の法則が\(S^{\prime}\)系では成立たなくなり、ガリレオの相対性原理が成立ちません。このことを確かめるためにはマクスウェル方程式にガリレオ変換をおこなってみると明らかです。
このようにガリレオ変換を用いると、ある慣性系では、例えば電磁誘導の法則が成立つのに、別の慣性系では成立たなくなる、ということになり、もはや物理法則として認めるわけにはいきません。慣性系同士においては全ての物理法則が不変と考えるのが自然です。これこそが、アインシュタインの相対性理論の大きな柱である、アインシュタインの相対性原理です。結論から言うと、マクスウェル方程式はガリレオ変換ではなく、ローレンツ変換において不変となります。このように、古典力学と電磁気学は相容れない根本的な大きな矛盾があるのです。
\[
\begin{cases}
&x^{\prime}=\frac{x-vt}{\sqrt{1-(v/c)^2}}\\
&t^{\prime}=\frac{t-(v/c^2)x}{\sqrt{1-(v/c)^2}}
\end{cases}\]
特殊相対性理論
古典力学と電磁気学の矛盾について説明しました。もう、おわかりだと思いますが、アインシュタインはガリレオの相対性原理を捨てて、電磁気学の原理を採用し、ニュートン力学を修正したのです。ローレンツ変換は既にローレンツが導いていますが、その導出は「エーテル」の存在と実験結果を合わせるための単なる数学的な操作に過ぎませんでした。しかし、アインシュタインの発想は全く独創的なものでした。古典力学は時間において、(2.2)を採用しています。日常感覚では何の疑問も持たずに時間は不変という前提で考えていますが、アインシュタインは本当に、時間は絶対的不変なのか?ということを改めて考え直すために、同時刻とは何か?という問いを思考実験で突き詰めていきました。こうして、アインシュタインはローレンツとは全く異なる独創的なアプローチでローレンツ変換を導いたのです。ここにアインシュタインの常識に捕らわれない類い希なる洞察力を垣間見ることができます。
アインシュタインがおこなったことは、古典力学にもローレンツ変換が適用できるように修正したことなのですが、これが結果的に特殊相対性理論において最も有名な「時間は運動によってリズムを変える」という常識を越えた新しいパラダイムを生むことになるのです。あまりに奇抜で最初は誰も信じなかったのですが、後に実験で正しいことが検証され、アインシュタインの名前は世界中に広がったのです。そして、特殊相対性理論はSFの世界に取り込まれ、今でも多くのSFファンを魅了しています。(私もまた、その世界に憧れて物理学を目指したSFファンの一人なのですが。)今では物理を学んだことがない人でさえ、アインシュタインや相対性理論という名前だけは知っているようです。しかし、物理学の歴史上で重要なことは、むしろ特殊相対性理論によって古典力学、電磁気学に初めて同一原理が適用できるようになったことなのです。
対応原理
新しい理論は必ず古い理論を内包していなければなりません。これを「対応原理」と呼んでいます。ニュートン力学は近似的には正しいので、特殊相対性理論はニュートン力学を含んでいなければなりません。特殊相対性理論はニュートン力学を修正しましたが、慣性系同士の速度が光速に比べて小さいと見なすことができるとき、これまでの古典力学と完全に一致するのです。つまり、特殊相対性理論は「対応原理」を満たしています。一般相対性理論もまた、重力が弱いとき、ニュートンの重力理論と完全に一致し、「対応原理」を満たしています。
(注)ボーアの対応原理が有名ですが、ボーアの対応原理は古典力学と量子力学との関係に限定したものです。
一般相対性理論とその先
特殊相対性理論は慣性系のみにおいて成立ちますが、系に加速度が生じている場合(非慣性系と呼びます)には適用でいないことが、アインシュタインは不満だったのでした。そのために、次のステップとして、一般相対性理論の構築を目指したのです。そして特殊相対性理論の発表から約10年後、一般相対性理論が完成しました。そしてこの時、初めて古典力学と電磁気学が完全に融合したのです。電磁気学が「場」の理論、すなわち近接作用論で表現されているため、古典力学も「場」の理論で表現されなければなりません。前に述べたように、一般相対性理論は「場」の理論ですから、この時、古典力学と電磁気学が近接作用論で融合されたのです。そのため、一般相対性理論と電磁気学を総称して「古典場」の理論と呼んでいます。(「古典場」と対応するのが「量子場」です)
このような流れから考えれば、融合をさらに進めて、力学と電磁気学を完全に同一方程式で統合したいと考えるのは自然でしょう。アインシュタインは晩年、上記の統一理論である「統一場理論」に没頭することになりますが、残念ながら達成することはありませんでした。しかし、アインシュタインの夢は現代の物理学者に引き継がれています。現在の多くの物理学者は「全ての力」の統一理論を探し求めて日々健闘しているのです。その統一理論の有力候補が「超弦理論」や「ループ量子重力理論」なのです。ただし、現時点では未だアインシュタインの夢は実現されていません。
理論物理学の魅力
電磁気学は古典物理において、力学とは異なり、目に見えない現象を扱うことで抽象的な概念が沢山出てきます。おまけに多くの現象や法則(方程式)を各論的に学ぶために、電磁気学はニュートン力学の運動方程式のような統一感がなく、雑多でわかりにくいと感じた方も多いかもしれません。電磁気学は工学のための基礎理論に過ぎないと思っている方も多いでしょう。
しかし、実際は電磁気学こそ、現代物理学のエッセンスが詰まっているだけでなく、理論物理学の魅力と美しさを学ぶのに最適な教材なのです。既に述べたように、電磁気法則は「場の理論」を通してマクスウェル方程式に統一され、その方程式は電磁波(電波)の存在を予言しました。私達の現在の便利な暮らしがあるのは電磁波のおかげです。マクスウェル方程式が電磁波を予言したように、優れた物理方程式には未発見の現象や存在を予言する力があります。アインシュタインの一般相対性理論の方程式もまた、重力波やブラックホールを予言し、実験や観測で実証されました。また、ディラックは量子力学と特殊相対性理論を融合することで、ディラック方程式を発見し、その方程式は陽電子を予言しました。最近では素粒子物理学の標準理論ではヒッグス粒子が予言され、実験で存在が検証されました。このような例は現在では、枚挙に暇がありません。
このように、数学で表現された物理理論から導かれる方程式が未発見の現象や存在を予言し、それが実験で立証される、そこに理論物理学の魅力と自然の不可思議があります。ここで、アインシュタインの言葉「数学は、経験とは無関係な思考の産物なのに、なぜ物理的実在の対象物にこれほどうまく適合するのか?」が強く蘇ってきます。数学も物理も論理的な科学であるにもかかわらず、その理論が理論的かつ数学的に導かれ、実験で正しいことがわかったとしても、何故、その理論が正しいのか、何故、自然はその理論を採用しているのか、不思議でならないという思いに駆られることも少なくありません。
マクスウェル方程式と相対性理論への誘い
さて、これまで述べてきたように、マクスウェル方程式と特殊相対性理論には理論物理学の魅力が満載です。そして、その魅力を少しでも感じてみたいと思われるのでしたら、マクスウェル方程式を学んだ後、アインシュタインの原論文を読むことをお勧めします。
特殊相対性理論の論文は科学論文としてお手本中のお手本と言われています。論理の展開は極めて明快で、第一級の論文と言われています。それでいて、使用される数学は大学1~2年生レベルで決して高度なものではありません。文庫本(岩波文庫)のわずか60ページに原論文が収められています。
以上を通して伝えたいことは、マクスウェル方程式を理解することを通して特殊相対性理論を深く理解することができるということです。そして、アインシュタインの素晴らしい天才的思考を辿るには入門書や教科書ではなく、原論文を読まなければなりません。論文の中で、アインシュタインは電磁気学の問題点として電磁誘導とローレンツ力の問題を最初に提起しています。本質的には運動の相対性が関わっているからです。論文の第二部において、上記の問題が議論されます。そもそも、マクスウェル方程式にはローレンツ力が含まれていないので、マクスウェル方程式からローレンツ力は導かれません。ローレンツ力と他の力とは何が違うのか?このこと踏まえて論文を読んでみると興味深いものがあります。
アインシュタインの論文を読み、特殊相対性理論を学ぶことで、電磁気学をさらに深く学ぶこともできます。電磁気学と特殊相対性理論に関わる話は尽きませんので、ローレンツ力の問題、電場と磁場の関係等、これらの説明は次の機会に譲ることとします。
<文/石山浩一>