数学教室和(なごみ)講師の松中です。

先日こちらの記事で複素関数の世界を紹介させていただきました。

美しき複素関数の世界

この記事の要約は

• ・日常生活で私たちが使っている数は実数と呼ばれる数である。
• ・複素数とは実数を含む数の体系である。
• ・複素数を入れる関数である複素関数は美しい。

　
となります。

記事の中で、$\sin{x}$の$x$に入れる数を実数の世界から複素数の世界まで拡張すると$\sin{x}$は$2$にも$100$にもなれるということを紹介しました。

つまり$\sin{x}=2$は複素数の世界では解をもつのです！

先日も和(なごみ)のオンライン打ち合わせの後に、キラキラ数学プロジェクトの一環として社内スタッフにこの話を紹介しました。

本記事では$x$にどんな数を入れると$\sin{x}$が$2$になるのかを実際に求めてみようと思います。上の動画でもほぼ同じ内容を話していますので、聴覚優位な方は動画をご参照ください。

そもそも複素数の世界の$\sin$とは?

まずは$\sin{x}$の$x$に複素数を入れるため、$\sin{x}$の定義を拡張していきます。

高校の定義では複素数を入れることができない

さて、高校の時$\sin{\theta}$の値は次のように定義しました。

「原点から角度$\theta$の方向に直線をひくとき、その直線と原点を中心とする半径$1$の円の交点の$y$座標が$\sin{\theta}$」

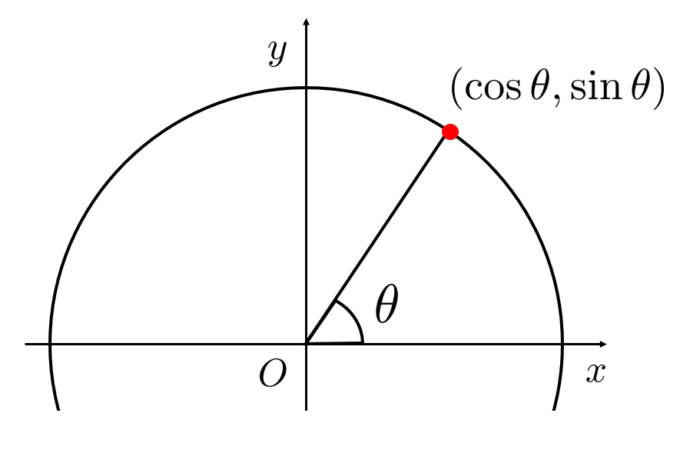
$\sin{\theta}$は単位円週上の$y$座標であるため、図から$\sin{\theta}$の値が$-1$以上$1$以下であることは明らかです。実際$y=\sin{x}$のグラフは次のようになります。

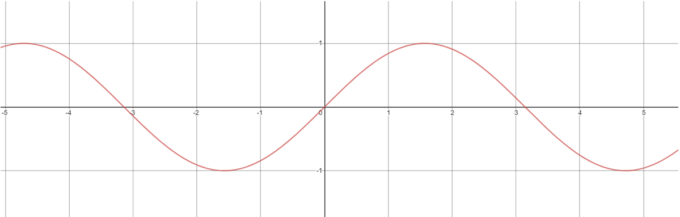
「さあ、では$\theta$に複素数を入れてみよう！」となるのですが、角度$i$とはどんな角度かさっぱりわかりません。つまりこの定義では$\sin{i}$の値すら求めることができないのです。

世界の拡張

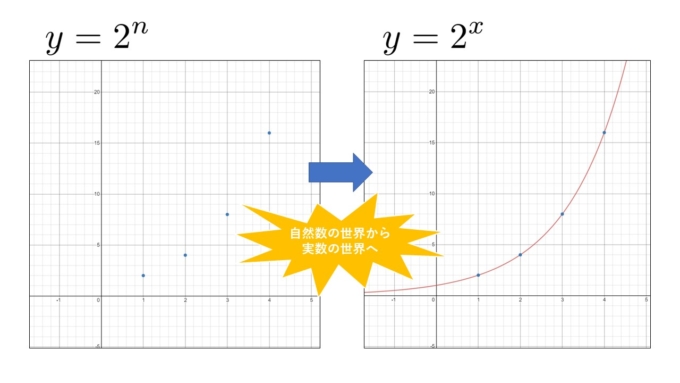
数学の世界では往々にしてよく知られた概念をより広い世界に拡張していきます。例えば自然数で定義された$y=2^n$という指数関数から、実数で定義された$y=2^x$への拡張などです。

世界を拡張するとき、好き勝手に拡張してしまってはこれまでの理論と整合性が取れなかったり、美しくなかったり意味がない拡張となってしまいます。そのため、数学者達は拡張前の世界でよく知られている性質や定理が、拡張された世界でも成り立つことを要請しながら定義を拡張していきます。例えば先の$y=2^n$の関数の拡張は指数法則を拠り所にしています。$y=2^x$という実数の世界の指数関数でも指数法則が成り立つように慎重に定義を拡張していったのです。

では$\sin{x}$は$\sin$のどのような性質を拠り所にして定義を拡張するのでしょうか。高校で学んだ直角三角形や単位円での$\sin$の定義、加法定理などの性質では簡単に複素数の世界に拡張できそうもありません。

$\sin{x}$を複素数の世界に拡張するときの拠り所となるもの、それは「$\sin{x}$のテイラー展開」です。高校ではテイラー展開は習いませんが、数Ⅲの問題ではよく、

$$\sin{x}>x-\frac{x^3}{6}$$

のような謎の不等式が出てきていました。大学で微積を学ぶとこれは$\sin{x}$のテイラー展開の一部であったことが分かります。$\sin{x}$のテイラー展開とは具体的には以下の式です。
$$\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$

右辺は中学、高校で習った多項式を無限次にしたようなものであり、テイラー展開を使えば単位円を書かなくても、右辺の計算を続けていくことで$\sin{x}$の値を求めることができます。

例えば$\displaystyle \sin{\frac{\pi}{6}}=\frac{1}{2}$ですが、

$$\frac{\pi}{6}-\frac{1}{3!}\left(\frac{\pi}{6}\right)^3+\frac{1}{5!}\left(\frac{\pi}{6}\right)^5$$
を計算すると、答えは$0.50000213\cdots$になります。上の計算では途中で足し算を打ち切ってしまっているため、正確に$\displaystyle \frac{1}{2}$にはなりませんでしたが、この先ずっと計算を続けていくことでいくらでも$\displaystyle \frac{1}{2}$に近づきます。

単位円上の$y$座標として定義された$\sin{\theta}$の値が、このような比較的単純な計算を続けていくことで計算できることは何とも不思議です。

$\sin{x}$を複素数の世界に拡張するときは、このテイラー展開を拠り所にします。もっと言うとこのテイラー展開自身を$\sin{x}$の定義とするのです！

ここで、普通$y=f(x)$と書くと実数の関数を意味するため、複素関数の慣習である$w=f(z)$の表記でテイラー展開の式を書き直しておきます。変数を$x$から$z$に書き換えた以下の式こそが複素数の世界における$\sin{z}$の定義となります。
$$\sin{z}=z-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\cdots$$

$\sin{z}$に複素数の値を入れてみよう

さて$\sin$に複素数を入れることができるようになったので、実際に複素数を入れて値を見てみましょう！まずは先ほど求めることができなかった$\sin{i}$の値を求めましょう。

$$\sin{i}=i-\frac{i^3}{3!}+\frac{i^5}{5!}-\frac{i^7}{7!}+\cdots=i\left(1+\frac{1}{3!}+\frac{1}{5!}+\frac{1}{7!}+\cdots\right)$$

、、、この値が何になるか全くわかりませんね。。。このように$\sin$の定義をそのまま拡張しただけでは簡単にその値を求めることができません。

指数関数登場

そこで活躍するのが高校で学ぶ指数関数$y=e^x$です。$e$はネイピア数と呼ばれるとても大事な実数の定数で、およそ$2.71828$となります。

この指数関数もテイラー展開可能で以下のようになります。

$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots$$

指数関数$y=e^x$もテイラー展開を拠り所にして複素数の関数として定義し直します。複素数$z$に対して指数関数$w=e^z$を

$$e^z=1+z+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\cdots$$

として定義します。

$\theta$を実数として$z$に$i\theta$を代入してみます。
すると
$$\begin{align*} e^{i\theta}&=1+i\theta+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}+\cdots\\\\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\cdots\right)+i\left(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots\right)\\\\ &=\cos{\theta}+i\sin{\theta} \end{align*}$$

となります。ここで先ほどの$\sin{\theta}$のテイラー展開と、以下の$\cos{\theta}$のテイラー展開を用いています。
$$\cos{\theta}=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\cdots$$
結局分かったことは指数関数$w=e^z$の$z$に$iθ$を代入すると、
$$e^{i\theta}=\cos{\theta}+i\sin{\theta}$$
となることです。この式の嬉しいところは、$\theta$が実数であるため、右辺の$\cos{\theta}$、$\sin{\theta}$は私たちが良く知っている三角関数となり、高校数学の知識だけで計算することが可能なところです。

例えば$\displaystyle z=\frac{\pi}{6}i$として、
$$e^{\frac{\pi}{6}i}=\cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}}=\frac{\sqrt{3}}{2}+\frac{1}{2}i$$
と簡単に値を求めることができるのです。

$\sin{z}$の別表示

ではこの指数関数$e^z$を用いて、$\sin{i}$のような具体的な値を計算できる$\sin{z}$の表示式を求めてみます。

$$e^{i\theta}=\cos{\theta}+i\sin{\theta}$$
は任意の$\theta$で成り立つので、$\theta$を$-\theta$にすると、$\cos{(-\theta)}=\cos{\theta}$、$\sin{(-\theta)}=\sin{\theta}$より、
$$e^{-i\theta}=\cos{\theta}-i\sin{\theta}$$

となります。この2つの式の辺々を引くことで
$$e^{i\theta}-e^{-i\theta}=2i\sin{\theta}$$
となり、これから
$$\sin{\theta}=\frac{e^{i\theta}-e^{-i\theta}}{2i}$$
として$\sin{\theta}$を書き直すことができます。

$\theta$は実数として議論を進めてきましたが、一般の複素数$z$を用いて
$$\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}$$
として複素関数$\sin{z}$を定義し直しても、$e^z$のテイラー展開を考えることで$\sin{z}$の最初のテイラー展開の定義と一致することが簡単に確認できます。これはテイラー展開とは異なる$\sin{z}$の表示式と言えます。

ついに我々は複素関数$\sin{z}$の値を計算しやすい表示を手に入れることができたのです。テイラー展開の定義では簡単に計算できなかった$\sin{i}$の値ですが、この表示を用いると、
$$\sin{i}=\frac{e^{i^2}-e^{-i^2}}{2i}=\frac{e-\frac{1}{e}}{2}i$$
として値を簡単に値を求めることができます。

$\sin{z}=2$となる$z$を求める

準備が整いました。それでは$\sin{z}=2$となる$z$を求めてみましょう。計算の見通しをよくするため複素数$z$を実数$x$、$y$を用いて$z=x+iy$と表すことにします。

まず、$\sin{z}=2$から
$$\frac{e^{iz}-e^{-iz}}{2i}=2$$
の両辺に$2ie^{iz}$をかけて整理することで
$$(e^{iz})^2-4ie^{iz}-1=0$$
の形に変形できます。これは$e^{iz}$を1つの塊とみるとただの二次方程式であるため、中学校で学んだ解の公式を用いて、
$$e^{iz}=2i\pm\sqrt{3}i=(2\pm\sqrt{3})i$$
となります。
ここで左辺は
$$e^{iz}=e^{i(x+iy)}=e^{-y+ix}=e^{-y}e^{ix}=e^{-y}(\cos{x}+i\sin{x})$$
と表せます。これは$e^{iz}$の極形式とみることができ、絶対値が$e^{-y}$、偏角が$x$であることが見て取れます。なお、$e^z$はテイラー展開を拠り所にして定義したため、指数法則$e^{z_1+z_2}=e^{z_1}\times e^{z_2}$が成り立つことは自明ではありませんが、問題なく成り立つので安心してください。上の式変形ではこの指数法則も使用しています。

また右辺も極形式で表すと、
$$(2\pm\sqrt{3})i=(2\pm\sqrt{3})\left(\cos{\frac{\pi}{2}}+i\sin{\frac{\pi}{2}}\right)$$
となるので、左辺と右辺の絶対値と偏角をそれぞれ比べることで、結局次の連立方程式を解けばよいことが分かります。

$$\left\{\begin{align} e^{-y}&=2\pm\sqrt{3}\\\\ x&=\frac{\pi}{2}+2n\pi \end{align}\right.$$

ここで偏角は$n$を整数として$2n\pi$の任意性があることに注意しましょう。

第1式の$e^{-y}=2\pm\sqrt{3}$はただの実数関数の指数関数のため、高校で学んだ$\log$を使って簡単に解くことができ、$y=-\log(2\pm\sqrt{3})=\pm\log(2+\sqrt{3})$となります。$z=x+iy$でしたから、以上で、$\sin{z}=2$となる$z$を求めることができました！

$$\sin{z}=2 \Rightarrow z=\left(\frac{1}{2}+2n\right)\pi\pm i\log(2+\sqrt{3}) \,\,\,\,\,\,(n\text{は整数})$$

手計算は不安なので、実際にコンピュータで間違いがないか計算してみましょう。例えば$n=1$、虚部の符号は$+$として、$\displaystyle z=\left(\frac{1}{2}+2\right)\pi+i\log(2+\sqrt{3})$を$\sin$の中に入れてます。計算にはwolframというwebの計算ソフトを使いました。

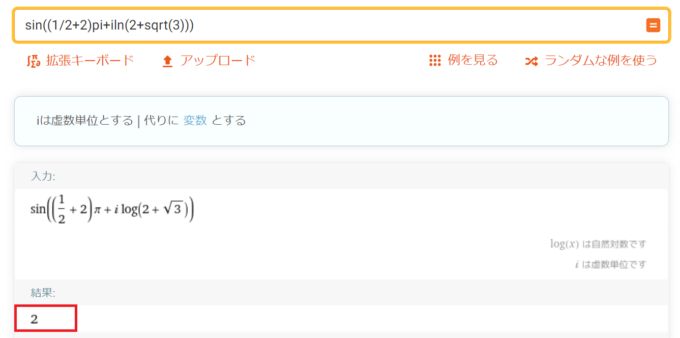
たしかに$2$が出てきていることが分かります！

まとめ

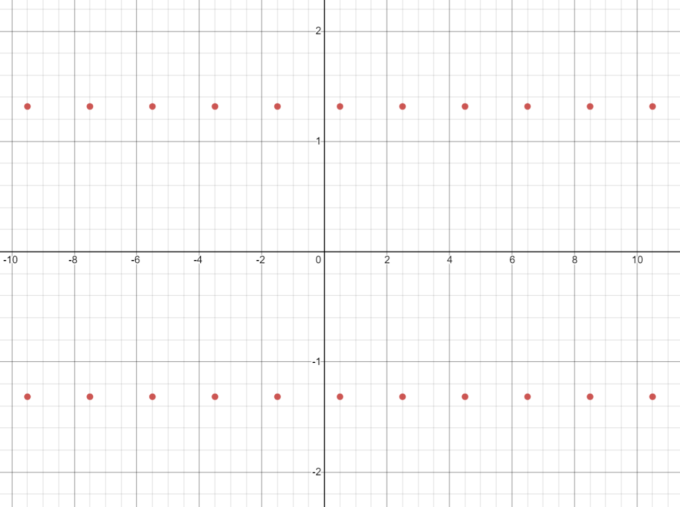
無事$\sin{z}=2$となる$z$を求めることができました。

実数の世界で$\displaystyle \sin{x}=\frac{1}{2}$となる実数が無限個あったことと同様に、$\sin{z}=2$となる複素数も無限個あることが分かります。実際に複素平面上でこれらの$z$をplotすると以下のようになります。行儀よく横に並んでいる様子が面白いです。

テイラー展開は高校では学びませんが、高校数学＋αの知識で複素関数を堪能できることが分かりました。今回紹介したお話は、複素関数の入り口にすぎません。この先には深淵な定理がたくさん待っています。興味を持たれたら是非勉強してみてください！

参考文献)
複素関数の勉強の最初の一冊としておすすめ、神保 道夫先生の「複素関数入門」

<文/松中>