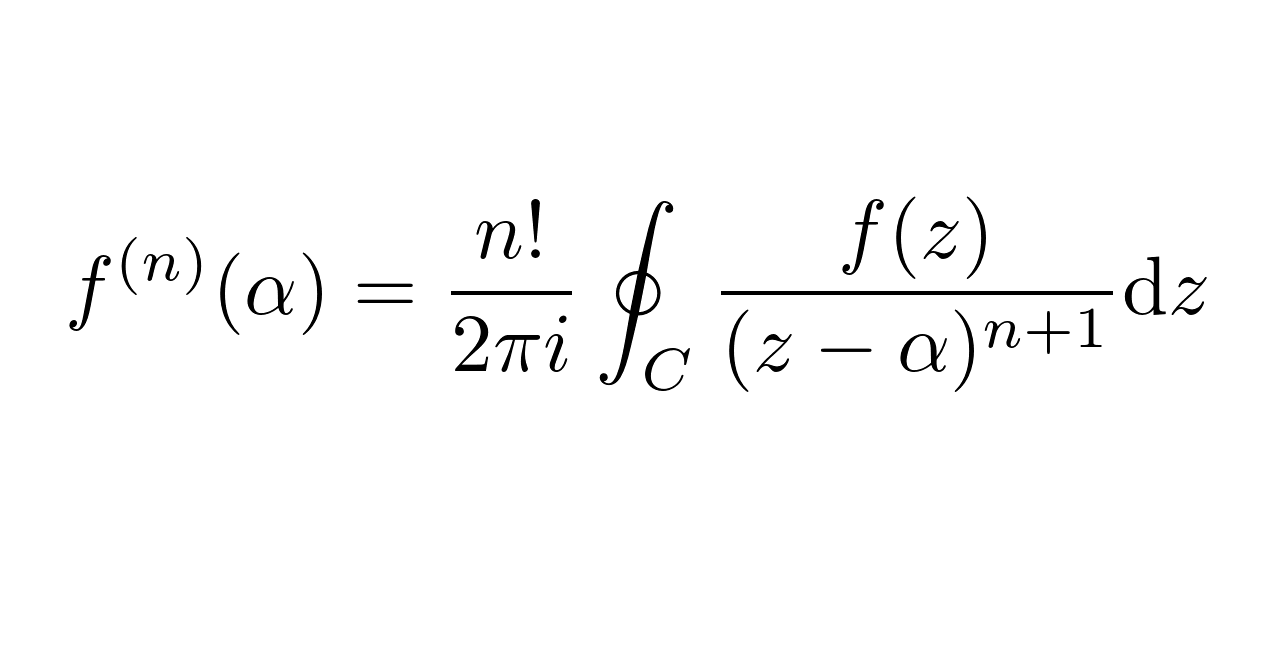
動画で見たい方はこちら↓↓↓

和講師の松中です。

すっかりシリーズ化してきた「和から講師名刺の数式」ですが、今回は私の名刺に書かれている大学時代に一番「すげー！」と衝撃を受けたコーシーの積分公式について触れたいと思います。

コーシーの積分公式は複素解析の分野に登場する数式です。この数式の意味をきちんと理解するためには複素関数の微分、積分の知識が必要となってしまい、残念ながらページの都合上本記事では解説することはできませんが、代わりに今回は複素関数という言葉聞いたことのない方向けに、それがどのようなもので、何がすごいのかについてお伝えしたいと思います。

複素数とは

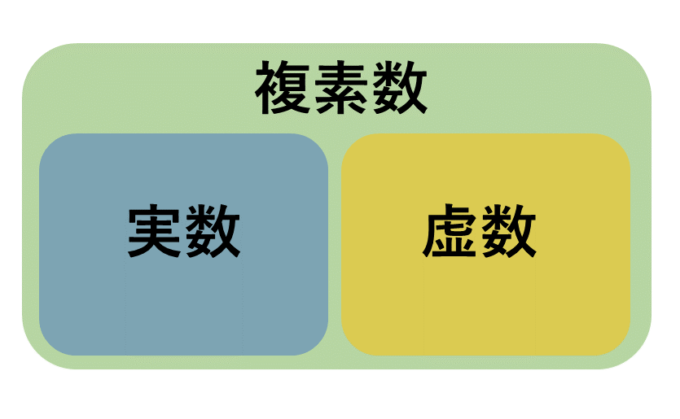
複素関数の「複素」とは複素数を意味するので、まずは複素数について解説します。複素数は高校で習った方も多いと思いますが、ざっくりいえば実数と虚数を合わせた数です。

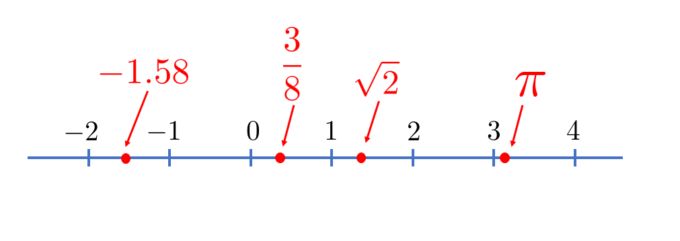
私たちが日常で目にする数はほとんどが実数です。というか全て実数といってよいでしょう。ハンバーガーの料金120円、ドラマ視聴率$23.2$%、半径$3$cmの円周の長さ$6\pi$cm等々これらに出てきている数は全て実数です。実数は小学校から学んでいること、数直線と1対1に対応することから、まさに実在を実感できる数(=実数)としてとてもなじみ深いものです。

一方虚数は$2+3i$、$-1+2i$といった数のことで、よく知っている実数に、よくわからない記号$i$がくっついている数になります。この$i$は実数ではない新しい数であり虚数単位と呼ばれています。$i$は2乗すると$-1$になることで特徴づけられます。

$i^2=-1$

私たちは中学校で「正の数」×「正の数」=「正の数」、「負の数」×「負の数」=「正の数」、$0$×$0$=$0$と習っています。つまり中学校の教科書が正しければ同じ数を二回かけて負の数になるわけがないのですが、どういうわけか$i$を2乗すると負の数になります。

実は中学校の教科書に出てくる「数」は暗黙に実数の事を指しているため、「どんな数も2乗すると$0$以上の数になる」という性質は実数の性質だったわけです。虚数も含めた新しい数の体系である複素数に対しては、過去私たちが学んだ様々な数の性質が成り立つとは限らなくなります。そもそも、複素数には(自然に)大小関係が定義できず、負の数と正の数という概念すらないのです。さあ、$i^2=-1$を受け入れましょう。

虚数なんて存在しない?

と言っても、「2乗すると$-1$になる数なんておかしい、ふざけるな」と思う方もいらっしゃるかもしれません。それは幼少のころから実数に慣れすぎていた弊害です。どんな人もモノの数を数えるために$1$、$2$、$3$、、という自然数を最初に学びます。その後、分数、小数、負の数を学んでいくわけですが、おそらく最初にこれらの数を見たときに「なんだこの数は？」という感情を抱いたはずです。

その実例として私の小学校低学年の時の体験をお話しします。母親が運転する車に乗って窓の外を眺めていると、道路標識に書かれた「$1/7$」、「$2/7$」、「$3/7$」、という分数が次々に私の目に入ってきました。そのうち、「$7/7$」、「$8/7$」となったわけですが、その時に、「7分の3は1を7個に分けた3個分だから、$8/7$という数はおかしい。8個もないから、1を超えることはおかしい」と母親に話した覚えがあります。その当時分数自体は習っていたようですが仮分数の概念はまだ持ち合わせていなかったようです。

ここで言いたいことは、自然数以外の数については、最初にそれを目にしたときに少なからず抵抗があったはず、ということです。しかし日常生活で毎日目にするうちにそれらの数を昔から知っている当然の存在であるという感覚に陥り、2乗すると負の数になるような日常では目にすることのない新しい数に対して「おかしい、ふざけるな」と思ってしまうのです。

以下のようなシチュエーションを想像してみてください、

負の数を知らない人が「$5$を足して$3$になる数？そんな数は存在しない、ふざけるな」と言っている。
分数を知らない人が「$7$倍して$8$になる数？そんな数は存在しない、ふざけるな」と言っている。
無理数を知らない人が「2乗して$2$になる数？そんな数は存在しない、ふざけるな」と言っている。

思わず「$-2$だよ」、「$8/7$だよ」、「$\sqrt{2}$だよ」と教えてあげたくなりますよね。なので今後は「2乗して$-1$になる数？そんな数は存在しない、ふざけるな」と言っている人を見かけたら、優しく「それは$i$だよ」と言ってあげましょう。

私がよくお客様に話すのは「$i$は$1$が存在していると思えるのと同じくらいに存在しており、$i$は$1$が存在していないと思えるのと同じくらいに存在していない。」です。数が本当に存在していているかどうかは(哲学的過ぎて)私にはわかりませんが、$i$だけ特別扱いするのはおかしいということです。

虚数はなぜ生まれた？

「2乗して$-1$になるような数を新しく導入したことは分かったが、そんな見たこともない数をなんで導入するの？」と次の疑問が浮かびます。この質問には前節で説明した内容がそのまま答えになります。

つまり(代数)方程式を解くためです。

「$x+5=3$」を解くために「$x=-2$」という負の数が、「$7x=8$」を解くために「$x=8/7$」という分数が、「$x^2=2$」を解くために「$x=\sqrt{2}$」という無理数が新しく導入されました。
それと同じように、「$x^2=-1$」を解くために「$x=i$」という虚数が新しく導入されたのです。

これはなかなかすごいことで、どの方程式も「そんな$x$は存在しない」と一言で片づけてもよかったはずです。過去の数学者が果敢に方程式と向き合って新しい数を発見してきたのです。新しい数を導入するとき不安でしかなかったのでしょう。そのため新しい数には負の数、無理数、虚数といった、まさにマイナスのイメージの名前が付けられているのです。

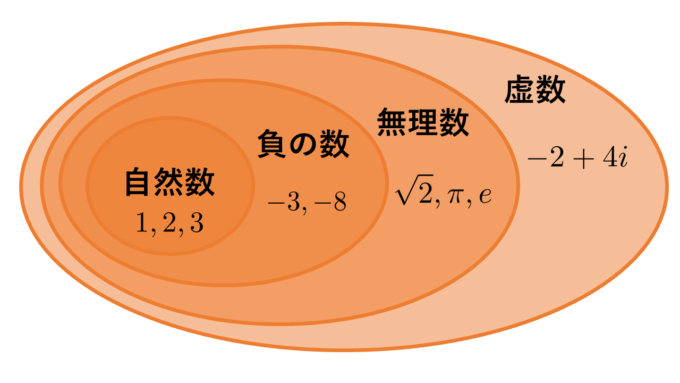
方程式を解くために数の世界を広げてきたわけですが、これ以上広げる必要はないのでしょうか？複雑な方程式を作れば、もっと数の世界を広げないとその方程式を満たす$x$が存在しないような気にもなります。実は複素数まで数の世界を広げると、どんな(代数)方程式も複素数の解をもつことが知られています。これは「代数学の基本定理」と呼ばれるもので、あの大天才ガウスが1799年21歳の時に証明しています。
人類が良く知っている数から方程式を作って、どんどん新しい数を追加していく。その最終形態が複素数なのです！

※もちろん自然数から始めて代数方程式を解くためだけに数を追加していくと、最終形態は複素数ではなく、その部分集合の代数的数の集合$\overline{\mathbb{Q}}$になります。ここでは人類が図らずも$\pi$や$e$などの超越数を認知してしまったため、実数全体を人類が良く知っている数としました。

複素関数の世界へ

高校で学ぶ関数$f(x)$とは実数$x$を入れると実数$f(x)$が出てくるルールの事でした。一方複素関数$f(z)$とは複素数$z$を入れると、複素数$f(z)$が返ってくるルールの事です。$x$でなく、$z$を使うのはただの慣習です。$f(z)$と書かれていたら、この関数は複素関数なんだなと認識でき、わざわざ断る必要がなく便利なのです。
例えば簡単な複素関数として$f(z)=z^2$という関数を紹介します。この関数は中学、高校で習った二次関数$f(x)=x^2$を複素数の世界に拡張した複素関数です。

$f(1)=1^2=1$
$f(2)=2^2=4$
$f(3)=3^2=9$

という風に$z$に実数を入れると当然その2乗が出てくるだけで新鮮味はないのですが、実数でない複素数(虚数)を入れてみると

$f(i)=i^2=-1$
$f(1+i)=(1+i)^2=1^2+2\cdot 1\cdot i + i^2=1+2i-1=2i$
$f(3+4i)=3^2+2\cdot 3 \cdot i +(4i)^2 = 9+6i-16=-7+6i$

となって関数から出てくる値も一般に実数とは限らない複素数となります。とても簡単な関数ですが、複素数を入れると複素数が出てくるため、これは立派な複素関数です。

また、高校で習った$\sin{x}$、$\cos{x}$、$e^x$、$\log{x}$という有名な関数たちもちゃんと複素数でも定義されています。例えば$\sin{x}$を見てみましょう。$\sin{x}$のグラフは以下のように$-1$と$1$の間を振動する波の形になっています。

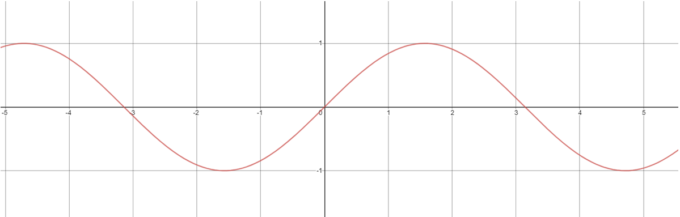
高校生に「$\sin{x}=1/2$となる$x$は?」と質問すると、「$x=30^\circ$」とか、「$x=\pi/6$」と答えるでしょう。しかし「$\sin{x}=2$となる$x$は?」と質問しても、「$\sin{x}$は$-1$以上$1$以下だからそんな$x$は存在しない」と答えるはずです。高校生は$\sin$の中に実数しか入れないので仕方ないのですが、驚くべきことに変数$x$が取り得る範囲を実数から複素数に広げると「$\sin{x}$=2」は解をもつのです!

$\sin{x}$は変数$x$が実数という監獄に入れらているため自由に動くことができず取り得る値が$-1$と$1$の間の実数に縛られていました。しかし変数$x$を実数の監獄から複素数という自由な世界に出してあげることで、$2$になれるばかりか$100$や$10,000$といった好きな値をとることができるのです！

上の図は変数の範囲を複素数に広げた$\sin{z}$のグラフです(実部だけを描画しています)。実数のグラフからは想像できないほど躍動的に値が変化していることがわかりますね。窮屈だった実数の世界から解放されて喜んでいる$\sin{z}$さんを見ると、関数は本来実数の世界に住んでいるわけではなく、複素数の世界に住んでいるということを彷彿とさせます。

そんな考えを抱くのは私だけではありません。以下は、日本の大数学者高木貞二先生が「近世数学史談」の中で訳された、ガウスからベッセルへの手紙の一部です。

　
これはガウスの書いた手紙ですが、高木先生もこの手紙に共感するものがあったから「近世数学史談」で取り上げたのでしょう。過去の大数学者たちが「関数は複素数の範囲で考えるべき、そして、複素関数は美しい」と言っているのです。私の名刺に書いてある「コーシーの積分公式」がすごそうだ、美しそうだ、ということはわかっていただけたのではないでしょうか。

複素関数の世界には「コーシーの積分公式」以外にも美しい定理がたくさんあります。特に「一致の定理」には興奮します！興味を持たれたら是非勉強してみてください。そこにはあなたが今まで知らなかった美しい世界が待っていることでしょう。
<文/松中>

参考文献)
・ガウスからベッセルへの手紙が載っている、高木貞二先生の「近世数学史談」

・複素関数の勉強の最初の一冊としておすすめ、神保 道夫先生の「複素関数入門」