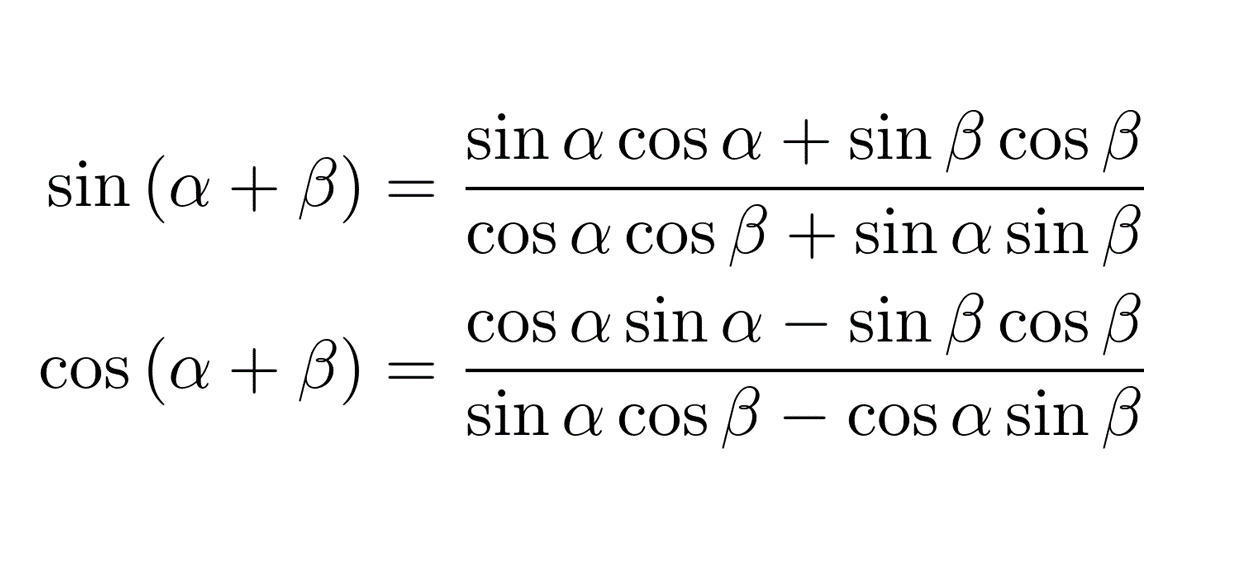
数学教室和(なごみ)講師の松中です。

和(なごみ)の講師は有志で常時いくつかの数学ゼミを定期的に開催しています。現在開講しているのは以下の4つです。
・ゲージ理論(今のところほとんどはリーマン幾何)
・微分幾何(ちょっと前までは素粒子物理をやっていた)
・多変量解析
・リーマン面

私は現在、ゲージ理論とリーマン面のゼミに参加しているのですが、リーマン面のゼミの中で今まで見たことのなかった三角関数の加法定理を発見したので、ご報告させていただきます。

加法定理

加法定理とは高校で学ぶ三角関数の公式です。

　
加法定理の覚え方はいろいろあるみたいですが、私は
・$\sin$は$\sin\cos$、$\cos$は$\cos\cos$、後半はその逆
・$\alpha$、$\beta$の順番はそのまま
・$\cos$の方は符号が逆になる
と、断片的なルールで覚えました。

私は高校時代に覚えようと意識して覚えた公式はこれだけだと思います。他の公式は、形が単純だったり、意味を考えれば明らかだったり、という理由で使っているうちに自然に覚えられるものと、複雑すぎるから覚えるのをあきらめて定義や他の公式から導出すると決めたものに分けられます。

加法定理はそれなりに複雑な上、$\cos$、$\sin$の定義や他の公式から導出するには少し手間であるため意識的に覚えました。余談ですが、東京大学の入試問題には「加法定理を証明せよ」という問題が出たことがあります。東京大学を受ける方であれば加法定理は当たり前に使いこなしているはずですが、いざ証明しろと言われると難しいのかもしれませんね。

$\cos$の別の定義

さて、リーマン面のゼミでは「リーマン面の理論」というテキストを読んでおり、第1章では$\cos$を高校とは異なる方法(代数的関数の積分の逆関数)で定義し、そのアナロジーで楕円関数を導入しています。本記事には関係はないのですが、こちらがこのテキストでの$\cos$の定義です。

　
同じ$\cos$なのに、いろいろな定義があって面白いです。ちなみに私が大好きな$\cos$の定義はこちらです。

　
円も、円らしき数式も出てこないこのシンプルな微分方程式で三角関数を定義できるとは驚きです。なんとこの定義をすると$\pi$の定義はこうしてもよいことになります。

$$\pi\equiv\inf\left\{\theta>0|s(\theta)=0\right\}$$
通常$\pi$は直径と円周の長さの比で定義されるため「円周率」と呼ばれますが、それは$\pi$が持つたくさんの顔の1つに過ぎないのでしょう。

話がそれましたが、テキストではその後、楕円関数の加法定理を導くために、$\cos$の加法定理の証明のアイディアを述べています。その方法も高校で一般に習う方法とは異なるもので、円周上の点の運動に注目しています。

元々のアイディアは高校数学+α(物理、微分方程式)なのですが、実際に行う計算自体は高校数学で簡単にできるものです。加法定理は高校時代からよく知っているので、詳細に立ち入らず飛ばすこともできたのですが、ゼミということもありせっかくだから計算してみました。

当たり前の加法定理が当たり前に出てくるだけ。軽い気持ちでほとんど機械的に計算を続けていたのですが、どうしてもよく知っている加法定理が出てきません。何度計算しても、です。そこで気づきました、これは今まで見たことのない加法定理なのだと、、、

見たことない加法定理の導出

それではテキストのアイディアに沿ってこれまで見たことのなかった加法定理を導出しましょう。

図のように$xy$平面上に原点$O$を中心とする半径$1$の円$O$を用意します。$(1,0)$を$P$とし、$\angle{AOP}=\alpha$、$\angle{BOP}=\beta$となる円周上の点$A$、$B$をとります。次に、点$P$を通り直線$AB$に平行な直線と円$O$の2つの交点のうち、$P$と異なる方を$Q$とします。

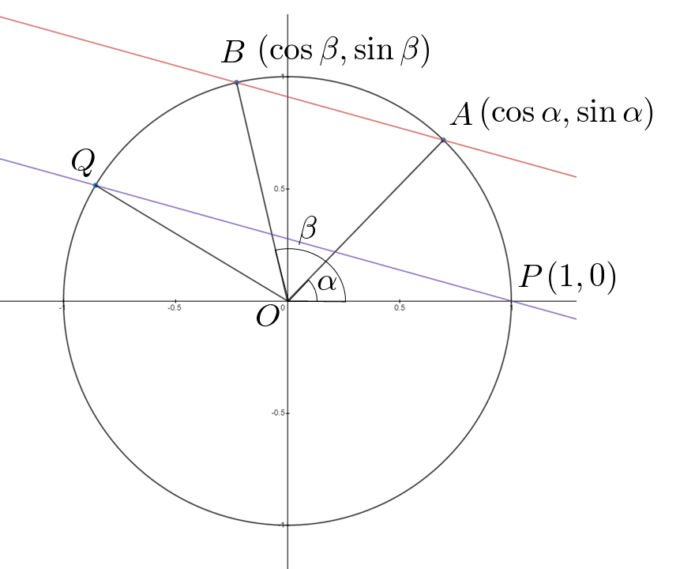
$\angle{QOB}=\alpha$の証明

まず、$\angle{QOB}=\alpha$となることが以下のように示せます。

直線$PQ$と線分$OA$、$OB$の交点をそれぞれ$S$、$T$とし、$\triangle{OPT}$と$\triangle{OQS}$が相似(合同ではあるがそこまで示す必要はない)であることを示します。$\triangle{OPQ}$は$OP=OQ$の二等辺三角形より、$\angle{OPT}=\angle{OQS}$(①)です。また、$\triangle{OAB}$は$OA=OB$の二等辺三角形より$\angle{OAB}=\angle{OBA}$となり(簡単のためこの角度を$\gamma$と置きます)、直線$AB$と直線$PQ$が平行であることから、同位角より$\angle{OTP}=\angle{OSQ}=γ$(②)が分かります。①、②より2角が等しいことから$\triangle{OPT}$と$\triangle{OQS}$が相似であることが示され、$\angle{POT}=\angle{QOS}$となります。よって、$\angle{QOB}=\angle{POQ}-\angle{POT}=\angle{POQ}-\angle{QOS}=\alpha$であることがわかります。

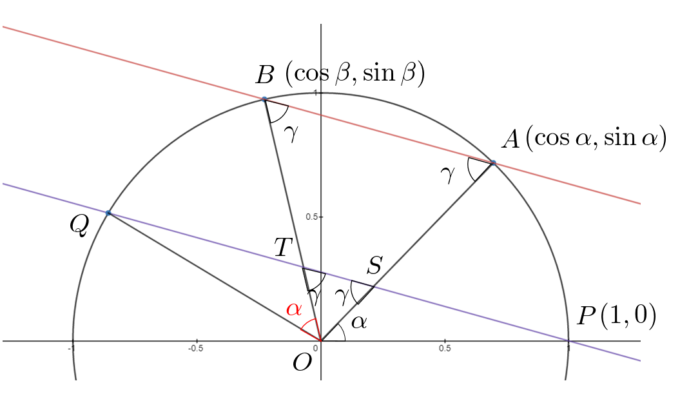
※$\alpha$、$\beta$の取り方によってはここでの議論がそのまま成り立たなくなりますが、本質的な問題ではありません。また、例えば$\alpha=\pm\beta$の時は直線ABが引けなかったり、$y$軸と平行になってしまって傾きが定義できなかったり、いろいろ問題がありますが、この後の議論ではそのような特別の場合は考えていません。別途議論すればよいだけです。

見たことのない加法定理の導出

以上で$\angle{QOP}=\alpha + \beta$であることが分かったので、$Q$の座標は$(\cos{(\alpha + \beta)},\sin{(\alpha + \beta)})$であることが分かります。よって$A$、$B$の座標から代数的に$Q$の座標を求めることで加法定理が得られそうです。

$AB$を通る直線は、$P$を通り傾きが$(\sin{\beta}-\sin{\alpha})/(\cos{\beta}-\cos{\alpha})$であることから、

$$y=\frac{\sin{\beta}-\sin{\alpha}}{\cos{\beta}-\cos{\alpha}}(x-1)$$
と表せます。これと円$O$の方程式$x^2+y^2=1$を連立させると、
$$x^2+\left\{\frac{\sin{\beta}-\sin{\alpha}}{\cos{\beta}-\cos{\alpha}}(x-1)\right\}^2=1$$
と、一見計算が面倒に感じる二次方程式が出てきますが、$P$も交点の1つのため、これは$x=1$を解に持ちます。よって以下のように変形して$x-1\neq 0$で両辺を割ることで$Q$の$x$座標を得ることができます。

$$\left(\frac{\sin{\beta}-\sin{\alpha}}{\cos{\beta}-\cos{\alpha}}\right)^2(x-1)^2=-(x-1)(x+1)\\ \qquad\\ \left(\frac{\sin{\beta}-\sin{\alpha}}{\cos{\beta}-\cos{\alpha}}\right)^2(x-1)=-x-1\\ \qquad\\ x=\frac{(\sin{\beta}-\sin{\alpha})^2-(\cos{\beta}-\cos{\alpha})^2}{(\sin{\beta}-\sin{\alpha})^2+(\cos{\beta}-\cos{\alpha})^2}$$
同様に、$y$座標も
$$y=\frac{-2(\sin{\beta}-\sin{\alpha})(\cos{\beta}-\cos{\alpha})}{(\sin{\beta}-\sin{\alpha})^2+(\cos{\beta}-\cos{\alpha})^2}$$
となります。

$Q$の$x$座標は$\cos{(\alpha+\beta)}$、$y$座標は$\sin{(\alpha+\beta)}$であることから、右辺を展開して、以下の見たことのない加法定理が得られます。

「見たことのない加法定理」の変形

「見たことのない加法定理」が得られましたが、形が複雑です。最初にこれを見たとき、変形すれば高校で習う加法定理になるはずだと式変形を続けたのですが、結果「綺麗な見たことのない加法定理」を得ることができました。(通常の加法定理も得ることはできました。)

「見たことのない加法定理」の$\sin{(\alpha+\beta)}$の右辺の分子の最初の2つの項である$\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$は通常の加法定理により$\sin{(\alpha+\beta)}$であることが分かります。ずるいですが、ここを$\sin{(\alpha+\beta)}$と置き換えて、式変形をしてみましょう。

この最後の式で$\alpha\rightarrow \pi/2-\alpha$、$\beta\rightarrow -\beta$と置き換え、一般に$\sin{(\pi/2-x)}=\cos{x}$、$\cos{(\pi/2-x)}=\sin{x}$が成り立つことに注意すると、以下のように「綺麗な見たことのない加法定理」を得ることができます。パチパチパチ。

　
別の方向で式変形を続けると、以下のような「綺麗な見たことのない加法定理パート2」も作ることができました。

まとめ

今回は「見たことのない加法定理」を紹介させていただきました。もちろんこれらは通常の加法定理に比べて「見た目」も「使い勝手」も悪いです。これらの加法定理は分数になってしまっているため、分母が$0$になる場合は使うことができません。直線$AB$が定義できない場合や、$y$軸と平行になる場合を無視して議論を進めてきたツケが回ってきた形となります。

加法定理は(慣れてしまえば)とてもシンプルで、他の表示はないと本能的に思い込んでいましたが、今回紹介したようにある程度は綺麗な別の形でも表すことができるというのはとても驚きでした。$\sin$、$\cos$のような三角関数には相互に様々な関係式があり、それらの関係式が複雑に絡み合っているからこその結果だろうと思います。

コンピュータに三角関数の相互関係の式を与えて、機械的に式変形をさせまくって、次々に見たことのない加法定理を生成させたら面白いだろうなとは思いましたが、それはまた別の機会にします。

<文/松中>

参考)ゼミで読んでいる「リーマン面の理論」 寺杣友秀 (著) 森北出版