こんにちは。和からの数学講師の岡本です。みなさんは数列ってご存じですか？その字のままですが、「数の列」の事を言います。高校数学（数学ⅡB）で登場する分野で、苦手意識のある方も多いかもしれません。しかし、現価計算やデータ分析などの中で何かと登場し、多方面で応用されています。特に「極限」という概念は非常に重要で、数列の話題と密接に関係してきます。例えば次のような数列\(a_n\)を考えます。

\begin{align*}a_n=\frac{1}{n}\end{align*}

つまり、\(n=1\)のとき\(a_1=1/1\)、\(n=2\)のとき\(a_2=1/2\)、\(n=3\)のとき\(a_3=1/3\)となります。例えば、\(n=100\)のときは\(a_{100}=1/100\)となり、非常に小さい数となるのです。それではここで問題です。\(n\)を無限に大きくしていくとき、数列\(a_n\)はどんな値に近づくでしょうか？

答えは「ゼロ」です。注意していただきたいのは、「ゼロになる」のではなくて「ゼロに限りなく近づく」ということ。たとえどんなに大きな\(n\)を持ってきても、\(a_n=1/n\)はゼロより大きな数です。今日はこの「限りなく近づく」という表現について詳しく解説していこうと思います。

今日はたびたび授業で扱う「\(\varepsilon\)-\(N\)論法」についてお話をしようと思います。この\(\varepsilon\)-\(N\)論法とは、大学で登場する、数列の極限のとらえ方です。

１．高校で習う「極限」

先ほどの数列\(a_n=1/n\)について考えましょう。「\(n\)を大きくする（\(n\)を\(\infty\)（無限大）に近づける）と\(a_n\)は\(0\)（ゼロ）に限りなく近づく」という状況は、高校で習う「極限」という概念を用いると、

\begin{align*}\lim_{n\to \infty}a_n=0\end{align*}

と表現することができます。“無限大”というのは数ではないので、具体的に\(n\)に「代入する」ということができません。つまり

\begin{align*}a_{\infty}=0\end{align*}

という表現は正確ではありません。あくまで、「\(n\)を大きくするときに限りなく近づく値」なので、この\(\lim_{n\to \infty}\)という記法は非常に理にかなっていますし、何かと便利です。例えば、こんな極限を考えてみましょう。

\begin{align*}\lim_{n\to \infty}\frac{2n}{3n+1}=?\end{align*}

数学Ⅲのテストででてきそうな問題です。このような「何に限りなく近づくか求める」タイプの問題は\(\lim_{n\to\infty}\)の使いやすさが身に沁みます。実際に計算するときは極限操作を行う前に式を整理します。例えば上の問題の場合、分母分子を\(n\)で割ることにより\(\lim_{n\to \infty}1/n=0\)という、先ほど出てきた極限に帰着します。

\begin{align*}\lim_{n\to\infty}\frac{2n}{3n+1}=\lim_{n\to \infty}\frac{2}{3+1/n}=\frac{2}{3+0}=\frac{2}{3}\end{align*}

この\(\lim\)という記号、計算上は確かに便利ですが、そもそも「限りなく近づく」ってどういう意味なのでしょうか？

２．「近づく」ってどういうこと？

「近い」という言葉を辞書で引くと「離れていないさま」と書かれています。つまり、「距離」という概念が必要になってきます。数直線上（実数）の世界の、点と点の距離は、「差（絶対値）」と考えるのが一般的です。この絶対値を使って次のような状況を考えます。

任意の実数\(\varepsilon>0\)に対して、ある自然数\(N\)が存在し、

\begin{align*}n\geq N \Rightarrow |a_n-\alpha|<\varepsilon\end{align*}

驚くべきことに、これが\(a_n\)が\(\alpha\)に「限りなく近づく」ということの厳密な表現になっているのです！

３．イプシロン・バリア―！！

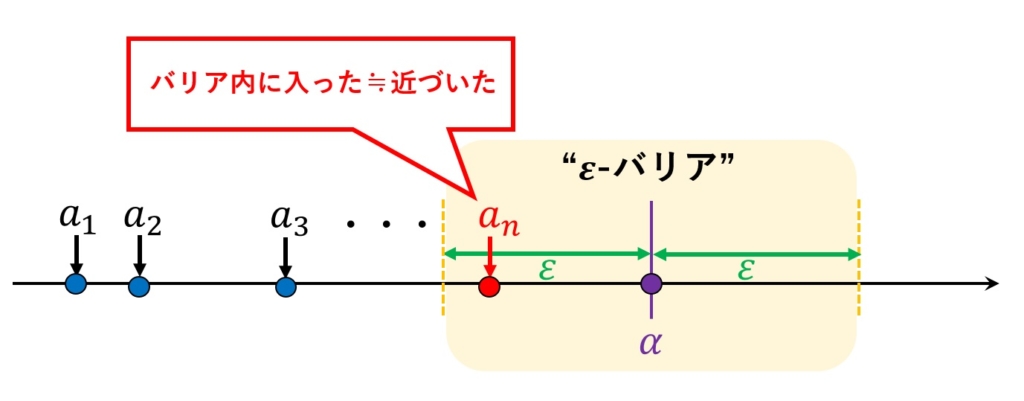
上述した式の意味を説明しましょう。まず「任意の」という言葉は数学で非常によく使われる頻出用語です。これは「どんな～」とか「勝手な～」といった意味です。つまり、「任意の実数\(\varepsilon>0\)に対して」とは「どんな正の実数\(\varepsilon\)に対しても～」という意味です。数列\(a_n\)が「\(\alpha\)に近づく」ということを、差\(|a_n-\alpha|\)が\(\varepsilon\)未満になると表現します。つまり、収束するであろう実数\(\alpha\)の周りに“\(\varepsilon\)バリア”を張ったとします。このバリア内に数列\(a_n\)が入り込んでくることを「近づく」と表現したいのです。

４．「限りなく近づく」とは

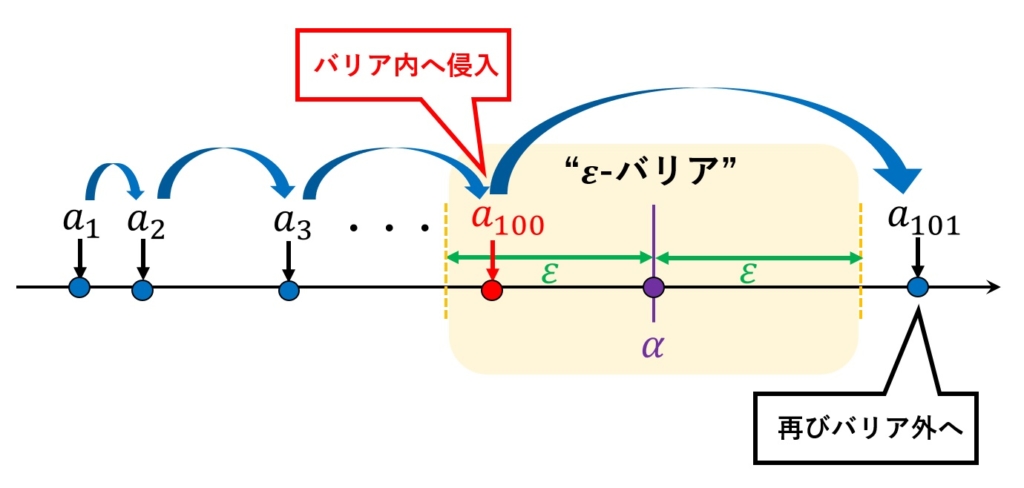
３節では、「\(\varepsilon\)バリア内に数列\(a_n\)が入ること」が、おおよそ「近づくこと」という説明でした。しかし、一度でもバリア内に数列が入ってきたら「近づいた」と言ってもいいのでしょうか？例えば、\(a_{100}\)で初めてバリア内に侵入してきたものの、\(a_{101}\)で再びバリア外に出ていったとしましょう。この場合、「真に近づいた」とは言えません。

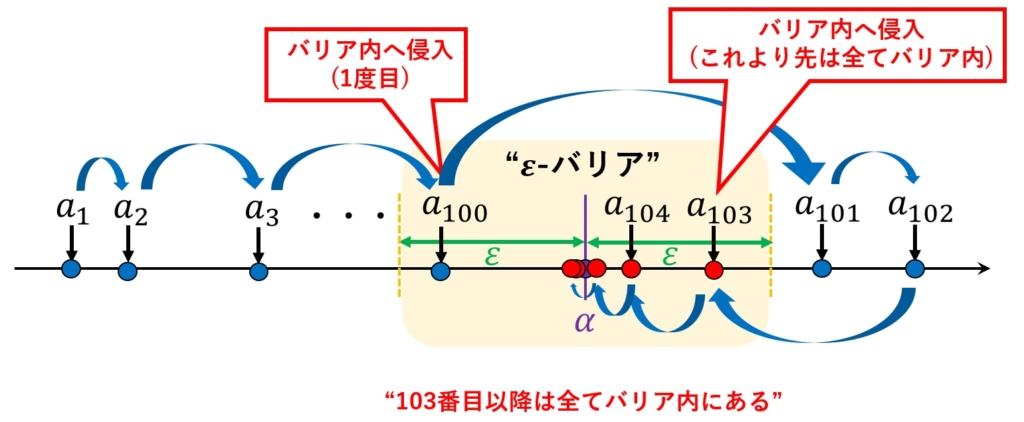
そこで、「真に近づく」ということをそれ以上先の数列全てがバリア内に入ることと考えることにします。例えば次の図のように「１０３番目以降は全てバリア内にある」というとき、数列\(a_n\)は\(\alpha\)に「真に近づく」といことになります。

しかし、これではやや不十分です。なぜかというと、上の例の「103番」というのはバリアの貼り方に依ります。つまり、\(\varepsilon\)の大きさに依存するのです。そこで、「どんな\(\varepsilon\)にも対応できる」＝「どんなバリアを張っても、必ずその先バリア内に入り続ける番号\(N\)が存在する」という状況を考えます。これはつまり

任意の実数\(\varepsilon>0\)に対して、ある自然数\(N\)が存在し、

\begin{align*}n\geq N \Rightarrow |a_n-\alpha|<\varepsilon\end{align*}

ということであり、これが「限りなく近づく」ということなのです。以上が「\(\varepsilon\)-\(N\)論法」の全てです。

せっかくなので、\(\varepsilon\)-\(N\)論法を使って、\(a_n=\frac{1}{n}\)が\(0\)に限りなく近づくことを証明してみましょう。
まずはテキトーに実数\(\varepsilon>0\)を取ってきます。このとき、\(N\)を

\begin{align*}N:=\left[\frac{1}{\varepsilon}\right]+1\end{align*}

で設定します。ここで\([x]\)とは、実数\(x\)の整数部分を表します（例えば\([3.14]=3\)）。すると\(n\geq N\)を満たす\(n\)について

\begin{align*}|a_n-0|=\frac{1}{n}\leq \frac{1}{N}=\frac{1}{[\frac{1}{\varepsilon}]+1}<\frac{1}{\frac{1}{\varepsilon}}=\varepsilon\end{align*}

となり、\(\varepsilon\)-バリア内に入っていけます（実はバリア内に入っていけるように逆算して\(N\)を設定するのです）。これはどんな\(\varepsilon\)に対しても同じ作戦でバリア内に侵入できるので、「\(a_n\)は0に限りなく近づく」と言えるのです。

５．さいごに

いかがでしたでしょうか。大学初年度に理系（特に数学専攻）の学生の大多数がつまずいてしまう「\(\varepsilon\)-\(N\)論法」。式だけ見ても一見意味不明のようですが、１つひとつの意味を見ていくと、非常に自然な考え方であることがわかります。数学とは、このような細かいですが「厳密なとらえ方」の上に成り立っています。まさに人類が築き上げてきた叡智なのです！オススメの書籍としてはまず

イプシロン・デルタ論法 完全攻略 原 惟行 (著), 松永 秀章 (著) 共立出版

数研講座シリーズ 大学教養 微分積分　加藤 文元 (著)数研出版
では詳しい演習問題付きで学習に最適です。

また、名著「微分積分学Ⅰ」

では非常に分かりやすく丁寧に解説されてあり、教科書としてもオススメです。

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>