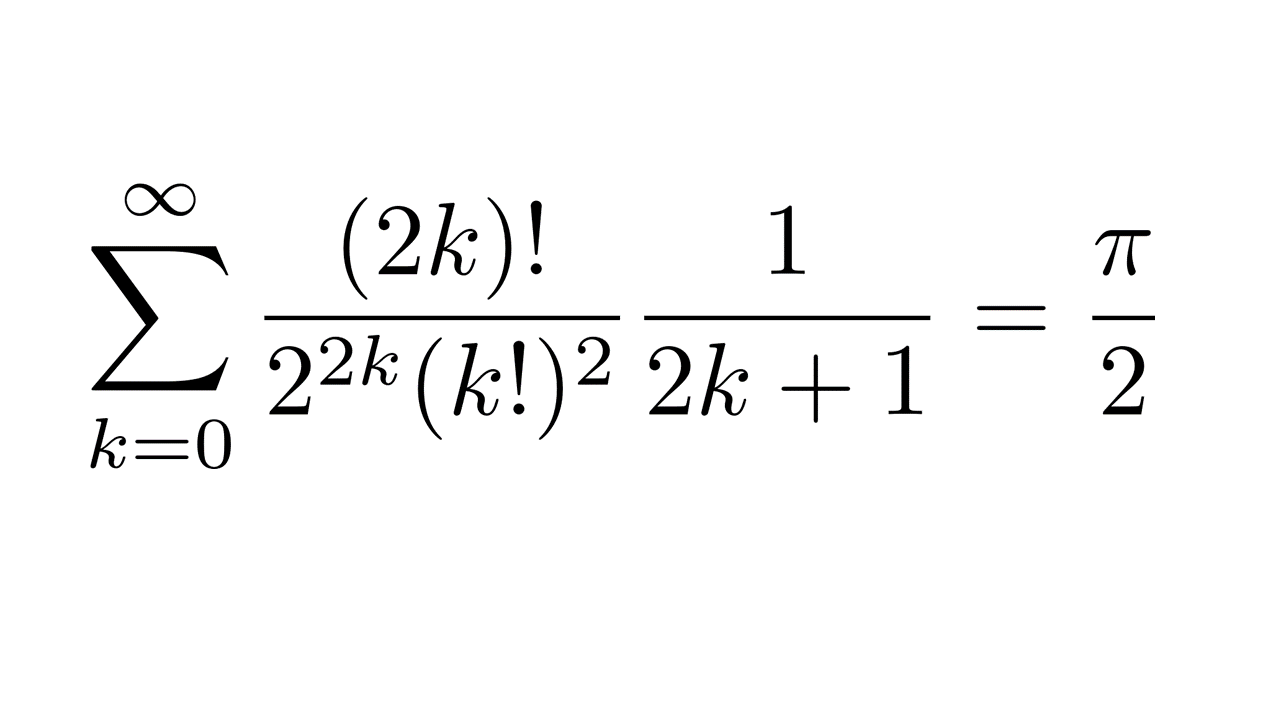やばそうな数式(総乗の証明編)~キラキラ数学プロジェクト~
公開日
2020年10月6日
更新日
2020年10月6日
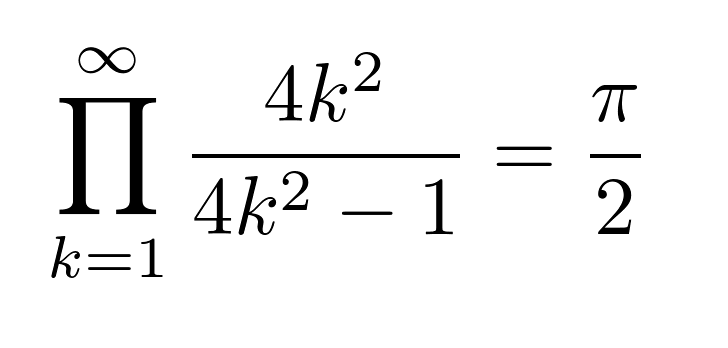
数学教室和(なごみ)講師の松中です。
先日やばそうな数式を紹介させていただきました。
やばそうな数式は分けて書くと、
\[
\begin{align*}
\left( \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx \right)^2 &=\frac{\pi}{2}\\\\
\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} &=\frac{\pi}{2}\\\\
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1} &= \frac{\pi}{2}
\end{align*}
\]
という3つの等式から成っています。上から積分、総和、総乗と名付けていましたので、今回の記事から3本に分けてそれぞれ証明します。
本当は数学の世界のはるか上空の視点からこの3つの等式を統一的に証明したかったのですが、それは叶わず、それぞれ異なる手法で証明を行いました。
証明の難易度ですが、総乗が高校レベル、総和が大学一年(微積)レベル、積分が大学二年(複素関数)レベルになっています。レベル順ということで総乗、総和、積分の順番に証明していきます。本記事は総乗の等式の証明になります。証明は高校の数Ⅲの微積まで学んだ方であれば十分式を追いかけていけると思います。
証明
証明の流れ
今回証明する総乗の等式はこちらです。
\[
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1} = \frac{\pi}{2}
\]
最初は気付かなかったのですが、これは以下のように変形すると、有名なウォリスの公式そのものであることが分かりました。
\[
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1} = \prod_{k=1}^{\infty} \left(\frac{2k}{2k – 1}\cdot\frac{2k}{2k + 1}\right) = \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots=\frac{\pi}{2}
\]
ということで、ウォリスの公式の証明を追っていきましょう。証明したい等式に\(\infty\)が出てきているのは少し嫌なので、以下のように書き換えます。
\begin{align*}
&\prod_{k=1}^{\infty} \left(\frac{2k}{2k – 1}\cdot\frac{2k}{2k + 1}\right)=\lim_{n\rightarrow \infty}\prod_{k=1}^{n} \left(\frac{2k}{2k – 1}\cdot\frac{2k}{2k + 1}\right)\\\\
&=\lim_{n\rightarrow \infty}\left(\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots\frac{2n}{2n-1}\cdot \frac{2n}{2n+1}\right)
\end{align*}
\(\lim\)の中身の
\[
\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots\frac{2n}{2n-1}\cdot \frac{2n}{2n+1}
\]
を次式で定義する\(I_n\)を用いて表し、\(n\rightarrow \infty\)とすることで目的の数式を証明します。
\[
I_n=\int_0^\frac{\pi}{2}\sin^n{x}dx
\]
\(I_n\)を計算する
\(I_n\)の値を実際に求めましょう。\(n\geq 2\)のとき、部分積分を用いると
I_n&=\int_0^\frac{\pi}{2}\sin^n{x}dx=\int_0^\frac{\pi}{2}\sin{x}\sin^{n-1}{x}dx\\\\
&=\left[ -\cos{x}\sin^{n-1}x \right]^{\frac{\pi}{2}}_0+\int_0^\frac{\pi}{2}\cos{x}\times (n-1)\sin^{n-2}{x}\cos{x}dx\\\\
&=(n-1)\int_0^\frac{\pi}{2}\sin^{n-2}{x}\cos^2{x}dx\\\\
&=(n-1)\int_0^\frac{\pi}{2}\sin^{n-2}{x}(1-\sin^2{x})dx\\\\
&=(n-1)\int_0^\frac{\pi}{2}\sin^{n-2}{x}dx-(n-1)\int_0^\frac{\pi}{2}\sin^{n}{x}dx\\\\
&=(n-1)I_{n-2}-(n-1)I_n
\end{align*}
となり、これから、\(nI_n=(n-1)I_{n-2}\)を経て、
\[
I_n=\frac{n-1}{n}I_{n-2}
\]
がわかります。
この漸化式を使うことで\(I_n\)が求まります。
実際、\(\displaystyle I_0=\int_0^\frac{\pi}{2}dx=\frac{\pi}{2}\)から、
I_{2n}&=\frac{2n-1}{2n}I_{2n-2}=\frac{2n-1}{2n}\cdot\frac{2n-3}{2n-2}I_{2n-4}\\\\
&=\cdots=\frac{2n-1}{2n}\cdot\frac{2n-3}{2n-2}\cdots \frac{3}{4}\cdot\frac{1}{2}I_{0}\\\\
&=\frac{2n-1}{2n}\cdot\frac{2n-3}{2n-2}\cdots \frac{3}{4}\cdot\frac{1}{2}\times\frac{\pi}{2}
\end{align*}
が、\(\displaystyle I_1=\int_0^\frac{\pi}{2}\sin{x}dx=1\)から、
I_{2n+1}&=\frac{2n}{2n+1}I_{2n-1}=\frac{2n}{2n+1}\cdot\frac{2n-2}{2n-1}I_{2n-3}\\\\
&=\cdots=\frac{2n}{2n+1}\cdot\frac{2n-2}{2n-1}\cdots\frac{4}{5}\cdot \frac{2}{3}I_{1}\\\\
&=\frac{2n}{2n+1}\cdot\frac{2n-2}{2n-1}\cdots \frac{4}{5}\cdot\frac{2}{3}
\end{align*}
となります。\(n\)が偶数の時と奇数の時で若干表示は変わりますが、\(I_n\)を求めることができました。
\(\lim\)の中身を\(I_n\)を用いて表す。
\(\lim\)の中身、\(I_{2n}\)、\(I_{2n+1}\)をそれぞれ並べて書いてみます。ただし\(I_{2n}\)、\(I_{2n+1}\)は先に示した分数の掛け算の順番を変えています。
\lim\text{の中身}&=\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdots\frac{2n}{2n-1}\cdot \frac{2n}{2n+1}\\\\
I_{2n}&=\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{5}{6}\cdots \cdot\frac{2n-3}{2n-2}\cdot \frac{2n-1}{2n}\times \frac{\pi}{2} \\\\
I_{2n+1}&=\frac{2}{3}\cdot\frac{4}{5}\cdot\frac{6}{7}\cdots \cdot\frac{2n-2}{2n-1}\cdot \frac{2n}{2n+1}
\end{align*}
並べてみると、\(I_{2n}\)の分母と分子を逆にした
\frac{1}{I_{2n}}=\frac{2}{1}\cdot\frac{4}{3}\cdot\frac{6}{5}\cdots \cdot\frac{2n-2}{2n-3}\cdot \frac{2n}{2n-1}\times \frac{2}{\pi}
\]
と\(I_{2n+1}\)を掛けると\(\lim\)の中身が出てくることが分かります。
つまり、
\[
\lim\text{の中身}=\frac{I_{2n+1}}{I_{2n}}\times\frac{\pi}{2}
\]
となっています。
\(\lim\)の中身を不等式で評価する
ここで、\(\displaystyle 0< x<\frac{\pi}{2}\)の範囲で\(0<\sin{x}<1\)なので、\(n< m\)なら\(\sin^n{x}>\sin^m{x}>0\)となり、これから、
\[
0 < I_{2n+2} < I_{2n+1} < I_{2n}
\]
が成り立つことがわかります。
次に、\(\displaystyle \frac{I_{2n+2}}{I_{2n}}=\frac{2n+1}{2n+2}\)と、\(\displaystyle \frac{I_{2n+1}}{I_{2n}}=(\lim\text{の中身})\times\frac{2}{\pi}\)に注意して、不等式の各辺を\(I_{2n}>0\)で割ると、
\[
0<\frac{2n+1}{2n+2}< (\lim\text{の中身})\times\frac{2}{\pi} < 1
\]
となります。
ここで、\(n\rightarrow \infty\)の極限を考えると、
\[
\lim_{n\rightarrow \infty}\frac{2n+1}{2n+2}=1
\]
より、はさみうちの原理から
\[
\lim_{n\rightarrow \infty}(\lim\text{の中身})\times\frac{2}{\pi}=1
\]
がわかるので、結局総乗の等式、
\[
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 - 1} = \lim_{n\rightarrow \infty}\prod_{k=1}^{n} \left(\frac{2k}{2k - 1}\cdot\frac{2k}{2k + 1}\right)=\frac{\pi}{2}
\]
が証明されました。
まとめ
今回はやばそうな数式の総乗の等式を証明しました。早めにウォリスの公式であることに気づけたので、証明ができましたが、ウォリスの公式を知らないと自力でこの証明を見つけ出すことは難しいのではないかと思います。ゼロから自分で証明を見つけるのは難しくても、証明を追うことはできると思いますので、是非紙とペンを片手に自分の手で証明を再現してみてください。次回は総和の等式の証明です。大学数学で学ぶテイラー展開が役に立ちます。お楽しみに!
<文/松中>