海難から人々の命を救った数学-対数の発見-
公開日
2020年7月12日
更新日
2020年7月12日

↓↓↓動画で見たい方はこちら↓↓↓
みなさん、今回は「数学はなんのためにあるか」を考える内容をお伝えしたいと思います。
学生の皆さんは今まさに「意味がよく分からない公式をたくさん覚えさせられて、計算や証明をひたすら解かされて、何の意味があるのか」と憤っていることろかもしれません。社会人の方も意外な場面で数学に直面して、困り果てている方もいるかもしれないですね。
数学の言葉の一つである対数もその一つだと思います。「ログ」という名前で覚えている人も多いでしょう。教科書には次のような式が書いてあって、「指数関数の逆関数」などと書いてあったりします。
指数関数:\(2^3=2×2×2=8\)
対数関数:\(3=\log_2 8\)
こんな式を見せられて、「なんのために使うのか、そもそも指数関数もよく分からない」と感じるのも無理はありません。分からないを大切に、和から。今日は、そんな「対数」についてお話ししていこうと思います。
この記事の主な内容
1. 対数はいつ生まれたのか?
対数が誕生したのは、1614年のことです。時は大航海時代、ヨーロッパ各国が新天地に向けて広大な海に船を漕ぎ出した頃、スコットランドの数学者、ジョン・ネイピアによってもたらされました。ジョン・ネイピアは、敬虔なプロテスタントでスコットランドのバロン(貴族の称号です)で、天文学や数学にも明るい学者でもありました。

ジョン・ネイピア(1550-1617)
大航海時代で新天地を求めて次々に船を出しますが、当時は非常に遭難、沈没など海難事故が多かったのです。というのも航海の間、海の上には目印になるものはありません。移動距離が長いため、ほんの少し角度がずれただけで目的地にたどり着くことはできなくなります。そのため自分の位置を正確に把握するためには、三角法と呼ばれる計算を行なっていました。自分の船の正確に測位を計算するために、天文学者が動員されて三角関数を駆使して計算を求めていました。三角関数は、いわゆるサイン、コサインと呼ばれているものです。
$$\tan{\frac{A+B}{2}}=\frac{\cos{\frac{a-b}{2}}}{\cos{\frac{a+b}{2}}}\cot{\frac{C}{2}}$$
こちらの基本公式には、\(\cos\)、\(\tan\)、\(\cot\)と、三角関数の計算がたくさん出てきます。この結果から航路を決めるわけですが、少しでも計算結果がずれれば目的地には決してたどり着けません。無事に到着するためには、10桁以上の計算精度が必要でした。つまり、当時の航海の成否はこの計算によって決まったと言っても過言ではなく、船が生還して国に戻れるかどうかを分ける非常に役目だったのです!
今ではGoogle Mapなどでお馴染みの、全方位測位システム(GPS)などあるはずもなく、計算を誤ったら目的地にたどり着かないまま食料が尽きるか、見知らぬ土地に漂着するかのどちらかです。その計算ですが、高い精度で計算を行う上で困難を極めたのは、三角関数で大きい数のかけ算と割り算を行うことです。電卓やコンピューターもない時代、莫大な計算が乗船した天文学者に委ねられており、相当な負担であったと言われています。
そんな中ネイピアによって発明されたものが、大きな数でも精度を高く効率的に計算する、まさに魔法のような方法、それが対数です。ネイピアは信仰が非常に厚く、自身の発明を次のようなタイトルでまとめています。
Mirifici Logarithmorum Canonis Descriptio
英訳:Description of the wonderful canon of logarithms
日本語訳:奇跡の対数法則の記述
ロガリズム(logarithms)という言葉は、この時ネイピアによって考案された造語です。logos(神の言葉)とギリシャ語のarithmos(数)を合わせてlogarithmsという言葉を作りました。ネイピアは自らの著書を「奇跡」と呼びました。対数が「人の命を救う」だけの力を持っていると考えたためです。その後ネイピアは20年の歳月をかけて、三角関数の対数を8桁の精度で計算できる「対数表」を作成しました。この表によって、三角法の計算をより正確に、効率的に行うことができるようになったのです!
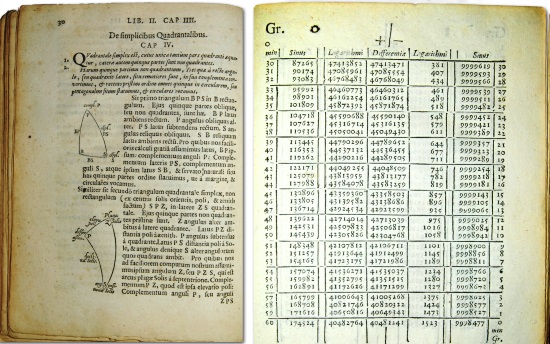
ネイピアが作成した対数表。三角関数の数値が8桁まで計算されている。
2. 対数の考え方
それではこの辺りで、対数の考え方について解説していきましょう。対数の考え方は非常にシンプルで、大きな数の掛け算を行うときに、結果の数字に注目するのではなく、「かけた回数」に注目する考え方です。
例えば、次の2つの会社の資本金を比較してみましょう。1つは弊社、もう1つは日本で最も資本金が高い日本郵政です。ちなみに弊社の資本金は、円周率(3.14…)が由来となっています!(笑)
和から株式会社:3,141,592円
日本郵政株式会社:3,500,000,000,000円
いずれも桁が大きく、パッと見て比べにくい数字ですね。みなさんはこの2つの数を比較するときに、どのように考えるでしょうか。
引き算する方法で比較することもできますが、多くの方は「桁数」を比べようとするのではないでしょうか。和から株式会社の資本金は7桁、日本郵政は13桁になるので、6桁差があると考えるわけですね。このように桁数を比較する考え方は、「10を何回かけたか」に注目しているのです!これを数式で書き表すと、次の式の通りになります。
\(\log_{10} {3,141,592} \simeq 6.5\)
\(\log_{10} {3,500,000,000,000} \simeq 12.5\)
それぞれ、「3,141,592円は10を6.5回かけると求められる」、「3,500,000,000,000円は10を12.5回かけると求められる」という意味になります。ここで、「6.5回かけるってどういう意味なのか?」ということが気になる方は、ぜひ対数を勉強してみてください。対数は数学史上最も後世に影響を与えた概念の一つです。対数を扱うことで、大きな数の計算が飛躍的に便利に行えるようになったのです。
3. 日常に現れる対数
対数は、日常に現れる数字にも表れています。例えば、地震の強さを表すマグニチュードと呼ばれる数字は、地震が発生するエネルギーの対数を取ることで算出されています。
$$\log_{10} E=4.8+1.5M$$
一つだけ計算してみると、エネルギーを使って「今日の地震は10,000,000,000,000(J:エネルギーの単位)でした。」とニュースで伝えられても数が大きすぎてよく分からないですね。その代わり、
\(\log_{10} 10,000,000,000,000=13=4.8+1.5M\)
\(13=4.8+1.5M\)
\(8.2=1.5M\)
\(M=5.4666\cdots\)
と計算して、「今日の地震はマグニチュード5.46です。」と伝えられた方がイメージしやすいわけですね。実はマグニチュード7と8は、数字の上では1しか変わりませんが、「10をかける回数が1.5回分違う」ということになるので、エネルギーだと約31倍異なる、となります。例えば阪神淡路大震災(1995)のマグニチュードが7.3、東日本大震災(2011)では9.0ですから、数字が2違いますので、「10をかける回数が3回分違う」、つまり約1,000倍のエネルギー差となります。いかに大きな地震であったかがよく分かりますね。他にも音の大きさを表すデシベル、酸性やアルカリ性の強度を表すpHなどにも活用されています。大きい数を扱う天文学をはじめ、気象学、データ分析、実に様々な分野に対数という概念は浸透しています。
終わりに
いかがだったでしょうか。大航海時代に発明された対数によって、海上の船の測位を正確に計算することができるようになりました。航海における遭難のリスクも大幅に低減され、計算にかかる負担も減らしたことから、後の大数学者で現代確率論の祖となったラプラスは「対数は天文学者の寿命を倍に延ばした」とコメントしています。ネイピアは他にも私たちが日常的に使用する小数点も発明しており、没後400年近く経ってなお現代を生きる私たちの生活にも密接に関わっています。
「数学をなぜ学ぶのか。」
学校で数学を教わるとき、社会人になって数学が必要な場面に直面するとき、何度となく考えたことがあると思います。数学を表す英語「mathematics」の語源になっているのはギリシャ語の「マテーマタ(mathemata)」、「学ばれるべきもの」です。対数を含めて、あらゆる数学が生まれたところには生活をよりよくするための思いが潜んでいます。数学がどう役立てられたか、日常のどこで使うのかを調べてみると、教科書の中で見る数学とはまた違った一面を見られるかもしれません。
数学について学んでみたい、どのように生活と結びついているのか知りたい、そんな方は和からにお越しください。無料の個別カウンセリングにて、皆様の学びたいことをお伺い致します。
ネイピアを含む色々な数学者のドラマを知ってみたいという方は、ぜひこちらもご覧ください!
面白くて眠れなくなる数学者たち 桜井 進 (著) PHP研究所















