ゲームの世界は丸いのか?~RPGから見るトポロジーの風景~
公開日
2020年2月4日
更新日
2020年2月4日
この記事の主な内容
1.RPGの世界地図
今回はゲームの世界を「トポロジー」と言われる数学的視点で考察していこうと思います。
ドラゴンクエストやファイナルファンタジーなどの、いわゆるRPG。プレーヤーの位置情報がわかるように、その世界における「世界地図(ワールドマップ)」というものがたいてい存在します(トップ画像のドット絵の主人公はオリジナルです。by 岡本)。
ゲーム内の地図では、主人公一行が右方向に進めば地図の左側から現れますし、上側に進めば主人公は下から現れます。
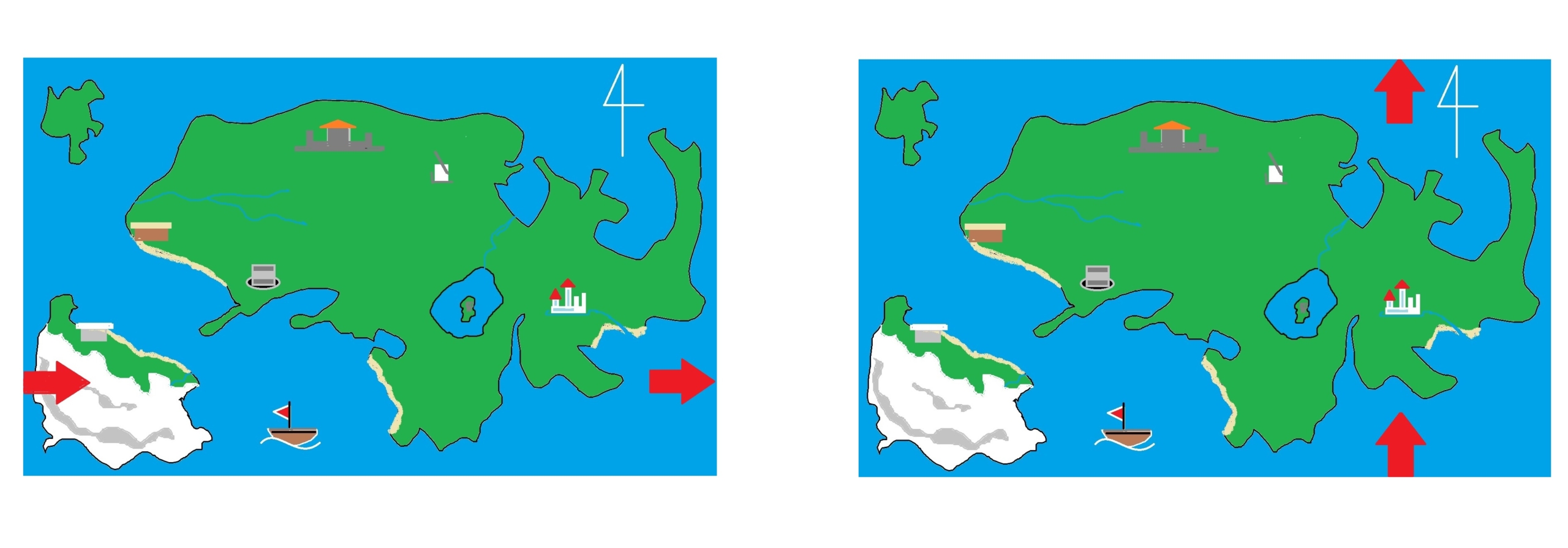
何もおかしなことはなさそうな気がしますが、実はすでに「おかしなこと」が起きています。
ゲーム内の地図におけるプレーヤーの動きに注目してみましょう。ゲームの世界は、下図のように縦方向に対応する黄色の矢印と、横方向に対応する赤色の矢印がこの向きで貼りあわされた世界であることになります。
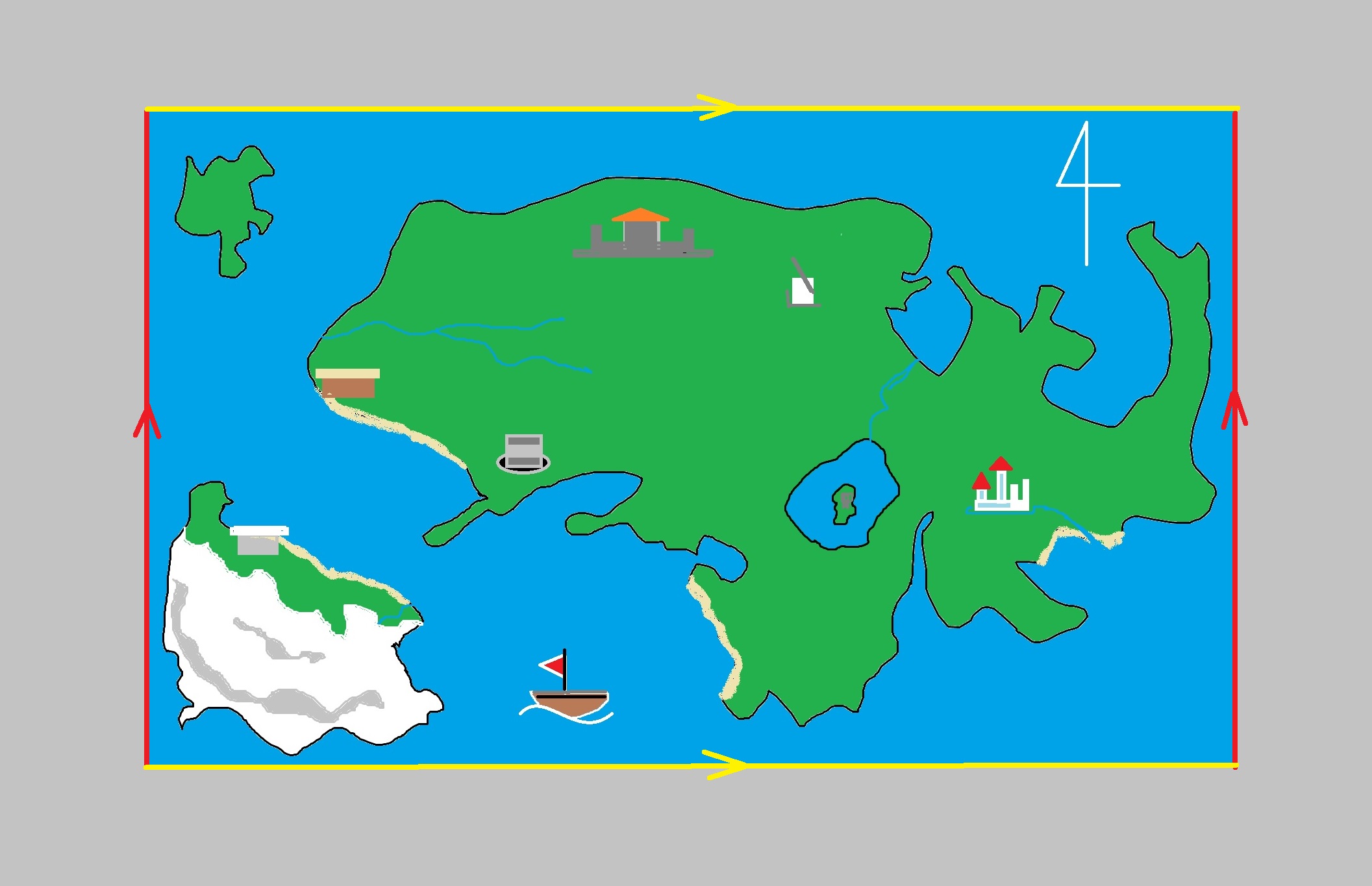
つまり、もしも主人公が巨人で、マップの境界線ギリギリのところに立っていたとすると、
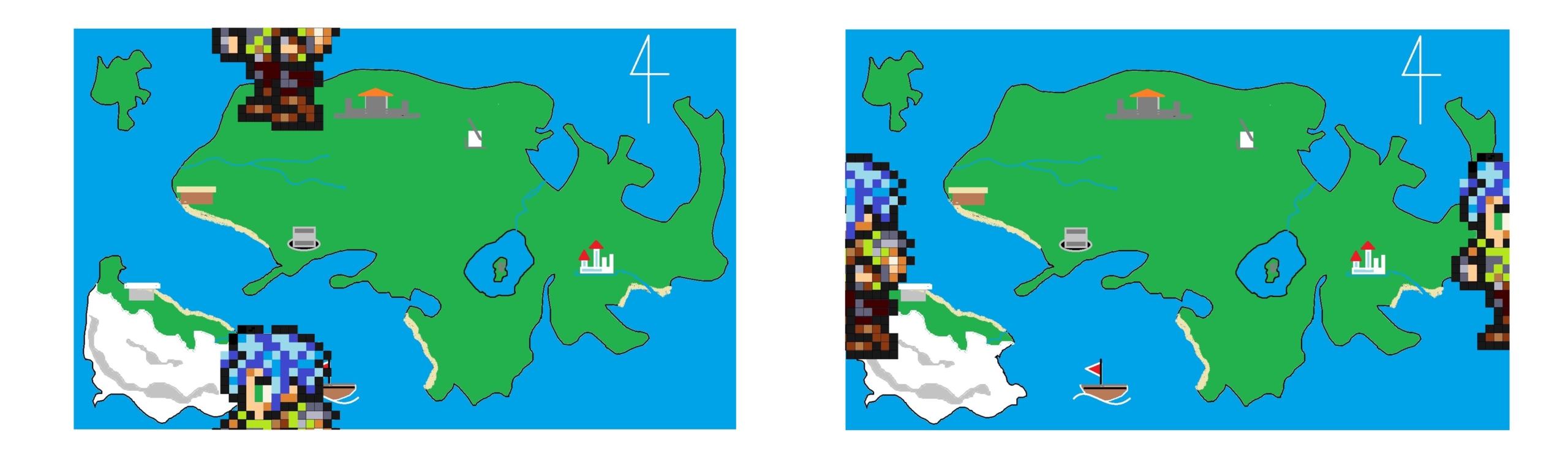
といった風になるはずです。この状況を矛盾なく表現しようとすると、まず縦方向に貼り合わせることになります。

続いて横方向のつながりに注目することで、下の図のように張り合わせることになります。

すると、なんということでしょう。主人公たちが冒険していた世界は、なんとドーナツ型になっていたことがわかります。

つまり、RPGの世界は私たちが住んでいる丸い地球と違い、穴の開いたドーナツ型の世界だったのです…!
2.そもそも球とドーナツ型って違うの?

地球のように丸い世界と、今回あらわになったRPGのドーナツ型世界。そもそもこういった2つの「形」はというのは“違う”ものなのでしょうか?
数学を使えば、この2つの形が異なるものであるということを「証明」することができます。

証明にはひたすら長いロープを使います。主人公にこれを持たせ、世界一周の大冒険に出かけてもらいます。
まず、スタート地点にロープの先端を固定します。こうして長いロープを地面に垂らしながら旅を始め、無事にスタート地点に戻ってくることで旅は終了します。さあ、大冒険に出かけましょう。

(参考:和から公式HP https://wakara.co.jp/)
山を越え、谷を越え、川を渡り、海を渡り、主人公は旅をします。
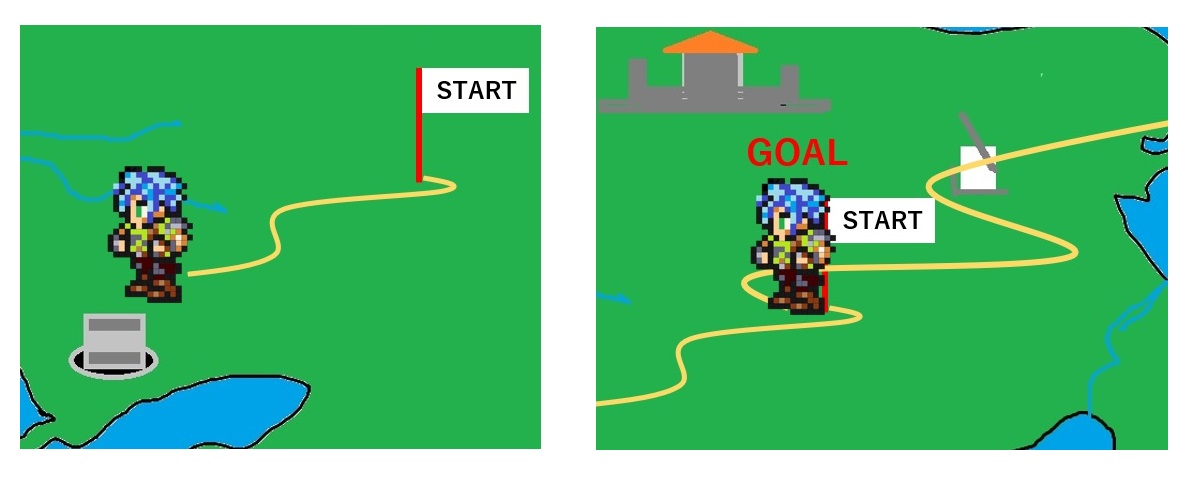
そして、最初のスタート地点に戻ってくることで、冒険は終了です。
さて、この後なにをするのかというと、世界中に垂らしてきたロープを手繰り寄せることで回収していきます(ただし、ロープは地表や海の表面から離れてはいけないものとし、簡単のため地面、海面には障害物は一切ないものとします)。
ここで重要なポイントは
もし世界が「球」であるならば、どんな冒険をしてもロープは必ず手元に戻ってくる。
という点です。ちょうど下の図のようなイメージです。
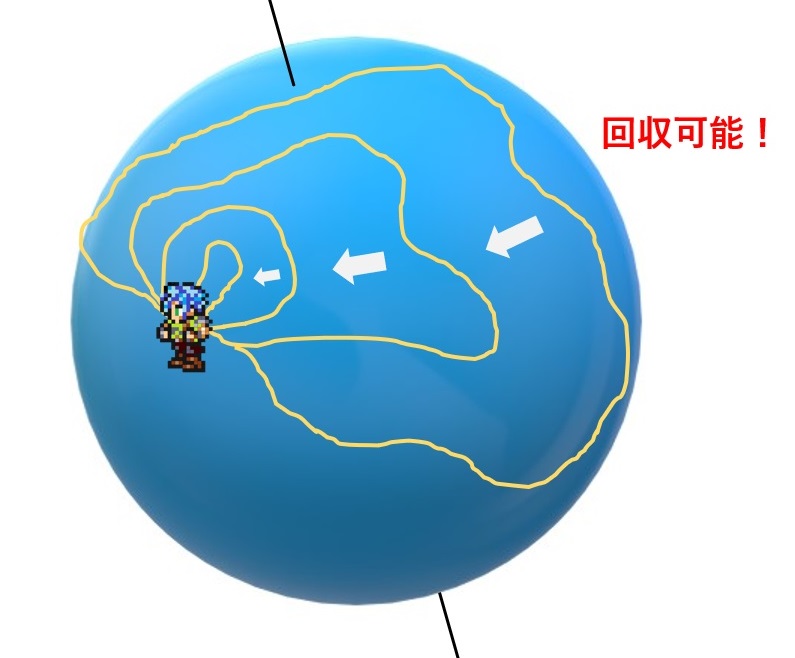
逆に手元にロープが戻ってこない(引っ掛かってもどってこない)ような冒険となった場合、その世界は球体ではないということになります!
では、ドーナツ型の世界ではどうなるでしょうか?もちろん次のようにロープを回収できる旅もあります。

しかし、例えばひたすら西に進む旅や、ひたすら北に進む旅をした場合、図のようにロープがひっかかってしまい、回収できないことになります。

このような構造の違いから、球とドーナツは「異なるもの」であることが証明できます。
こうした、長さにとらわれず、「穴が開いているかどうか」といった、非常に柔らかい視点で考える数学として「トポロジー」といわれる分野があります。トポロジーはデータ分析や数学アートの世界にも最近では応用されています。
次の章では、この「トポロジー」の考え方に慣れてもらうため、1つ面白い問題をご紹介します。
3.トポロジーマジック
この「柔らかさ」というのは、図形をゴムや粘土のように、連続的に変形させても構わないという感覚です。ただし決して切ったり貼ったりしてはならないというルールを課します。このルールのもとで、次のような問題を考えてみましょう。
問題 左の図を連続的に変形することで、右の図のような状態にできるでしょうか?

右の図は、輪が絡まっており、対して左の図は絡まりがほどけています。切り取って貼り付けない限り、輪の絡まりはほどけないような気がします。しかし、実は切ることも貼り付けることもなく、ゴムや粘土のように「連続的に変形」させることで、輪の絡まりをほどくことができるのです!まるでマジックのようですが、種も仕掛けもありません。
ではほどき方を解説していきましょう。
①まず片方の輪の付け根を矢印の方向に動かします。
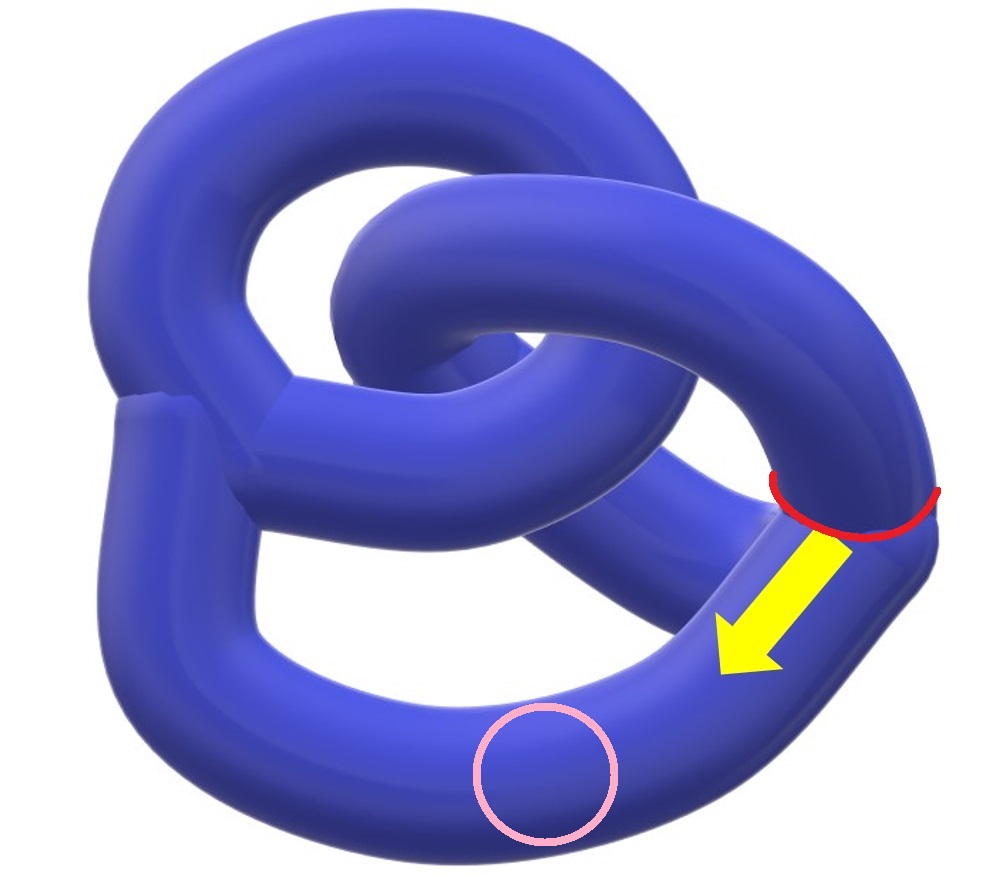
②付け根は、もう片方の輪の付け根に向けて移動させます。
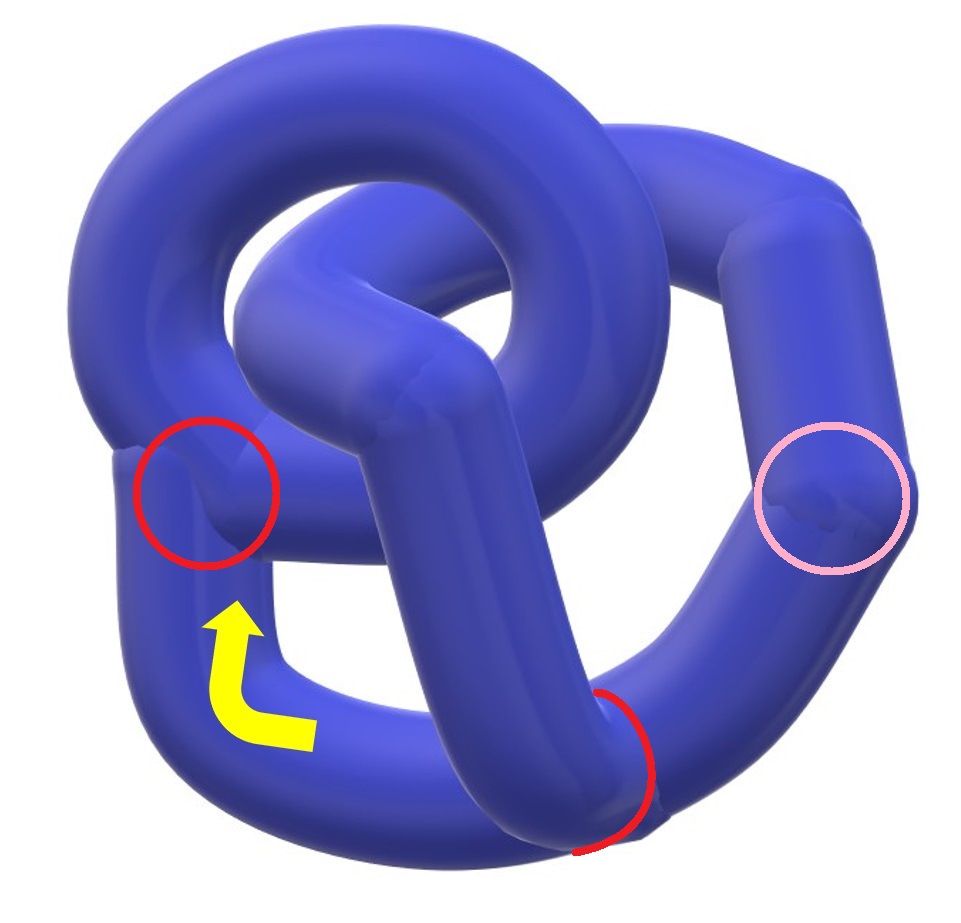
③付け根をもう片方の輪の中に通すようにして移動させます。
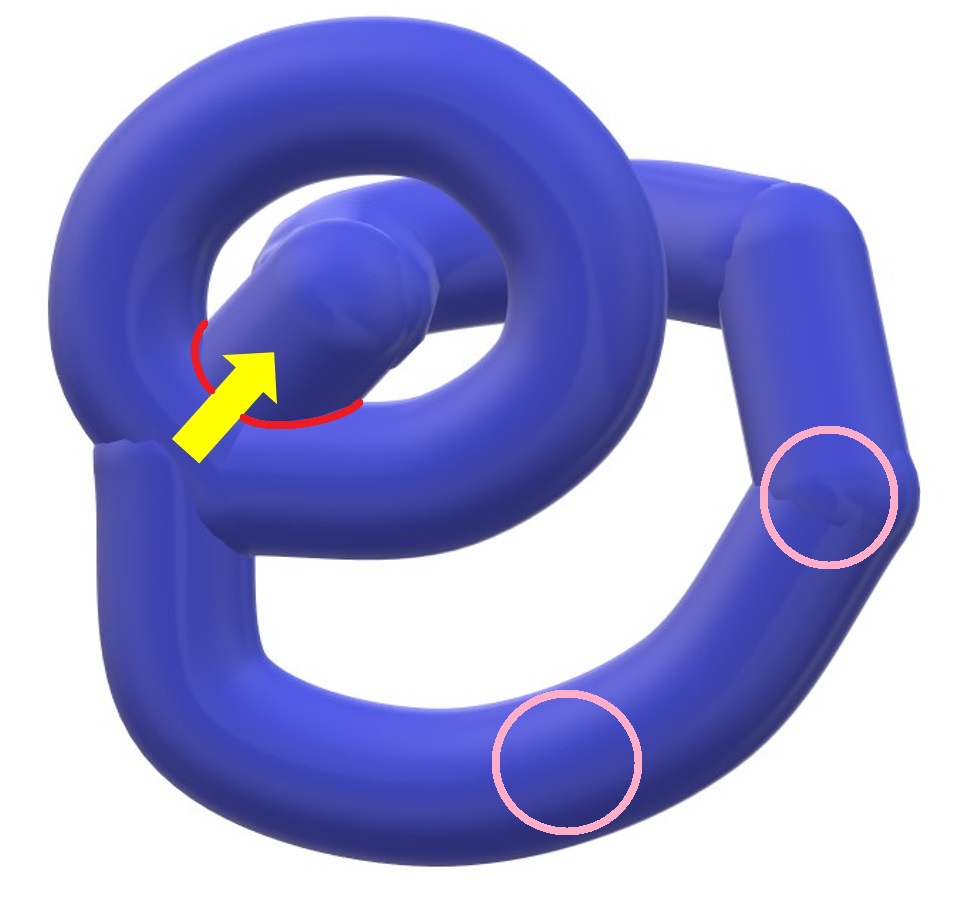
④輪の中をくぐらせた後は付け根を、裏側を通して元の位置に戻していきます。
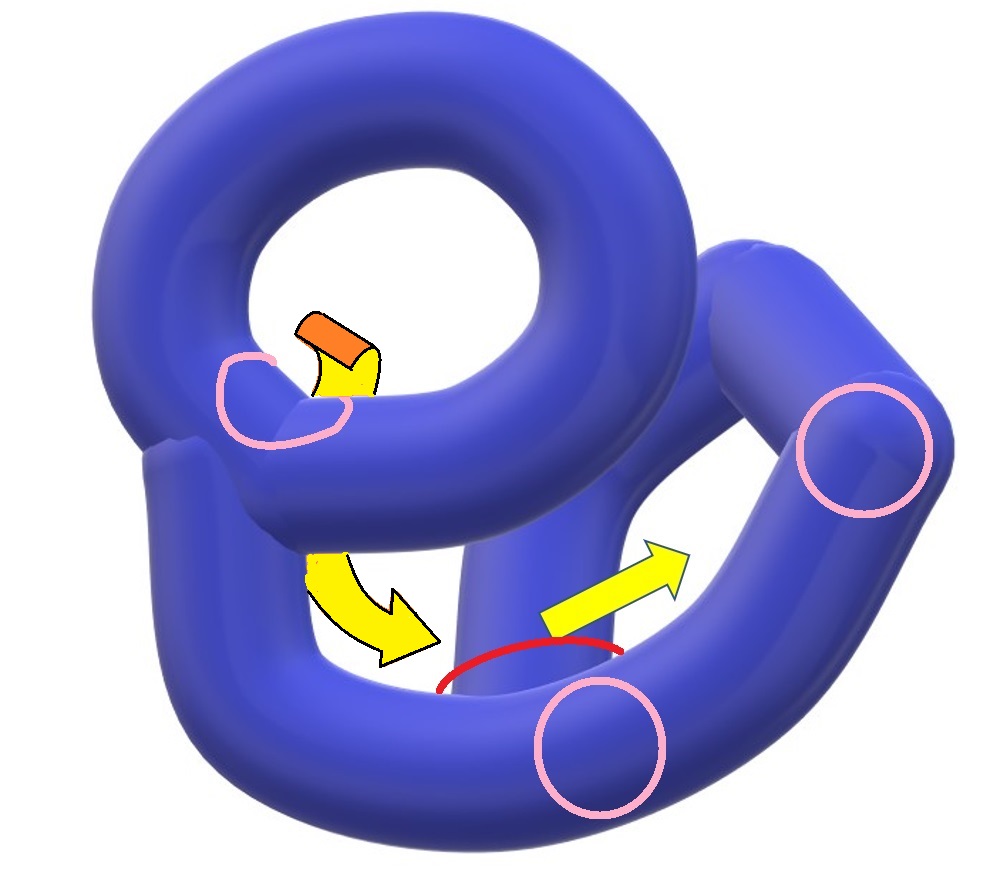
⑤すると、輪が完全にほどけています!

いかがでしたでしょうか。まぎれもなく「切り貼りなし」で絡まりをほどくことができました。しかし、まだまだ分かりにくいと感じる方も多いのではないでしょうか。
難しいのであれば、単純にすればいい!この考え方のもと、上の図形を下の図のように「極限まで単純化」してあげます。
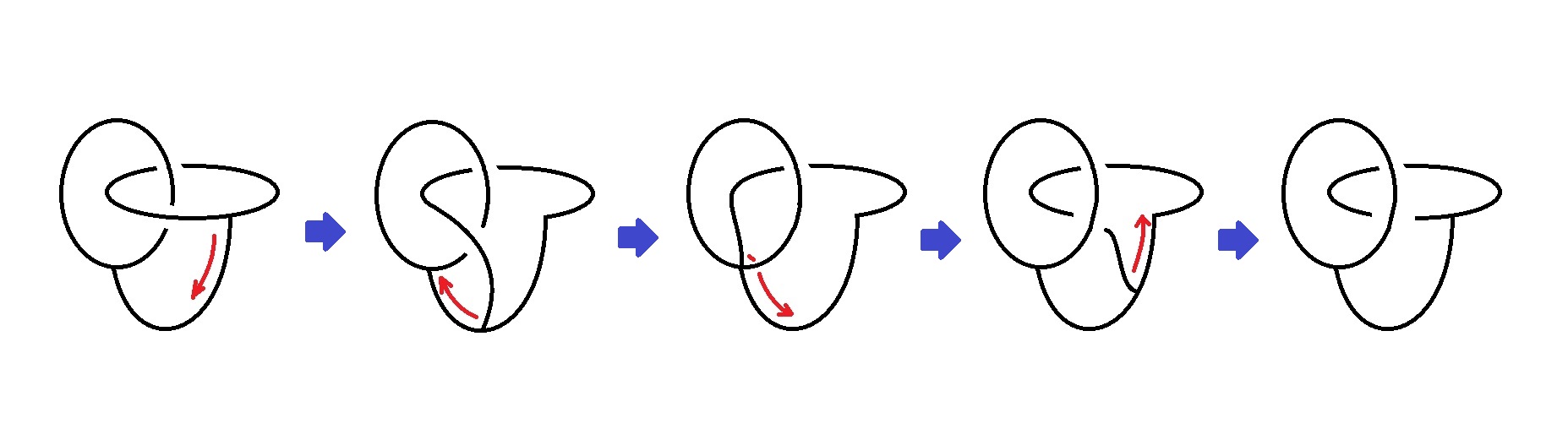
いかがでしょうか?先ほどの立体的な図と比べて、比較的とらえやすくなったのではないでしょうか。想像することには限界があります。そんなときは「骨格にあたる部分」を見極めることで、本質的な問題がわかってきます。
こういったトポロジーの考え方は中学校や高校の授業では登場せず、大学の数学専攻のクラスでないと、なかなか触れ合う機会はありません。最近ではデータ分析の世界でも、トポロジーを応用したトポロジカルデータ分析といった分野が注目されており、ますます発展してきています。
対象物が複雑な構造のように見えても、その骨格や特徴(不変的なもの)をとらえることで、物事の本質的な部分をとらえることができます。こういったトポロジーの考え方は数学だけでなく多くの分野に応用できるのではないかと思っています。
また、イメージが楽しいことからアートやデザインの世界でも登場します。数学とアートに関する無料セミナーもありますので、是非ご参加ください!(数学アート超入門-美しさの中の隠れた数学-https://wakara.co.jp/course/7803)
<文/岡本健太郎>
⇒ 講師紹介ページへ













