はじめに

大人のための数学教室和(なごみ)の講師の松中です。最近印象に残った授業シリーズとして不定期に授業の内容を紹介していきたいと思います。今回紹介したいのは三角関数の合成に関してです。

柔よく剛を制すは数学でも同じ

柔道の世界には「柔よく剛を制す」という言葉がありますが、これは数学においても当てはまる言葉だと思います。高校数学の教科書には公式や問題を解くときの定石が載っていますが、それをそのまま覚えて使おうとすると、問題がいっそう難しそうに見えたり、面白みを感じなかったりします。

公式や定石も大事ですが、それよりも「どんな問題を解きたくて、この概念が出てきたのか」、「何が出発点で、どんな流れで公式が出てくるのか」といった考え方の方がより大事だと考えます。こうした考え方を暗記ではなく、実感として身につけておけば、公式は必要に応じて自分で作れますし、ガチガチに定石を覚える必要もないため、数学の問題にも気楽に立ち向かうことができます。

三角関数の合成の公式

先日高校数学の「三角関数の合成」を授業する機会がありました。お客様のテキストに三角関数の合成の公式「$a\sin{x}+b\cos{x}=\sqrt{a^2+b^2}\sin{(x+\alpha)}$」が書いてあったのですが、私はこれをすごくガチガチな公式であり、押し付けられている感があると感じました。その理由は後述するとして、この公式を使うと、例えば$\sin{x}+\sqrt{3}\cos{x}$は以下のように合成できます。

$$\sin{x}+\sqrt{3}\cos{x}=2\sin{\left(x+\frac{\pi}{3}\right)}$$

$\sin$、$\cos$の関数の和が改めて1つの$\sin$の関数で書けるというのは驚きです。以下のようにグラフを描けば、$\sin{x}+\sqrt{3}\cos{x}$と$2\sin{(x+\frac{\pi}{3})}$が一致することが確認できます。

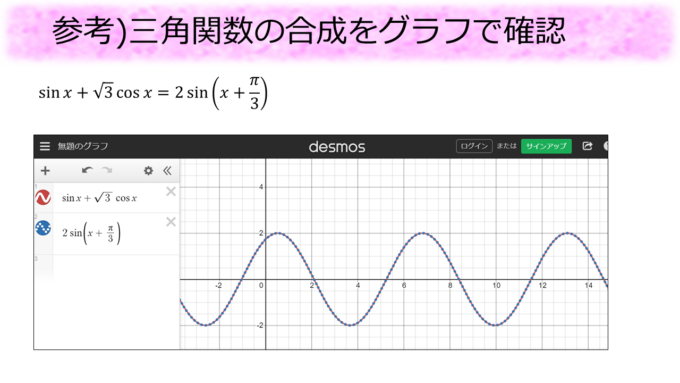
公式をガチガチと感じた理由

三角関数の合成の肝は三角関数の加法定理です。例えば、先ほど例として挙げた三角関数の合成には、

$$\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$$
という$\sin$の加法定理を使っています。

実際、

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\sin{x}\cdot\frac{1}{2}+\cos{x}\cdot\frac{\sqrt{3}}{2}\right)\\=2\left(\sin{x}\cos{\frac{\pi}{3}}+\cos{x}\sin{\frac{\pi}{3}}\right)=2\sin{\left(x+\frac{\pi}{3}\right)}$$

のように加法定理を使って1つの$\sin$にまとめられていたのです。

私がテキストに載っていた三角関数の合成の公式をガチガチと感じた理由は合成に使う加法定理を強制している点です。三角関数の加法定理は次の4つをセットで学ぶことが一般的だと思いますが、

$$\mbox{①}\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}\\ \mbox{②}\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\\ \mbox{③}\cos{(\alpha+\beta)}=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}\\ \mbox{④}\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}$$
この公式では先述した①の加法定理を強制したものになっているのです。このように強制されてしまうと、三角関数の合成は必ずこの公式に従って行わないといけないという強迫観念を与えてしまい、数学の自由さを感じることができずに、数学が苦手になってしまうこともあるかと思います。

ということで、好きな加法定理で合成してみましょう。

好きな加法定理で合成

数学の式変形は間違った変形を行わなければ何をしても自由です。回り道等あったとしても好きにやったらよいです。誰も咎めることはできません。

$\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}$を使う

まずは②の$\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}$を使ってみましょう。第2項の前にマイナスがあることから、以下のように無理やり変形してこの右辺の形に合わせます。

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\sin{x}\cdot\frac{1}{2}-\cos{x}\cdot\left(-\frac{\sqrt{3}}{2}\right)\right)$$

公式と見比べて、$\cos{\beta}=\frac{1}{2}$、$\sin{\beta}=-\frac{\sqrt{3}}{2}$となる$\beta$を探せば、$\beta=\frac{5\pi}{3}$となります。

よって最終的に以下のように合成できます。

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\sin{x}\cdot\frac{1}{2}-\cos{x}\cdot\left(-\frac{\sqrt{3}}{2}\right)\right) \\=2\left(\sin{x}\cos{\frac{5\pi}{3}}-\cos{x}\sin{\frac{5\pi}{3}}\right)=2\sin{\left(x-\frac{5\pi}{3}\right)}$$

$\cos{(\alpha+\beta)}=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}$を使う

次に③の$\cos{(\alpha+\beta)}=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}$を使います。第1項に$\cos$が、第2項に$\sin$が固まっていることから、まず項の順番を入れ替えつつ$2$でくくります。間にマイナスがあることから、以下のように無理やり変形します。

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\cos{x}\cdot\frac{\sqrt{3}}{2}-\sin{x}\cdot\left(-\frac{1}{2}\right)\right)$$

公式と見比べて、$\cos{\beta}=\frac{\sqrt{3}}{2}$、$\sin{\beta}=-\frac{1}{2}$となる$\beta$を探せば、$\beta=\frac{11\pi}{6}$となります。

よって最終的に以下のように合成できます。

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\cos{x}\cdot\frac{\sqrt{3}}{2}-\sin{x}\cdot\left(-\frac{1}{2}\right)\right) \\=2\left(\cos{x}\cos{\frac{11\pi}{6}}-\sin{x}\sin{\frac{11\pi}{6}}\right)=2\cos{\left(x+\frac{11\pi}{6}\right)}$$

$\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}$を使う

最後に④の$\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}$を使います。これはほとんど③と同じなので、一気に式変形します。

$$\sin{x}+\sqrt{3}\cos{x}=2\left(\cos{x}\cdot\frac{\sqrt{3}}{2}+\sin{x}\cdot\frac{1}{2}\right) \\=2\left(\cos{x}\cos{\frac{\pi}{6}}+\sin{x}\sin{\frac{\pi}{6}}\right)=2\cos{\left(x-\frac{\pi}{6}\right)}$$

以上②～④の加法定理を用いても$\sin{x}+\sqrt{3}\cos{x}$の合成ができました。加法定理に当てはめるために無理やりマイナスを作り出す、項の順番を入れ替えるといった操作もしましたが、数学的に間違っていなければ何をしても自由です。加法定理に当てはめるという考え方を知っていれば好きなように合成してもよいのです。ガチガチな公式を与えられてその通りに合成しないといけないと考えていた方には、好きな加法定理を使って自由に合成してもよいよと伝えたいです。

しかし懸念が1つあります。合成の結果出てきた関数がいずれも異なる形をしています。最後にこれらが同じ関数であることは以下のように確認できます。

もちろんグラフを書いても一致していることがわかります。

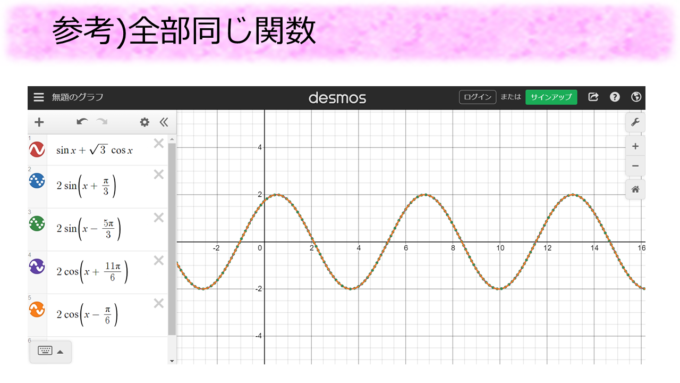
まとめ

今回は最近印象に残った授業ということで三角関数の合成の公式を紹介しました。高校数学の授業をしていると、今回の例のように暗に押し付けられていると感じることが多々ありました。数学は自由なので数学的に正しい範囲で好きに式変形していきましょう!

三角関数を学んでみたい方には以下の講座がおすすめです。

三角関数

(文/松中)