反比例とは【算数からやさしく解説】

算数・物理・数学トピック

公開日

2022年4月14日

更新日

2024年8月4日

↓↓↓動画で見たい方はこちら↓↓↓

この記事の主な内容

反比例とは

反比例とは、一方2倍,3倍,…されるともう一方が\(\frac{1}{2}倍,\frac{1}{3}倍,…\)されるような関係のことです。
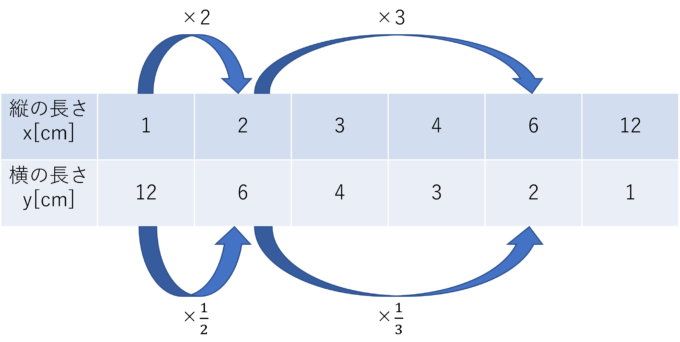
例えば、面積が12\([cm^2]\)の四角形の縦と横の関係は反比例になっています。
縦の長さが1\([cm]\)で横の長さが12\([cm]\)の四角形は面積が12\([cm^2]\)になります。
ここで縦の長さを2倍にして2\([cm]\)として考えると面積は12\([cm^2]\)なので横の長さは6\([cm]\)になり\(\frac{1}{2}\)倍になっているので反比例の関係だとわかります。

反比例の式

先ほどの例から反比例の式を考えてみます。
面積がa\([cm^2]\)の四角形の縦の長さをx\([cm]\)、横の長さをy\([cm]\)とすると四角形の面積の公式から
\begin{align*}
xy=a
\end{align*}
という式が成り立ちます。

この式が常に成り立つためにはxが2倍,3倍,…されるとつじつまを合わせるようにyが\(\frac{1}{2}倍,\frac{1}{2}倍,…\)されないといけないので反比例の関係になっています。
また、xが0になるとどんなyをかけても0以外にはならないのでx,yは0ではありません。

数学ではy=の形で書く方がわかりやすいのでxで両辺を割った
\begin{align*}
y=\frac{a}{x}
\end{align*}
が反比例の式と呼ばれ、aのことを比例定数といいます。

反比例のグラフ

次は反比例のグラフについて説明していきたいと思います。
数学では\(y=\frac{a}{x}\)のような式（関数）を横軸（x軸）と縦軸（y軸）を書いた座標平面に、その関数の式が成り立つような点を打つことで図形として表示したものをグラフと言います。
（実は数学にはいくつかの点とそれらを結ぶ線分のことなど、別の意味でグラフと呼ばれるものもあります。）
例えば、\(y=\frac{12}{x}は(x,y)=(\frac{1}{2},24)(1,12)(3,4)(4,3)\)など無数の点を座標平面に打つことができます。この無数の点をすべてつなげたものがグラフであり、特に\(y=\frac{12}{x}\)は反比例の式だったのでこのグラフを反比例のグラフと呼んだりします。

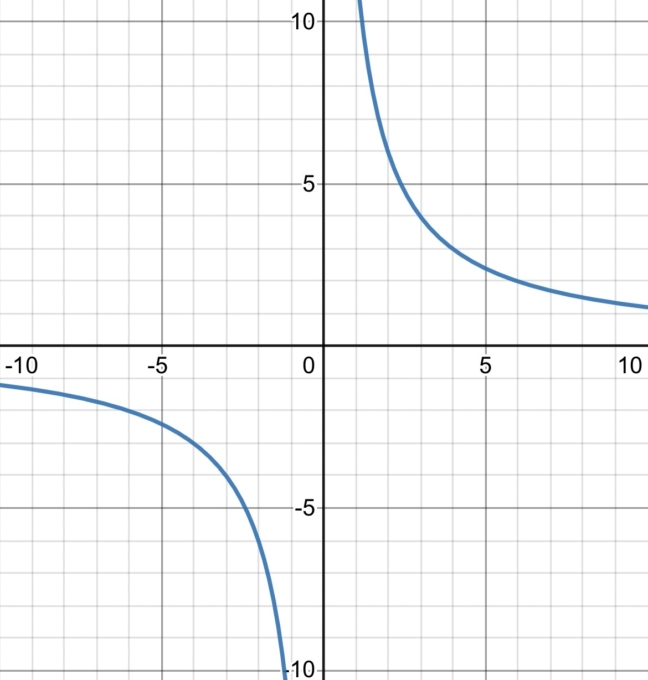
このグラフを見て分かるように、反比例のグラフは右上と左下の2つの曲線でできているので双曲線ともよばれます。
また、今回は比例定数が正の数だったので右上と左下に曲線ができましたが、比例定数が負の数だと左上と右下に曲線ができます。

反比例のメリット

反比例はxに0を代入した値が存在しません、このようにグラフを書いたときにグラフが途切れているような関数を不連続関数、比例の式のようにグラフを書いたときにグラフが途切れていない関数を連続関数といいます。
小中高で扱う関数のほとんどが連続関数であり、反比例のような不連続な関数に触れる機会は少ないです。