原因と結果の思考法-相関の便利さと怖さ
公開日
2020年6月8日
更新日
2020年6月8日

皆さんこんにちは。WAKARAの数学&統計講師の川原祐哉です。
最近は日夜ニュースなどでも「統計」という言葉をよく目にすることと思いますが、統計学はデータを客観的に把握するためのとても便利なツールですね。その統計学を勉強しているとあるところで次の言葉が出てきます。
「相関」
統計学の中でよく使われるこの「相関」ですが、意外としっかりと意味を理解できている人が少ないため、今日はその相関の便利さと怖さを少しお話してみたいと思います。
この記事の主な内容
相関とは
「相関とはデータ間の直線的な関係のこと」です
と、これだけ言っても意味が分からないですよね。なので、少し具体的な例を用いて考えてみましょう。
皆さんコンビニにはよく行きますか?私は毎日といっていいほどコンビニに行くのですが、そこでよく買うものがアイスクリームです。1年を通してアイスクリームをよく買うのですが、家計簿を見てみると、アイスクリームをよく買っている月と、よく買っていない月があることに気づきました。どんな月によくアイスクリームを買っているのだろうと不思議に思った私は、月ごとにアイスクリームを買った回数をデータで取ってみることにしました。それが次の表です。
| 月 | アイスの購入回数 |
|---|---|
| 1月 | 3回 |
| 2月 | 2回 |
| 3月 | 4回 |
| 4月 | 6回 |
| 5月 | 10回 |
| 6月 | 9回 |
| 7月 | 15回 |
| 8月 | 21回 |
| 9月 | 18回 |
| 10月 | 11回 |
| 11月 | 6回 |
| 12月 | 1回 |
この表から何がわかるでしょうか?
真冬でもそこそこアイスを食べていることが見て取れます。他にもよくよくこの表を見てみると、アイスを多く買っている月と、あまり買っていない月が見て取れますね。私はどんな月に多くアイスを買っているのでしょうか…?
その視点でデータを見てみると、7月、8月、9月あたりが多く、12月、1月、2月あたりが少ないことが見て取れます。これから一つこんな仮説が浮かんでくるわけです。「川原は暑くなるとアイスをよく買い、寒くなるとアイスを買わなくなるんじゃないか」よくよく考えれば当たり前だろ、と言われるような例かもしれませんが、大真面目にデータを用いて検証してみましょう。先ほどのデータに、各月の平均気温のデータを追加したものが下の表です。
| 月 | アイスの購入回数 | 平均気温(東京) |
|---|---|---|
| 1月 | 3回 | 5.6℃ |
| 2月 | 2回 | 7.2℃ |
| 3月 | 4回 | 10.6℃ |
| 4月 | 6回 | 13.6℃ |
| 5月 | 10回 | 20.0℃ |
| 6月 | 9回 | 21.8℃ |
| 7月 | 15回 | 24.1℃ |
| 8月 | 21回 | 28.4℃ |
| 9月 | 18回 | 25.1℃ |
| 10月 | 11回 | 19.4℃ |
| 11月 | 6回 | 13.1℃ |
| 12月 | 1回 | 8.5℃ |
さて先ほどのデータに東京の平均気温を追加してみましたが、この表だけでは数字が羅列されているばかりで、なかなか関係性が見えてこないですね。そこで、このデータをグラフで表現してみようと思います。今回使うグラフは散布図というグラフです。
その散布図が下のグラフです。
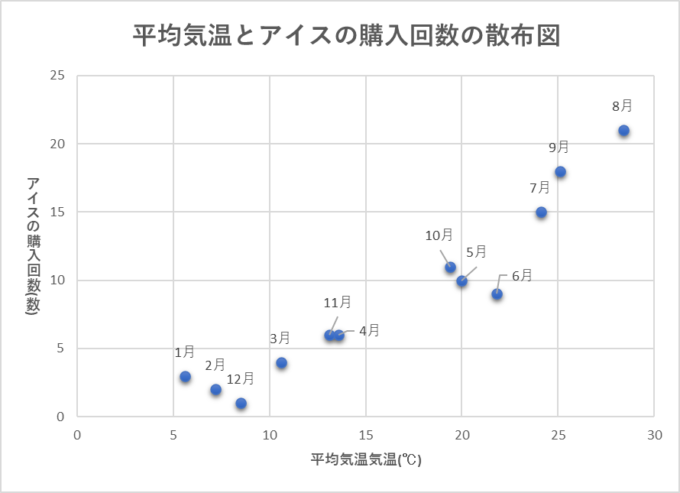
散布図とは2つのデータ(平均気温とアイスの購入回数)を一つの点で表したグラフとなります。このグラフを見てみると点の並び方に少し特徴が見えてきます。その特徴とは点が右上がりの直線形に配置されているということです。
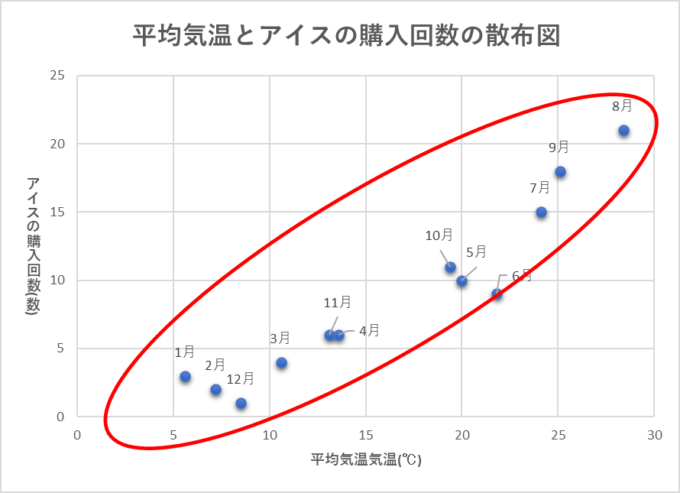
これは何を表すかというと、気温が高い月はアイスの購入回数が多く、気温が低い月はアイスの購入回数が少ないということを表しています。このように、散布図を描いたときに点が直線形に並ぶとき、2つのデータには相関があると言います。
この相関があるデータとは何を表しているかと言えば、それは2つのデータが連動しているということを表しています。今回の例でいうと「東京の平均気温」と「川原のアイスの購入回数」は連動しており、気温が高い月はアイスの購入回数が多い傾向にあるということがいえそうです。このように散布図を使うと2つのデータの関連性を可視化することができてとても便利です。
相関の怖さ
散布図を使えば相関関係を見ることができると先ほどお話ししましたが、ここで一つ注意しなければならないことがあります。それは「相関関係」と「因果関係」は全くの別物だということです。相関関係とは2つのデータに関連性があるといっているだけで、「○○したから●●になった」という因果関係を表していないということになります。先ほどの例で言うならば、気温とアイスの購入回数の間には相関はあると言えますが、気温が高くなったから、アイスの購入回数が増えたというように因果関係までを結論付けることはできません。これはなぜでしょうか?暑くなったからアイスの購入回数が増えたんだろ!と言いたくなりますが、実は世の中には因果関係がないのに相関関係が出てしまう例がいくつか知られているのです。
そのうち今日は全くの偶然で相関関係が出てしまう例があるということを紹介いたします。次の散布図を見てみてください。
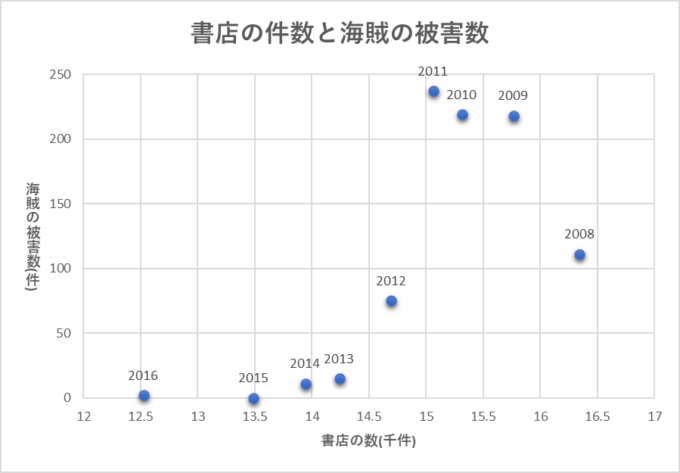
この散布図は日本にある「書店の件数」と「ソマリア沖で起きた海賊被害の件数」を散布図にしたものです。この散布図を見るとどうでしょうか?点が右上がりに配置されていて相関関係が見て取れます。書店の数が多い年は海賊の被害件数も多く、書店の数が少ない年には海賊の被害件数も少ない傾向にあることが見て取れます。これはどんな関係があるのでしょうか?
書店の数が多くなると、海賊活動が活発になるのでしょうか?
または、
海賊活動が活発になると書店の数も増えていくのでしょうか?
はい、皆さんお気づきだと思いますが、これは全くの偶然です。現代社会には数多くのデータがあり、そのたくさんあるデータの中から適当なものを選び出すと偶然にも相関関係が出てしまうような例がたくさん存在してしまうんです。この偶然の相関関係を因果関係だと勘違いしてしまうとても怖いことになります。
この例から相関関係が出たからと言って因果関係があるとまで言うことができないということがお分かりいただけたかと思います。
まとめ
今回相関関係という言うものについて簡単に解説してきました。次回は因果関係とは何かということについてお話させていただく予定ですのでお楽しみに。
また弊社和から株式会社では、この相関関係と因果関係の違いや、因果関係を正しく図るためにはどうしたらよいか、ということを題材に初心者向けのセミナーを無料で行っております。因果、相関をこれから学んでみたいという方、今回の記事で因果推論について興味を持たれた方はぜひ参加いただけたら嬉しく思います。
(文/川原祐哉)












