確率分布とは

確率分布とは、確率変数の値と確率の対応のことです。確率分布を理解するためにはまず確率変数の考え方を理解する必要があります。

確率・統計の分野では、事象に対して確率変数という数を割り当てます。具体的には、「勝ち」を\(1\)・「負け」を\(0\)としたり、「サイコロを振って\(1\)の目が出る」という事象を\(1\)に割り当てるような対応を考えます。確率が分かっている事象に対して、\(1\)や\(0\)などの確率変数を対応させることによって、数学を用いて統計学を考えることができます。確率変数は通常\(X,Y,Z\)などの大文字のアルファベットで表されます。

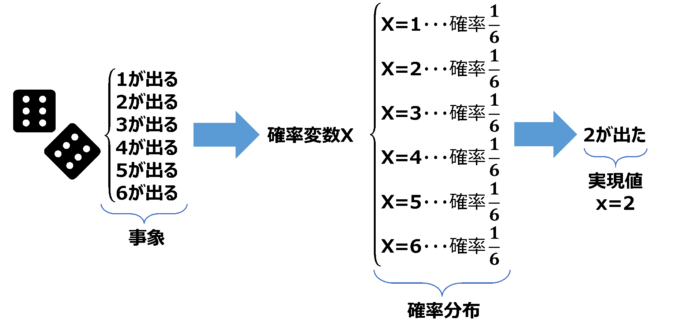
例えば、サイコロの出る目を表す確率変数\(X\)を考えてみます。{\(1\)が出る, \(2\)が出る, \(3\)が出る, \(4\)が出る, \(5\)が出る, \(6\)が出る}という事象の組に対して、確率変数では\(X=\){\(1,2,3,4,5,6\)}という数が割り当てられます。この確率変数\(X\)のそれぞれの値に対して確率\(\frac{1}{6}\)を対応させた関係のことを確率分布といいます。また、実際にサイコロを振ったときに出た目の数のことを実現値とよび、通常\(x,y,z\)などの小文字のアルファベットで表されます。

この例を図にすると、以下のような関係になります。事象に対して割り当てられた数を確率変数と呼び、確率変数と確率の関係を表したものが確率分布です。最後に、実際にサイコロを振って出た目が実現値になります。

確率密度関数とは

確率変数に対して確率を対応させる関数を確率密度関数と呼びます。確率変数の値を確率密度関数に入れると、その確率変数に対応する確率が計算されます。確率変数\(X\)が実現値\(x\)を取る確率は\(f_X(x) \)と表され、\(x\)の関数です。サイコロの例であれば、確率は確率変数の値に依らず、全て\(\frac{1}{6}\)になるため、確率密度関数は\(f_X(x)=\frac{1}{6}　(X=1,2,3,4,5,6) \)となります。

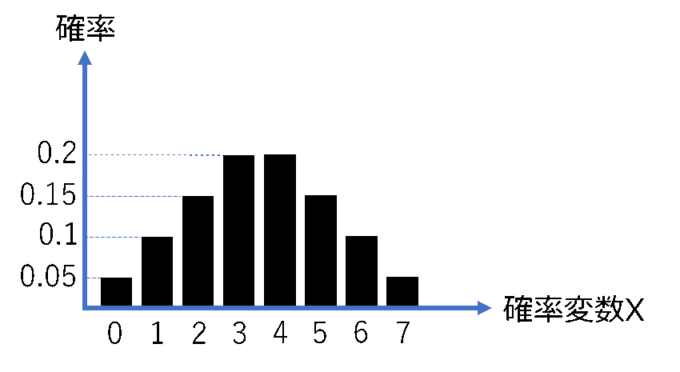
下の図では、ある確率分布の確率密度関数を表しています。
確率変数\(X\)の取りゆるそれぞれの値に対して確率が、
\(f_X(x)=0.225-0.05|x-3.5|\) 　\((X=0,1,2,3,4,5,6,7) \)という風に分布しています。
実際に、\(X=0\)となる確率は
\(f_X(0)=0.225-0.05|-3.5|=0.225-0.05×3.5=0.05\)
となり、グラフ上の確率と一致します。このように、確率密度関数に確率変数の値を入れることによって確率を計算することができます。

確率密度関数には、満たさなければならない性質があります。
はじめに、確率密度関数は確率を表すため、その和は\(１\)である必要があります。
同じ理由から、確率は負の値を取らないことから、確率密度関数の値は必ず\(0\)以上です。

累積分布関数とは

累積分布関数とは確率変数がある値以下を取る確率を示す関数です。具体的には、確率変数\(X\)がある値\(x\)を下回る確率は\(F_X(x) \)と表され、\(x\)の関数になります。

累積分布関数の考え方は度数分布表の累積相対度数の考え方で理解することができます。度数分布表では、データを分類する階級に対して、データの個数を表す度数が示されます。また、総データ数に対しての度数の割合を相対度数と呼び、最も小さい度数からその階級までの相対度数を足し合わせたものが累積相対度数です。
確率分布では、階級が確率変数に対応し、相対度数が確率密度関数に対応します。確率密度関数をある値まで足し合わせた関数が累積分布関数なので、累積相対度数は累積分布関数に対応します。確率密度関数では、ある一点の確率を知ることができる一方、累積分布関数はある一点までの確率の和を知ることができます。上のグラフの例では、累積分布関数の値は\(X=0\)で\(0.05\),　\( X=1\)で\(0.15\),　\( X=2\)で\(0.3\)…となります。

累積分布関数を用いることで確率変数がある範囲を取りゆる確率を求めることができるため、便利です。\(F_X(b)-F_X(a) \)を計算することによって、\(X\)が\(a\)より大きく、\(b\)以下である確率を求めることができます。

まとめ

この記事では、確率変数と確率の関係である確率密度関数と累積分布関数について解説しました。確率分布には、確率変数\(X\)が整数値である離散型と\(Ｘ\)が連続値である連続型が存在します。今回の記事では、離散型の確率密度関数を用いて解説しています。連続型の確率密度関数や累積分布関数では、解釈が異なる点があり扱いが難しくなります。

●和からのセミナー一覧はこちら

●お問い合わせフォームはこちら

<文/須藤>