感銘を受けた数学「世界をつなぐ夢幻の等式」

ロマンティック

公開日

2020年8月13日

更新日

2020年8月13日

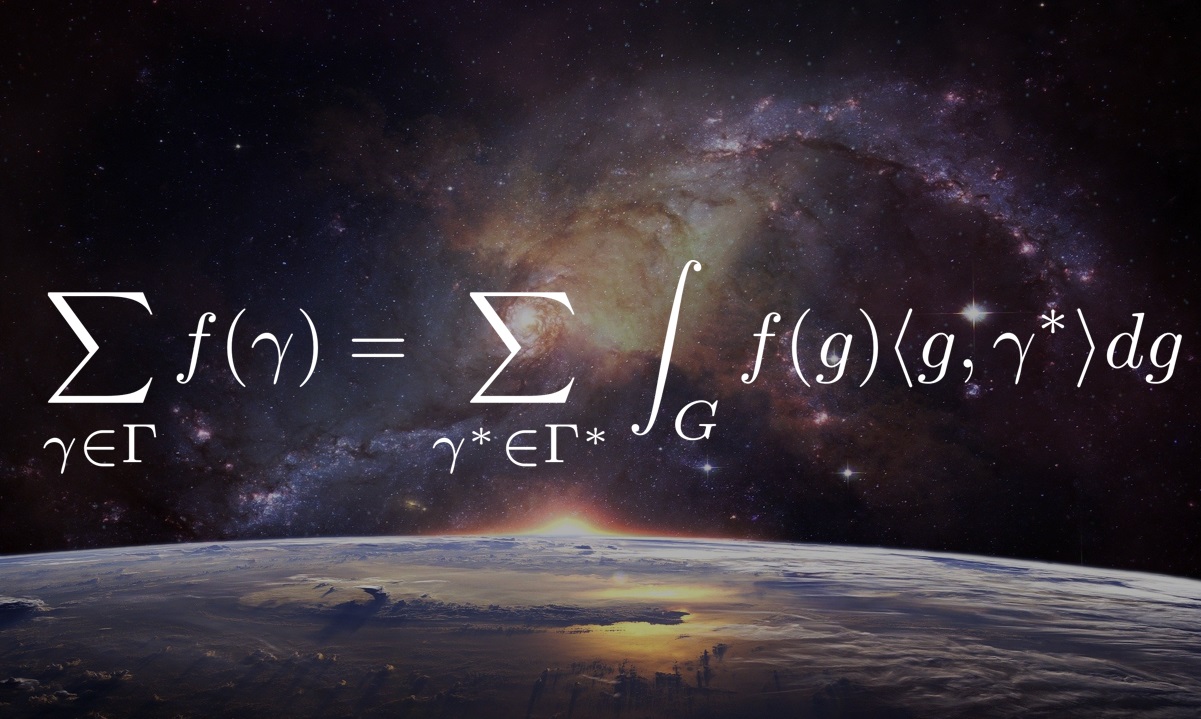
こんにちは。和からの数学講師の岡本です。おなじみになってきました、岡本の「感銘を受けた数学シリーズ」、本日は第４弾です。今日は魅力的な等式“ポアソン和公式”についてお話をいたします（かなりマニアックですのでご注意ください）。

このポアソン和公式は個人的に最も好きな等式で、どれだけ好きかというと、自分の名刺に載せてしまうほど好きです。

この記事の主な内容

１．出会いはゼータ。

突然ですが、みなさんは「ゼータ関数」ってご存じですか？実はたくさんの「ゼータ関数」というものが存在しているのですが、ここではそれらの“始祖”ともいえる「リーマン・ゼータ関数」についてお話します。

リーマン・ゼータ関数とは、天才数学者ベルンハルト・リーマンによってはじめて定義された以下のような複素関数です。

\begin{align*}\zeta(s):=\sum_{n=1}^{\infty}\frac{1}{n^s}\hspace{1.0cm}(\mathrm{Re}(s)>1)\end{align*}

この関数で有名なのが未解決問題である「リーマン予想」で、「\(\zeta(s)=0\)となる複素数\(s\)は負の偶数と直線\(\mathrm{Re}(s)=1/2\)上にあるものが全てだろう」というものです。これは人類の存亡がかかっているというと大げさですが、それぐらい重要な未解決問題です。何せ、１億円の賞金首です。詳しくは以前のマスログで解説していますので、興味のある方はご覧ください。

ミレニアム懸賞金問題―リーマン予想前編―

ミレニアム懸賞金問題―リーマン予想後編―

さまざまな研究がなされているリーマン・ゼータ関数の著しい性質の一つに「関数等式」というものがあります。ガンマ関数といわれる特殊な関数\(\Gamma(s)\)と円周率\(\pi\)を用いて以下のような等式が成り立ちます。

\begin{align*}\pi^{-s/2}\Gamma(s/2)\zeta(s)=\pi^{-(1-s)/2}\Gamma((1-s)/2)\zeta(1-s).\end{align*}

つまり、複素数「\(s\)」と「\(1-s\)」の間で、ある種の対称性があることを主張する大変美しい等式です。この等式も十分魅力的なのですが、なぜこの等式が成り立つかという「ルーツ」をたどっていくと、そこには「ポアソン和公式」があるのです。

２．世界をつなぐポアソン和公式

前節ではリーマン・ゼータ関数の関数等式のルーツとして「ポアソン和公式」があることを述べました。いわば、関数等式の美しさのカギを握る存在です。

キーワードは「フーリエ変換」。フーリエ変換とは、実数\(\mathbb{R}\)上の「良い性質」の関数\(f(x)\)に対して以下のような積分を使った変換のことを言います。

\begin{align*}\widehat{f}(y):=\int_{-\infty}^{\infty}f(x)e^{-2\pi ixy}dx\end{align*}

数学、物理、工学のあらゆるところで登場し、さまざまな応用が存在する超重要な変換です。

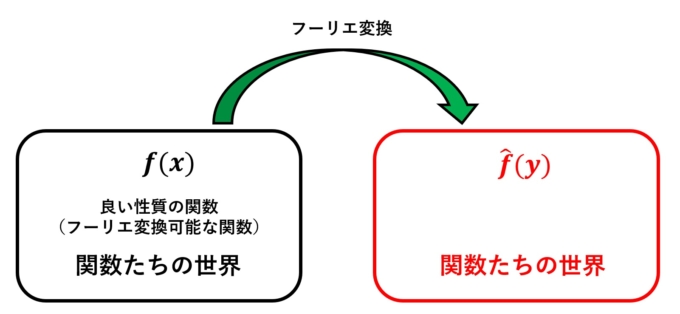
さて、関数をフーリエ変換することで新たな関数が出来上がります。例えば関数として\(f(x)=e^{-2\pi|x|}\)をフーリエ変換すると

\begin{align*}\widehat{f}(y)&=\int_{-\infty}^{\infty}e^{-2\pi |x|}e^{-2\pi i xy}dx\\ &=\int_{-\infty}^{0}e^{2\pi (x-ixy)}dx+\int_{0}^{\infty}e^{2\pi(-x-ixy)}dx \\ &=\frac{1}{2\pi(1-iy)}+\frac{1}{2\pi(1+iy)}\\ &=\frac{1}{\pi(1+y^2)}\end{align*}

となり、元の関数とは別物の新しい関数が出来上がりました。実は、「大変良い性質」の関数におけるフーリエ変換前後に対し、次のような驚くべき等式が成り立ちます！

\begin{align*}\sum_{n\in \mathbb{Z}}f(n)=\sum_{m\in \mathbb{Z}}\widehat{f}(m)\end{align*}

ここで、和は整数の集合\(\mathbb{Z}\)全体を走ります。つまり書き下すと、

\begin{align*}\cdots+f(-1)+f(0)+f(1)+f(2)+\cdots =\cdots +\widehat{f}(-1)+\widehat{f}(0)+\widehat{f}(1)+\widehat{f}(2)+\cdots \end{align*}

という等式が成り立つというのです！これをポアソン和公式と呼びます。ポアソン和公式はフーリエ変換以前の世界と、後の世界をつなぐ重要な等式です。例えば、さっきの関数\(f(x)=e^{-2\pi|x|}\)に対してポアソン和公式を使うと

\begin{align*}\sum_{n\in \mathbb{Z}}e^{-2\pi n}=\sum_{m\in \mathbb{Z}}\frac{1}{\pi(1+m^2)}\end{align*}

が成り立ちます。これらを整理すると

\begin{align*}\pi\frac{1+e^{-2\pi}}{1-e^{-2\pi}}=\sum_{m\in \mathbb{Z}}\frac{1}{m^2+1}=\frac{1}{1}+\frac{2}{1^2+1}+\frac{2}{2^2+1}+\frac{2}{3^2+1}+\cdots\end{align*}

といった、何やら魅力的な無限和の等式が得られます。なお、リーマン・ゼータ関数の関数等式を証明するときにも、このポアソン和公式を使うのですが、本質的には正規分布の関数で知られる「ガウス関数（ガウシアン）」

\begin{align*}f(x)=e^{-\frac{x^2}{2}}\end{align*}

のフーリエ変換を計算することで証明できます！

ちなみにフーリエ変換は「係数を抽出する」というイメージです。なのでポアソン和公式でフーリエ変換後の関数を全部の整数で足し合わせているのは、「全ての係数を足し合わせる」という感覚です。

３．一般化された世界での再会

さて、このフーリエ変換やポアソン和公式、非常に一般化がなされています。上の例では実数という世界で考えていましたが、「群」と言われる抽象的な世界の中でも考えることができます。演算が交換可能（可換といいます）な群（アーベル群）かつ局所的にコンパクトなハウスドルフ空間であればOKです。このような群を局所コンパクトアーベル群といい、実数\(\mathbb{R}\)も局所コンパクトアーベル群の一種です（以降局所コンパクトアーベル群は\(G\)と表記することにします）。非常に複雑ですが、このような条件があれば、\(G\)上の関数\(f(g)\)に対していわゆる「積分」を行うことができます！そのため、\(G\)上の「良い性質」の関数についてフーリエ変換を以下のように定めることができます。

\begin{align*}\widehat{f}(g^{*}):=\int_{G}f(g)\langle g,g^{*}\rangle dg.\end{align*}

ここで\(\langle g, g^{*}\rangle\)というのは、先に述べたフーリエ変換における\(e^{2\pi i xy}=\langle x,y \rangle\)に対応するものだという認識で構いません。

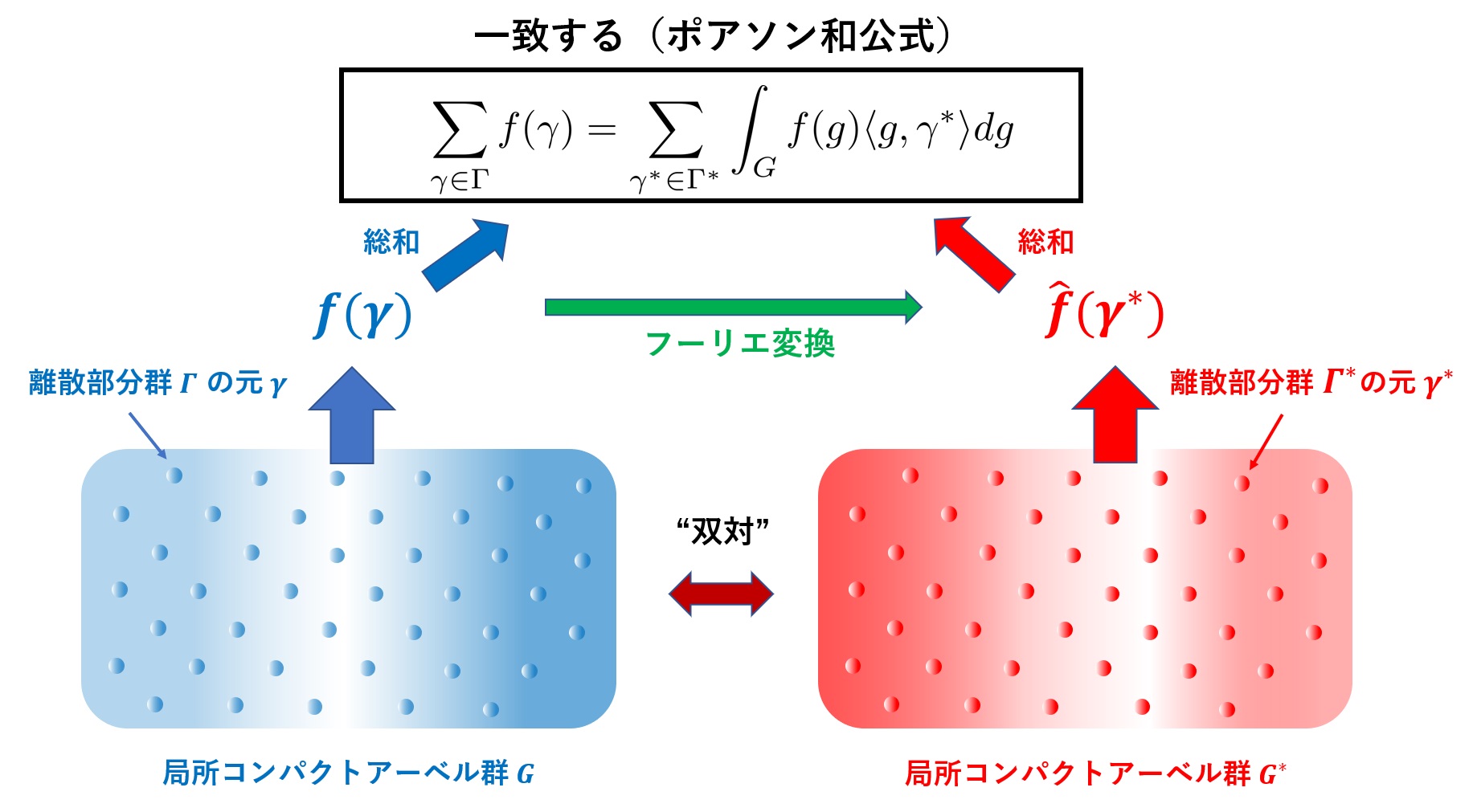
そしてさらにすごいのは、フーリエ変換後の世界\(G^{*}\)（双対群といいます）にも、局所コンパクトアーベル群の構造が入ることが知られています！そして\(G\)上の「大変良い性質」の関数\(f(g)\)と、\(G\)の中の「離散部分群\(\Gamma\)」（実数\(\mathbb{R}\)の部分集合である整数\(\mathbb{Z}\)に対応する「離散的な」集合）のペアについても、以下のようにポアソン和公式を考えることができるのです！

\begin{align*}\sum_{\gamma \in \Gamma}f(\gamma)=\sum_{\gamma^*\in \Gamma^{*}}\widehat{f}(\gamma^{*})=\sum_{\gamma^*\in \Gamma^{*}}\int_{G}f(g)\langle g, \gamma^{*} \rangle dg\end{align*}

これが岡本の愛する等式です。名刺を見ればいつでも会えます。

なお、有理数体（あるいは一般の数体）を完備化した世界である実数体\(\mathbb{R}\)、複素数体\(\mathbb{C}\)、\(p\)進数体\(\mathbb{Q}_p\)（\(p\) は素数あるいは極大イデアル）は全て局所コンパクトアーベル群であることが知られています。さらにこれらを制限直積という操作で得られる巨大な空間“アデール\(\mathbb{A}\)”も局所コンパクトアーベル群となります。それぞれの世界でこの一般化されたポアソン和公式が成り立ち、ゼータ関数やその親戚である\(L\)関数の解析的性質を調べるときに利用されます。奥が深いですね。

４．さらなる高みへ―跡公式―

さて、このポアソン和公式ですが、「跡公式」という視点からより広い世界を見渡すことができます。その最もシンプルな例が行列のトレース（跡）です。線形代数で出てくる「行列」。ベクトル空間からベクトル空間への「線形写像」としてとらえることもできます。ここでは対角化可能（大変良い性質）な\(n\times n\)の行列\(A\)を考えます。対角化とはある正則行列\(P\)を使って行列\(A\)を対角行列という見通しのいい行列に変換することをいいます。

\begin{align*}P^{-1}AP=P^{-1}\left( \begin{array}{ccc} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{n,1}& \cdots & a_{n,n} \end{array} \right)P=\left( \begin{array}{ccc} \lambda_1 & \ & \\ & \ddots & \\ & & \lambda_n \end{array} \right)\end{align*}

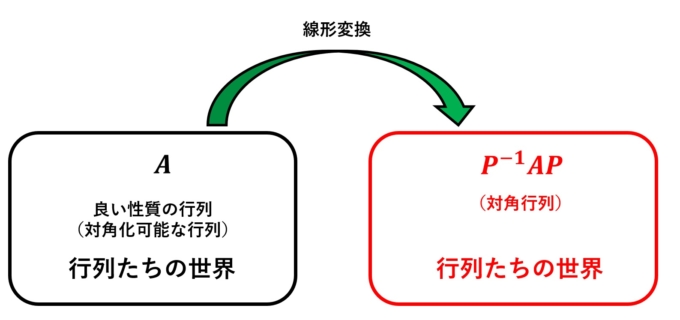
ここで、ポアソン和公式のときに扱った「大変良い性質の関数」を「フーリエ変換」することと、「大変良い性質の行列（線形写像）」を「対角化」することを対応させてみましょう。実はこのとき、行列の対角成分のみを足し合わせる跡（トレース、\(\mathrm{tr}\)）に関して次のような等式が成り立ちます。

\begin{align*}\mathrm{tr}A=a_{1,1}+\cdots+a_{n,n}=\mathrm{tr}(P^{-1}AP)=\lambda_1+\cdots+\lambda_n.\end{align*}

大学初年次に出てくる線形代数の基本的な公式の１つであり、このような有限サイズの行列の対角成分における等式は「跡公式」の単純な例となっています。先ほど述べたフーリエ変換はおおよそ無限次元バージョンだったわけです。

数学の世界では、フーリエ変換、対角化、メリン変換、メビウス反転公式など、「変換（あるいは作用素）」により移った後の世界と移る前の世界をつなぐ魅力的な等式がしばしば現れます。これらは総じて跡公式という視点で統一的に眺めることができ、特に「非可換」の場合（アーベル群でない位相群に関して）大きな進展として有名なのが「セルバーグ跡公式」です。いわば、ポアソン和公式の真の姿といったものです。

実際に大変良い性質の作用素とそれらを結ぶ等式（跡公式）という視点から、セルバーグ・ゼータ関数（ざっくり言うと“幾何学のゼータ関数”）というゼータ関数に関するリーマン予想（の類似物）がセルバーグによって解決されてました。このセルバーグによる仕事がターニングポイントとなり、続けて合同ゼータ関数（ざっくり言うと“代数多様体のゼータ関数”）のリーマン予想（の類似物）もドリーニュにより解決され、本家本元のリーマン・ゼータ関数の解決に向けた方針が徐々に定まってきました。リーマン予想解決も、夢でなくなってきたのです！！

５．さいごに

\begin{align*}\sum_{\gamma \in \Gamma}f(\gamma)=\sum_{\gamma^*\in \Gamma^{*}}\int_{G}f(g)\langle g, \gamma^{*} \rangle dg\end{align*}

いかがでしたでしょうか。ぱっと見意味不明な等式ですが、実は世界を揺るがす大変美しい“夢幻の等式”だったということで今回のお話は終わりにしようと思います。最後にオススメの書籍をご紹介いたします。まずは黒川先生と小山先生の著書「リーマン予想のこれまでとこれから（日本評論社）」。ポアソン和公式からセルバーグ跡公式まで、わかり易くまとめてあり、概観をつかむのに超オススメです。