さて、リーマン予想後編ということで、もう少し詳しくお話をしていこうと思います。
前半を読まれていない方はこちらから↓

ミレニアム懸賞金問題―リーマン予想 前編―

まずは主張についてもう一度見直してみましょう。簡単にいうと、リーマンゼータ関数

$$\zeta(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\cdots$$

が０になる点(ゼロ点)についての予想でした。しかもそのゼロ点は単純なゼロ点(負の偶数点)とそうでないゼロ点(非自明ゼロ点)の２種類に分類されることがわかっています。リーマン予想は、後者のゼロ点に注目します。

Since 1859

リーマン予想が提出されたのは、今から160年前の1859年。未だに解決に至っていません。リーマン自身は、証明はできなかったものの、この予想がもし正しい場合、素数についてどれだけのことがわかるのかということを彼の代表論文「Ueber die Anzahl der Primzahlen unter einer gegebenen Grosse(与えられた数より小さい素数の個数について)」において考察しています。

この論文ではリーマン予想の提示以外にも、

• ・ゼータ関数を「解析接続」という手法を用いて、複素数全平面で定義
• ・ゼータ関数の関数等式の証明(２通り)
• ・「明示公式」

といった内容が含まれています。この中で、素数に関する「明示公式」について次節で詳しく見ていきましょう。

２．リーマンの明示公式

明示公式とは、素数とゼータ関数のゼロ点たちの関係を記述する公式のことで、リーマンの素数公式とも呼ばれています。ここではある数\(x\)よりも小さい素数たちの個数を\(\pi(x)\)と書くことにします。つまり、\(\pi(10)\)と書けば、「\(10\)より小さい素数の個数」を表します。\(10\)より小さい素数は\(2, 3, 5, 7\)の４つなので、

$$\pi(10)=4$$

となります。つまり、この関数 \(\pi(x)\) がわかれば、素数\(p\)について

$$\pi(p)=n-1$$

であるとき、その素数\(p\)は\(n\)番目の素数を表すことになります。また、関数\(y=\pi(x)\)は以下のような階段のような形になり、「素数階段」と呼ばれています。

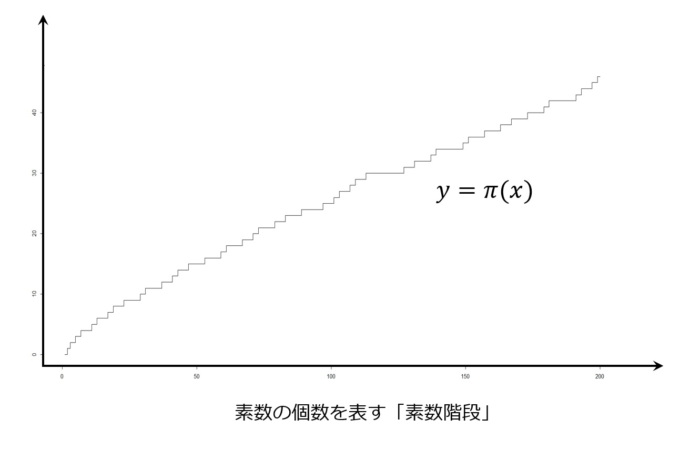
さらに、リーマンの示した「明示公式」を使えば、この関数 \(\pi(x)\)はなんと以下のように具体的に表すことができるのです。

上式の\(\rho\)とは、リーマンゼータ関数の非自明なゼロ点を表します。つまり、非自明ゼロ点たちの規則がとらえられれば、素数の規則をとらえることができるのです！
リーマン予想とは、ゼロ点の分布に関する予想でした。このようなことから、素数の謎を解き明かすためにはリーマン予想解決が重要なカギになるというわけです。

３．リーマン予想解決に向けて

リーマン予想を証明するべく多くの数学者が挑みましたが、いまだに解決されていません(2020年1月現在)。しかし、解決に至ってはいないものの、多くのアイデアが生まれるなど、数学は爆発的に発展してきました。その中でも特に著しい研究の広がりを見せたものの１つに、「ゼータ関数論」があります。リーマンの考えた「リーマンゼータ関数」はリーマン予想のいわば主人公のようなものです。そこで、研究の方針としてゼータ関数について深く考察することが考えられてきました。

$$\large{\zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}}$$

当初、リーマンが定義した複素関数は「自然数の逆\(s\)乗和」というものでしたが、リーマゼータ関数の研究を続けてもなかなかリーマン予想の証明にたどり着けませんでした。
人を観察する場合、１人だけをずっと見ていてもわからないことはたくさんあります。そこで、友人や親戚、会社の同僚など身近な人と比較し、関係性をみることで、その人の本質がわかってくることがあります。たとえば、母親がドイツ人であれば、「娘はドイツ語が話せるのではないか」といった具合に予測でき、見通しが良くなることがあります。

そこで、数学者たちは、リーマンゼータ関数の「兄弟たち」を研究しはじめました。

３.１．ディリクレ級数

数列\(a_1,a_2,a_3,\cdots\)といったものが与えられているとき、これをリーマンゼータ関数の各項に対応させて、次のような無限和を考えます。

このような、数列\(\{a_n\}\)から決まる関数をディリクレ級数と呼びます。数列が常に\(a_n=1\)であれば、ディリクレ級数はリーマンゼータ関数に一致します。つまり、この関数はリーマンゼータ関数の一般化になっています。
さらに、特殊な数列を与えることによってこのディリクレ級数と素数を結びつけることができます。そうなるような数列の条件とは

$$a_1=1\\
a_{n\times m}=a_n\times a_m$$

の２つです。この条件を満たすような数列を完全乗法的であるといいます。
この条件を満たすような数列に関しては次のような性質が言えます。

$$\large{L(s,\{a_n\})=\prod_{p:\mbox{素数}}\frac{1}{1-a_pp^{-s}}}$$

このように、素数との関係を意識しつつ、一般化されたディリクレ級数を考えることで、もともとのリーマンゼータ関数を理解しようという作戦です。

３.２．デデキントゼータ関数(数の世界を一般化したい)

つづいては「数の世界」を一般化するという考えをご紹介します。通常、数や素数の性質などといった数学の研究分野は総じて「整数論」と呼ばれます。この「整数」というものを一般化することを考えます。例えば普段私たちが口にするようないわゆる「整数」というのは、ざっくりいうと実数の中にぽつぽつと存在しています。

　　　　　　　　
では、実数よりも広い、複素数という範囲にぽつぽつと存在するものをうまく見つけてあげて、それも“整数”と呼ぶというアイデアはいかがでしょうか。

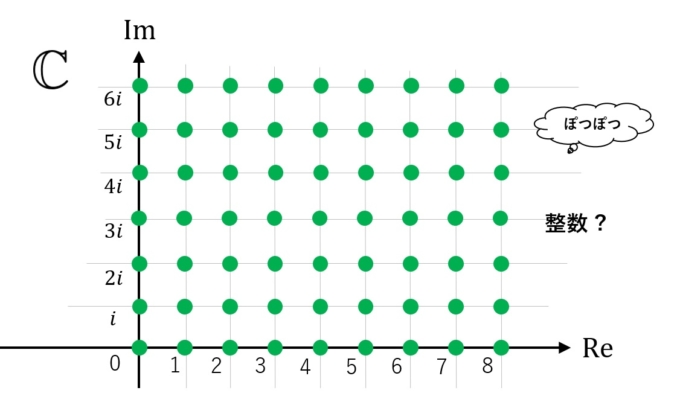
上の図のように、\(a+bi\)(\(a,b\)は整数)という形の複素数をガウス整数といいます。しかもこの世界では、“素数”がもっと細かく分解されます。たとえば、普通の世界の素数とは

$$2,3,5,7,11,13,\cdots$$

でした。しかし、\(5\)という素数はガウス整数の世界だと

$$5=(2+i)\times (2-i)$$

というように、“素因数分解”されてしまいます！
実は「\(4\)で割って\(1\)余る素数」は必ずガウス整数の世界で分解されてしまうということがわかっています。このように数の世界を広げる(数体の有限次Abel拡大を考える)ことで、数の分解されていく法則をとらえる理論というものが知られています。
このように、実はいろいろな世界の中に「整数」という概念があります。リーマンゼータ関数が、正の整数とその世界の素因数分解を象徴するように、一般化された数(これをイデアルといいます)の世界でも同じような関数が考えられるのではないか。こうした流れから生まれたのがデデキントゼータ関数です。

$$\large{\zeta_K(s)=\sum_{{\mathfrak a}}\frac{1}{N({\mathfrak a})^s}}$$

こうした、数の世界のゼータ関数はさらにさまざまな一般化がなされ、研究されていきます。

３.３．歴史的発見

このように、整数論において様々なゼータ関数が考えられ、その特徴が研究されてきました。しかし、リーマン予想の解決に向けた決定的な進展はないままでした。そこで、

• ・無限和の関数
• ・素なものへの分解

といった特徴に注目して、整数の世界に限らず幾何学や解析など、あらゆる数学の分野の中でゼータ関数の「親戚」を考えるようになりました。1950年代に数学者のアトル・セルバーグは、幾何学の研究対象(多様体、リーマン面)に対して定まる“素な閉測地線”というものを、数の世界の“素数”と対応させることで、幾何学のゼータ関数を構成することに成功しました。

$$\large{\zeta_\Gamma(s)=\prod_{{\mathfrak p}:\small{\mbox{素測地線}}}\:\,\,\,\prod_{k=0}^{\infty}(1-N({\mathfrak p})^{-s-k})}$$

さらに、なんとこのセルバーグゼータ関数については、リーマン予想が成立することが証明されました。　

これはすごい発見です。ついに、リーマン予想を満たす親戚が現れたのです！
さて、数学者たちが注目したのは、この「リーマン予想」がなぜ証明できたのかという点です。
※それぞれのゼータ関数における「リーマン予想の類似的な性質」を単純に「リーマン予想」と呼ぶことにします。

まず結論をいうと、セルバーグゼータ関数の背後にある巨大な“作用素”が存在することが、リーマン予想解決の決め手となっています。作用素というのは、「行列」のように、ベクトルを別のベクトルに「変換」させる道具のことです。

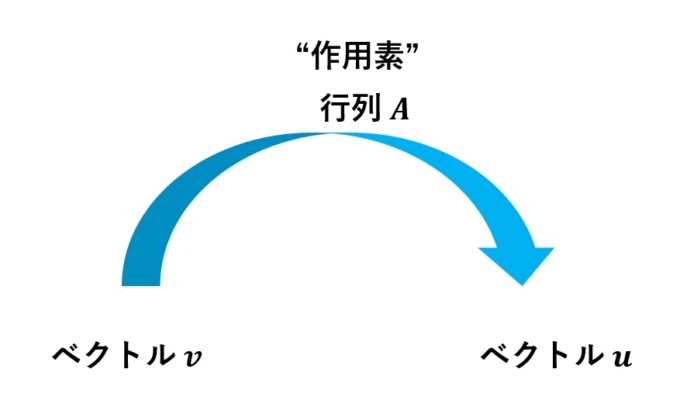
セルバーグゼータ関数のゼロ点は、「ラプラス作用素」との密接な関係があることが証明されています。その作用素の「自己共役」といった性質がわかれば、ゼロ点の規則がわかり、リーマン予想の類似が証明される、といった仕組みになっているのです。

ということで、このような図式が本家のリーマンゼータ関数でも成り立つのではないかと推測されます。つまり、リーマンゼータ関数の背後にもなにか巨大な“自己共役作用素”が存在すれば、リーマン予想が解決されるだろうということです。

４．ヒルベルト・ポリア予想と今後の展開

実はこうした「巨大な自己共役作用素の存在」という考え方は『ヒルベルト・ポリア予想』としてすでに1910年頃に示唆されていましたが、1956年のセルバーグの仕事により、この考えの信憑性が大いに高まりました。
　その後も、ゼータ関数の親戚の１つである「合同ゼータ関数」について、エタール・コホモロジーのフロベニウス作用素というものを使うことで見事に「リーマン予想」(通称“ヴェイユ予想”)が解決されました。
このように、リーマン予想解決にむけて様々な一般化や、考え方、哲学が広がっていきましたが、2020年現在でもまだ本家のリーマン予想は解決していません。しかし、解決に向けて生み出されたさまざまな数学の概念や手法というのは、間違いなく数学や物理といった科学全般に大いに貢献しています。この先の未来にも思わぬ科学の発展につながる発見があるかもしれません。
贅沢を言っていいのであれば、生きているうちにリーマン予想解決を目の当たりにしたいものです(本音)。
　

<文/岡本健太郎>
⇒ 講師紹介ページへ