１．ミレニアム懸賞金問題

数学って、なんだか研究しつくされてこれ以上計算することなんてないのではないじゃないか？
そう思う人もたくさんいらっしゃると思います。
しかし、実は現代の数学でもまだまだ未解決の問題が多く、逆に「ほとんど何もわかっていない」と主張する数学者もいるほどなのです！
そこで、今回は未解決問題の中でも有名な「ミレニアム懸賞金問題」についてご紹介していきたいと思います。
ミレニアム懸賞金問題とは、2000年にアメリカのクレイ数学研究所が発表した７つの未解決問題のことで、それぞれ懸賞金として100万ドルがかけられているのです。なんだかお尋ね者みたいですよね。
その“お尋ね者”を見ていきましょう。

1.ヤン-ミルズ方程式と質量ギャップ問題
2.P≠NP問題
3.ナビエ-ストークス方程式の解
4.ホッジ予想
5.ポアンカレ予想
6.バーチ-スウィンナートン=ダイア―予想
7.リーマン予想

どれも難しそうですね…。というより、何を言っているのかさっぱりわからない人もいるでしょう。詳しい内容は省略しますが、⑤のポアンカレ予想というのは「ものの形」についての問題で、いわゆる幾何学と呼ばれる分野になります。このポアンカレ予想、実は2006年にグレゴリー・ペレルマンによって見事解決されています。しかも驚くべきことに、ペレルマンは懸賞金100万ドルの受け取りを断っているのです。孤高の数学者ペレルマン。彼がなぜ受け取りを拒否したのか、そこにどういったドラマがあったのか。こういったお話はまた機会があれは本ブログにてご紹介できればと思っています。

さて、懸賞金問題の後半にでてくる「～予想」とはどういったものかというと、ざっくり言えば、「～であるだろう」といった形の問題です。
こういった形の問題には基本的に

・予想が正しいのであれば「証明」を与える。
・予想が間違いであれば証拠となる「具体例」を与える。

といった答え方になります。

今回はこの問題の中で最も難しいといわれている「リーマン予想」について詳しく取り上げいきたいと思います。解くことは難しいとされていますが、予想の内容や主張に関しては7つのうち最もわかり易いといわれています。このブログでは、何回かに分けて、「リーマン予想」が何なのか、どう難しいのか、解けたら何がわかるのかなどを、なるべく難しい表現はなしで本質的な部分をお伝えしようと思います。

２．因数分解

みなさんは「因数分解」を覚えていらっしゃいますか？中学や高校のときにやったアレです。
例えば

$$x^2+x=x(x+1)\\
x^2-3x+2=(x-1)(x-2)$$

といった、“式の整理整頓作業”のことです。
また、x がどんな点にあるとき関数が0(ゼロ)になるのかを考えるとき、因数分解した形を見るとわかり易くなります。

$$x^2-3x+2=(x-1)(x-2)=0$$

とすると、/(x=1,x=2\)のときに\(0\)になるのがわかります。こういった「\(0\)になるような点」のことを、その関数のゼロ点といいます。
ここで注目していただきたいのが、
ゼロ点さえわかれば関数がほぼ復元できる
という点です。
つまり、「\(x=1,x=2\)のときに0になりますよ」という情報だけで、その関数は

$$(\mbox{定数})×(x-1)(x-2)$$

という形に決定できます。これを「因数定理」といいます。
なお「定数」の部分は一番次数の高い係数さえわかれば決定できるので完全に関数を復元できます。
この節でおさえていただきたいポイントは
ゼロ点の情報で、関数をある程度復元できる！

です。次の節では、ゼロ点を把握する上で重要になってくる「方程式」についてお話していきます。

３．方程式

第2節で少し登場しました方程式のお話に入ります。方程式とは人類の歴史からみても必要とされ、生まれた分野とも言えます。
たとえば、

これは方程式

$$x+3=10$$

を解くことにより\(x=7\)が得られます。こういったものを数えるための数を自然数といいます。では、式の数字を入れ替えて

$$x+10=3$$

という方程式はどうでしょう？リンゴは何個あったのか。
すると途端に答えが出て来なくなります。「\(-7\)個」なんてないからです。
この式を解くためには「マイナス」や「ゼロ」といった概念が必要になってきます。
これが整数の誕生です。
こうして方程式が解けるように、数は時代の流れとともに拡張されていきます（「発見」という表現の方が適切かもしれません）。
その後、
3x=7
が解けるように「分数（有理数）」が生まれ、2次の最も基本的な形の方程式

$$x^2=2$$

が体系的に解けるように√（ルート）といったものが発明されました。
こうして、小数点が不規則に無限に続くような実数（無理数）を合わせて実数という世界が出来上がりました。
しかし、

$$x^2=-2$$

などのように、右側の数がマイナスの値をとるとき、答えが出ません…。
この問題を解決するために、

$$i^2=-1$$

を満たす数\(i\)が発明されました。この\(i\)を虚数といい、

$$a+bi$$

の形の数を複素数と言います。この数を使えば、どんな2次方程式も解くことができます。
言い換えると、2次関数のゼロ点を保証することができます。実は2次関数に限らず、どんな関数も複素数を使ってゼロ点を表すことができます。
例えば3次関数の場合は3つ、4次関数の場合は4つ、一般にn次関数の場合は\(n\)個のゼロ点の存在が保証されます。

４．リーマン予想とは

イタリア人数学者ピエトロ・メンゴリは次のような足し算の和について考えました。

ご覧の通り、終わりなく永遠に数を足していくわけですが、どんどん足される数が小さくなっていくことから、実はある値に近づいていくことが古くから知られていました。
実際に1.644934…といった値になることは近似的にわかっていました。
しかし、これが具体的にどんな値なのか、長い間未解決問題だったのです。
メンゴリが1644年に問題を提起して91年後。この問題はついに解決しました。解決したのはかの有名なレオンハルト・オイラー。人類史上最も多くの論文を残した超人的数学者です。この功績をたたえ、この問題は彼の故郷「バーゼル」から名前をとり「バーゼル問題」と言われています。

オイラーが導き出したその答えは

$$\frac{1}{1^2} +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\frac{1}{5^2} +\cdots=\frac{\pi^2}{6}$$

です。
ちょっと待ってください。\(\pi\)といえばそう、円周率です。

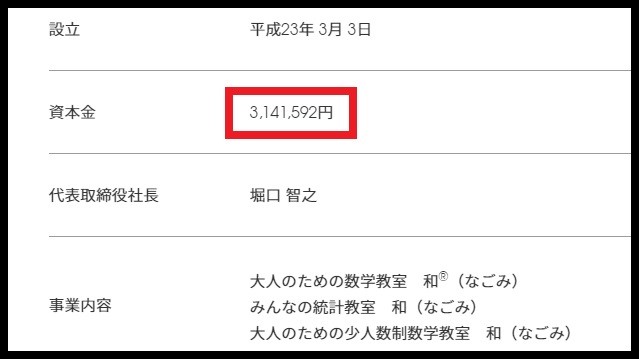
そう。弊社の資本金でもあります。
※点の位置がポイントです。
つまり、バーゼル問題の答えは弊社資本金の\(2\)乗を\(6\)で割った値だったのです！

またオイラーは次のような驚愕の公式を発見しました。

右辺はなんと素数たちしか現れません。
素数とは数の世界の原子のようなもので、それ以上割り切れない数のことをいいます。素数は規則がわかっておらず、古代から未解決な事柄として有名でした。
とにかくまとめると、上のような無限の足し算は、素数たちの掛け算で表現することができるというのです。

円周率という、幾何学的な数字が表れるのも突拍子もなかったのですが、素数の登場も非常に驚きです。この無限の足し算はこの“円と素数の不思議な関係”を結び付けているといえるのです。

この無限の足し算を「複素数の関数」として初めて扱ったのが、ベルンハルト・リーマン。
ドイツの天才数学者です。39歳という短い人生でしたが、彼の数学は非常に先駆的で、現代の数学に大きく影響を及ぼしています。
リーマンはバーゼル問題の足し算を一般化し

$$\zeta(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\cdots$$

というゼータ関数を考えました。つまり、バーゼル問題は

$$\zeta(2)=\frac{\pi^2}{6}$$

と表されます。またこの関数は、

を満たします。つまり、しっかり素数との関係も残っています。
第2節でご紹介したように、ゼロ点は関数の情報を多く持っています。つまり、ゼータ関数のゼロ点はゼータ関数の情報をもっており、ゼータ関数は素数の情報を持っています。
つまり、ゼータ関数のゼロ点は素数の情報を多く持っていることになるのです！

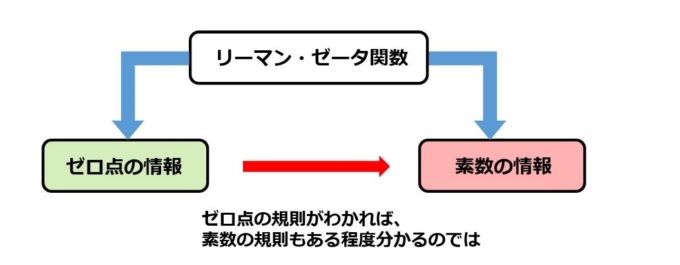
言い換えると、ゼロ点の規則がわかれば、素数の規則もつかめるのではないかということです。
なお、負の偶数点はゼータ関数のゼロ点になっていることがしられており、このゼロ点はあまり有益な情報をもっておらず、「自明ゼロ点」と言われています。
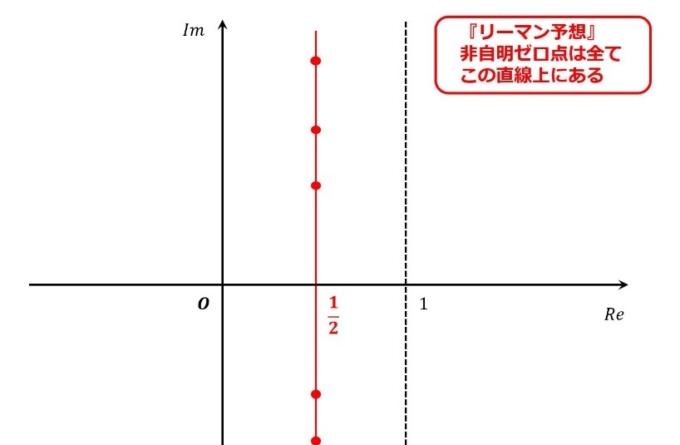
リーマン予想はこの自明ゼロ点以外のゼロ点（非自明ゼロ点）の規則性に関する予想です。

最後に今世紀最大の超難問「リーマン予想」の主張を紹介して終わりにしたいと思います。

いかがでしたでしょうか。リーマン予想の主張自体は比較的にシンプルなのですがこれがなかなか解けず、今現在でも世界中で研究者たちを悩ませています。
前編では、リーマン予想が何を言っているのかについて簡潔にまとめてみました。
後編ではこの予想について、もう少しマニアックな話題に触れて詳しくお話していこうと思います。

<文/岡本健太郎>
⇒ 講師紹介ページへ