データの関係性を読み取る指標「相関係数」の性質②

統計・機械学習トピック

公開日

2025年2月10日

更新日

2025年2月9日

　みなさんこんにちは！和からの数学講師の岡本です。今回のマスログは前回に引き続き、相関係数について解説していきます。前回のマスログはこちら↓

データの関係性を読み取る指標「相関係数」の性質①

前回は相関係数の定義や計算方法について説明しました。今回は定義された相関係数が-1～+1の範囲の値をとる理由と、相関係数の別の捉え方について解説してきます！

この記事の主な内容

１．相関係数の定義と計算（復習）

　まずは、相関係数の定義を復習しておきましょう。\(x\)と\(y\)のデータの標準偏差をそれぞれ\(s_x, s_y\)とし、共分散を\(s_{xy}\)とします。このとき、２つのデータの相関係数\(r_{xy}\)は次で定められます。

\begin{align*}
r_{xy}:=\frac{s_{xy}}{s_x s_y}.
\end{align*}

なお、標準偏差や共分散は\(n\)個のデータの組\(x_1,x_2, \ldots, x_n, y_1, y_2,\ldots, y_n\)を用いて

\begin{align*}
s_x=\sqrt{\frac{1}{n}\sum_{k=1}^n (x_k-\bar{x})^2}, s_y=\sqrt{\frac{1}{n}\sum_{k=1}^n (x_k-\bar{x})^2}, s_{xy}=\frac{1}{n}\sum_{k=1}^n (x_k-\bar{x})(y_k-\bar{y})
\end{align*}

と計算できます（ここで\(\bar{x}, \bar{y}\)はそれぞれのデータの平均値を表します）。したがって相関係数は

\begin{align*}
r_{xy}=\frac{\frac{1}{n}\sum_{k=1}^n (x_k-\bar{x})(y_k-\bar{y})}{\sqrt{\frac{1}{n}\sum_{k=1}^n (x_k-\bar{x})^2}\cdot \sqrt{\frac{1}{n}\sum_{k=1}^n (y_k-\bar{y})^2}}=\frac{\sum_{k=1}^n (x_k-\bar{x})(y_k-\bar{y})}{\sqrt{\sum_{k=1}^n (x_k-\bar{x})^2}\cdot \sqrt{\sum_{k=1}^n (y_k-\bar{y})^2}}
\end{align*}

となり、分母分子で\(1/n\)が相殺されます。そのため実際に計算する際は毎回データの個数で割る必要はなくなるわけです。

２．相関係数の値とコーシー・シュワルツの不等式

　相関係数は共分散を標準偏差で割ることで定義されましたが、このように定めることで-1～+1の範囲しかとらなくなります。この理由は「コーシー・シュワルツの不等式」で説明できます。コーシー・シュワルツの不等式とは、\(n\)の実数の組\(a_1,a_2, \ldots, a_n, b_1, b_2, \ldots,b_n\)に対して成り立つ次の不等式を指します。

\begin{align*}
(a_1b_1+a_2b_2+\cdots+a_nb_n)^2\leq(a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2).
\end{align*}

対称的で非常に美しい不等式です。例えば\(n=2\)のとき、右辺から左辺を引く計算を行うと

\begin{align*}
(a_1^2+a_2^2)(b_1^2+b_2^2)-(a_1 b_1+a_2 b_2)^2=(a_1b_2)^2-2a_1 b_2 a_2 b_1+(a_2 b_1)^2=(a_1 b_2-a_2 b_1)^2 \geq 0
\end{align*}

と、差が正になることから不等式が正しいことが確認できます。これが一般の\(n\)に対して成り立つというのがコーシー・シュワルツの不等式です。\(a_k=x_k-\bar{x}, b_k=y_k-\bar{y}\)とすれば、コーシー・シュワルツの不等式により

\begin{align*}
\Bigg(\sum_{k=1}^n(x_k-\bar{x})(y_k-\bar{y})\Bigg)^2\leq \Bigg(\sum_{k=1}^n(x_k-\bar{x})^2\Bigg) \Bigg(\sum_{k=1}^n(y_k-\bar{y})^2\Bigg)
\end{align*}

となります。平方根をとり、両辺を割ることで、最終的に以下の不等式を得ることができます。

\begin{align*}
-1\leq \frac{\sum_{k=1}^n (x_k-\bar{x})(y_k-\bar{y})}{\sqrt{\sum_{k=1}^n (x_k-\bar{x})^2}\cdot \sqrt{\sum_{k=1}^n (y_k-\bar{y})^2}}\leq 1
\end{align*}

真ん中の式は先ほど確認したように、\(x\)と\(y\)の相関係数\(r_{xy}\)であり、確かに-1～+1の範囲をとることがわかります。なお、\(n\)個の場合のコーシー・シュワルツの不等式の証明はいくつか知られていますが、2次関数程度の知識でも証明することができます。

感銘を受けた数学「美しき不等式たちの世界～ヤング、ヘルダー、ミンコフスキーまで～」

データ分析小話～平均値と中央値の差について～

３．ベクトルから見た相関係数

　話は変わりますが、高校数学で登場する「ベクトル」という分野には「内積」という概念があります。具体的に２つのベクトル\(\vec{a}, \vec{b}\)と、そのなす角を\(\theta\)とおくと、\(\vec{a}, \vec{b}\)の内積は,

\begin{align*}
\vec{a}\cdot \vec{b}:=|\vec{a}||\vec{b}|\cos \theta
\end{align*}

で定められます。ここで\(|\vec{a}|\)はベクトル\(\vec{a}\)の大きさを表します。また、\(n\)次元空間内でベクトルが成分で表されているとき、内積は

\begin{align*}
\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+\cdots+a_nb_n
\end{align*}

という形で表現できます。ベクトルの大きさは\(|\vec{a}|=\sqrt{a_1^2+\cdots+a_n^2}\)で表されることから、ベクトルの内積は２通りで表現することができます。

\begin{align*}
|\vec{a}||\vec{b}|\cos \theta=\sqrt{a_1^2+\cdots +a_n^2}\sqrt{b_1^2+\cdots+b_n^2}\cos \theta=a_1b_1+\cdots+a_nb_n=\vec{a}\cdot \vec{b}
\end{align*}

両辺をベクトルの大きさで割ると

\begin{align*}
\cos \theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}
\end{align*}

となります。２つのベクトルが同じような方向を向いているとき、“なす角”は0度に近く、\(\cos\)の値は+1に近い値になります。また、２つのベクトルが反対向きになっているとき、“なす角”は180度に近いため、\(\cos\)の値は-1に近い値になります。さらに、２つのベクトルが全く互いに関係しない方向である（＝直交している）とき、“なす角”は90度に近く、\(\cos\)の値は0付近の値になります。このように、２つのベクトルがどれだけ「似ている」かを測るために\(\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\)の値を利用することがあります。この値を\(\cos\)類似度と呼びます。

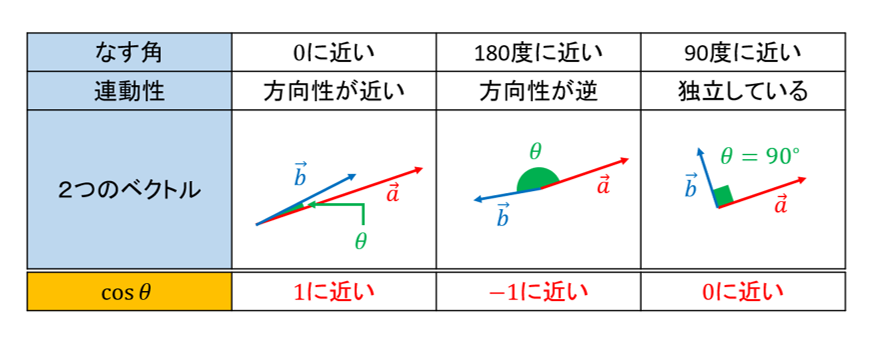
もうお気づきかもしれませんが、\(a_k=x_k-\bar{x}, b_k=y_k-\bar{y}\)とすれば、上の式は相関係数に他なりません。つまり、相関係数は\(\cos\)類似度の一種であることがわかります。たしかにベクトルが同じ方向を向いているというのは「正の連動」＝「正の相関」に対応し、真逆を向いていることは「負の連動」＝「負の相関」、直交しているとは「無相関」であることに対応します！このように、相関係数はベクトルという視点で捉えるととても理にかなった面白い指標であることがわかります。

４．さいごに

　いかがでしたでしょうか。今回は相関係数を数学的に捉えるという話をしてみました。数学的な背景を知ることでデータサイエンスや統計学で用いられる分析手法や指標の重要性や意味が大きく理解できるようになります！特に、今回ご紹介した「\(\cos\)類似度」は、例えば通販サイトで購入した商品に関連性が高い、いわゆる“おすすめ商品”が表示される仕組みなど、身近なところに使われています。和からでは、こうした高校や大学以上の数学や統計学を身近な例を通して学習することができます。個別指導では、お客様に合った授業が実現できるように柔軟に対応することができます。1対1のマンツーマン授業に興味のある方はぜひ一度無料カウンセリングにご参加ください！