感銘を受けた数学「美しき不等式たちの世界~ヤング、ヘルダー、ミンコフスキーまで~」
公開日
2020年8月1日
更新日
2025年9月17日
こんにちは。和からの数学講師の岡本です。以前、「感銘を受けた数学」シリーズとして、岡本が狂おしいほど好きなオイラーの五角数定理、三平方の定理の証明たちをマスログでご紹介しました。
今回も岡本がグッと来た数学をご紹介していこうと思います。今日は「不等式」についてです。AよりBの方が「大きい」ことを
\begin{align*}A<B\end{align*}
と表現します。数学の世界では、値が変化していく関数や数列における不等式に特に興味があります。不等式にはいろんな種類があり、今回はその中で特に面白く美しいものをご紹介いたします。
この記事の主な内容
1.凸不等式
数学用語で「凸」というものがあります。
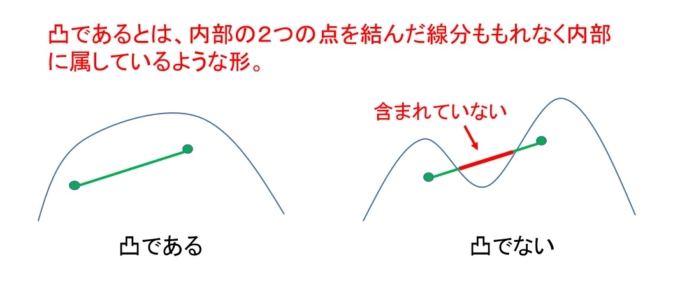
上の図のように「谷」の部分が含まれない曲線の事をいいます。こうした「凸」という性質を使った不等式があり、総じて「凸不等式」と呼びます。考え方は非常にシンプルです。下の図をご覧ください。
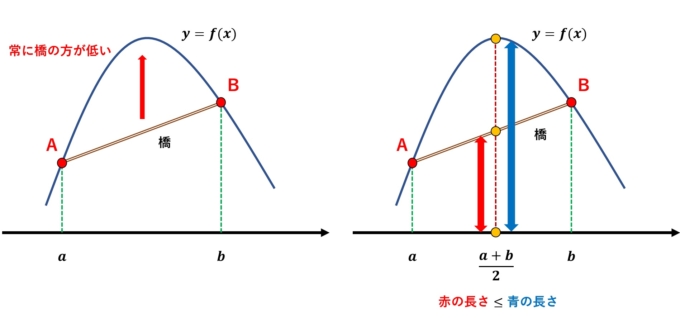
凸な関数\(y=f(x)\)があると、中で結んだ「橋」は、関数の値と比べて常に低い位置にあることがわかります。これを利用することで、\(a\)と\(b\)の内分点(上の例では1:1の内分点=中点)に対して上下関係が成り立ちます。上の例では
\begin{align*}\frac{f(a)+f(b)}{2}\leq f(\frac{a+b}{2})\end{align*}
が成り立ちます。この不等式のすごいところは区間\([a, b]\)上で関数\(f(x)\)が上向きに凸であれば常に成り立ちます。非常に応用の多い不等式です。
2.そうか、そうかの相乗平均
次の話題は相加・相乗平均の不等式についてです。高校数学や大学入試問題で、忘れたころに現れ、その都度を苦しめられる不等式の一つです。個人的に「そうか、そうかの相乗平均」と呼んでいます(特に意味はありません)。この不等式も非常に面白いものですが、まずは「相加平均」と「相乗平均」についてご紹介いたします。
2つの正の実数\(a, b\)があるとします。この2つの数に対して、「足し算的な平均」と「掛け算的な平均」を考えます。足し算(加法)的な平均というのは、数を足し上げて、足した数の個数で割るという、いわゆる普通の平均で、正確には相加平均といいます。
\begin{align*}\frac{a+b}{2}\end{align*}
対して掛け算的な平均とは、2つの数を掛け合わせます。こうすることで数としては「2つ」かけられた状態なので、これの平方根をとることで掛け算(乗法)的に中間的な値になります。これが相乗平均です。
\begin{align*}\sqrt{ab}\end{align*}
この2種類の平均には面白い性質があり、\(a, b\)が正であれば次が成り立ちます。
\begin{align*}\sqrt{ab}\leq\frac{a+b}{2}\end{align*}
これがいわゆる「相加・相乗平均の不等式」です。\(a=b\)のときのみ等号が成立します。
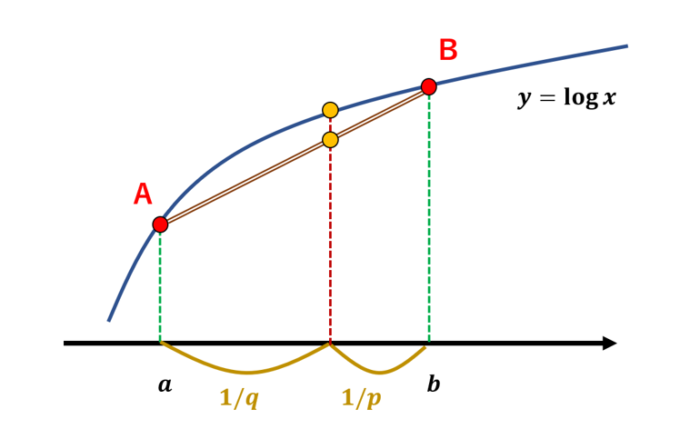
ちなみにこの不等式は上で示した凸不等式を用いることで簡単に証明できます。実際に対数関数\(y=\log x\)は全ての\(x>0\)について上に凸であることが知られており
\begin{align*}\frac{\log a+\log b}{2}\leq\log(\frac{a+b}{2})\Longleftrightarrow \log (ab)^{1/2} \leq\log(\frac{a+b}{2})\end{align*}
が成り立ちます。対数の中を比べると相加・相乗平均の不等式が得られますのです!エレガントですね!
なお、相加相乗平均の不等式は一般に\(n\)個の正の実数に対しても成り立ちます。
\begin{align*}(a_1a_2\cdots a_n)^{1/n}\leq \frac{a_1+a_2+\cdots+a_n}{n}\end{align*}
3.コーシー・シュワルツの不等式
次にご紹介するのはコーシー・シュワルツの不等式です。2対の実数のペア\((a_1,a_2)\)と\((b_1,b_2)\)を用意します。このとき常に次の不等式が成り立ちます。
\begin{align*}(a_1b_1+a_2b_2)^2\leq (a_1^2+a_2^2)(b_1^2+b_2^2)\end{align*}
非常に対称的で美しい不等式です。これを「コーシー・シュワルツの不等式」と呼びます。直接大きい方から小さい方を引いて証明することもできますが、実はベクトルの内積を使ったとらえ方が最も自然なのです。実際、2対の実数のペア\((a_1,a_2)\)と\((b_1,b_2)\)をベクトル\(\mathbf{a}, \mathbf{b}\)と考えます。このとき、2つのベクトルのなす角を\(\theta\)としたとき、内積は
\begin{align*}\mathbf{a}\cdot \mathbf{b}=\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}\cos \theta\end{align*}
と表せます。またベクトルの成分表示を使った表し方と、常に\(\cos \theta \leq 1\)であることから
\begin{align*}a_1b_1+a_2b_2=\sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}\cos \theta \leq \sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}\end{align*}
となり、両辺を2乗することでコーシー・シュワルツの不等式が得られます。
なお、コーシー・シュワルツの不等式は一般の\(n\)次元ベクトル空間でも一般化されます。
\begin{align*}\left\{\sum_{k=1}^{n}a_kb_k\right\}^2\leq \left\{\sum_{k=1}^{n}a_k^2\right\}\left\{\sum_{k=1}^{n}b_k^2\right\}\end{align*}
さらには、有限次元に限らず、無限次元の関数空間(例えば2乗可積分関数空間)でもコーシー・シュワルツの不等式が考えられます。
\begin{align*}\left|\int f(x)g^*(x)dx\right|^2\leq \int |f(x)|^2dx \int |g(x)|^2dx \end{align*}
恐ろしくつよつよな不等式なのです…!
4.不等式3兄弟
続いて、ヤング、ヘルダー、ミンコフスキーの”不等式3兄弟”をご紹介いたします。まずは三男坊の「ヤングの不等式」から。\(1/p+1/q=1\)を満たす正の実数\(p,q\)を用意します。このとき正の実数\(a,b\)に対して次が成り立ちます。
\begin{align*}a^{\frac{1}{p}}b^{\frac{1}{q}}\leq \frac{1}{p}a+\frac{1}{q}b\end{align*}
こちらも対称性があり、とても美しい不等式です。これをヤングの不等式と言います。証明は簡単で、最初にお話した凸不等式を使えば示されます。実際に関数を\(f(x)=\log x\)として、\(x=a,b\)の間を\(1/q:1/p\)に内分した点で不等式を立てると終わりです。
続いては、ヘルダーの不等式。ヤングの不等式のときと同様に\(1/p+1/q=1\)を満たす正の実数\(p,q\)を用意します。このとき正の実数のペア\((a_1,a_2)\)と\((b_1,b_2)\)について次が成り立ちます。
\begin{align*}a_1b_1+a_2b_2\leq (a_1^p+a_2^p)^{\frac{1}{p}}(b_1^q+b_2^q)^{\frac{1}{q}}\end{align*}
見覚えありまえんか?そうなんです、\(p=q=2\)とするとこれはコーシー・シュワルツの不等式に他なりません!つまり、ヘルダーの不等式はコーシー・シュワルツの不等式の親戚だったわけです!
そしてその証明が非常にファビュラスなんです!ヤングの不等式における\(a, b\)を次のように設定すると
\begin{align*}a=\frac{a_1^p}{a_1^p+a_2^p}, b=\frac{b_1^q}{b_1^q+b_2^q}\Longrightarrow \frac{a_1}{(a_1^p+a_2^p)^{1/p}}\frac{b_1}{(b_1^q+b_2^q)^{1/q}}\leq \frac{1}{p}\frac{a_1^p}{a_1^p+a_2^p}+\frac{1}{q}\frac{b_1^q}{b_1^q+b_2^q}\\a=\frac{a_2^p}{a_1^p+a_2^p}, b=\frac{b_2^q}{b_1^q+b_2^q}\Longrightarrow \frac{a_2}{(a_1^p+a_2^p)^{1/p}}\frac{b_2}{(b_1^q+b_2^q)^{1/q}}\leq \frac{1}{p}\frac{a_2^p}{a_1^p+a_2^p}+\frac{1}{q}\frac{b_2^q}{b_1^q+b_2^q}\end{align*}
が得られます。2つの不等式を足し合わせることで、
\begin{align*}\frac{1}{(a_1^p+a_2^p)^{1/p}(b_1^q+b_2^q)^{1/q}}(a_1b_1+a_2b_2)\leq \frac{1}{p}\frac{a_1^p+a_2^p}{a_1^p+a_2^p}+\frac{1}{q}\frac{b_1^q+b_2^q}{b_1^q+b_2^q}=\frac{1}{p}+\frac{1}{q}=1\end{align*}
よって、ヘルダーの不等式が証明されます!最後に右辺が1になる瞬間がたまらなく好きです。。。!
ちなみに同様のやり方で、次のような一般の場合を示すことができます。
\begin{align*}\sum_{k=1}^{n}a_kb_k \leq \left\{\sum_{k=1}^{n}a_k^p \right\}^{1/p}\left\{\sum_{k=1}^{n}b_k^q \right\}^{1/q}\end{align*}
さて、最後にミンコフスキーのアニキの登場です。実数\(p \geq 1\)を用意します。このとき正の実数のペア\((a_1,a_2)\)と\((b_1,b_2)\)について次が成り立ちます。
\begin{align*}((a_1+b_1)^p+(a_2+b_2)^p)^{1/p}\leq (a_1^p+a_2^p)^{1/p}+(b_1^p+b_2^p)^{1/p}\end{align*}
これがミンコフスキーの不等式(アニキ)です。個人的にこの不等式は大好きで、大学の図書館で感動して涙を流した記憶があります。さてアニキの証明がそう簡単にはいきません。というより、知らないとできないレベルのテクニカルな証明になります。
まず、次のような変形をします。
\begin{align*}&(a_1+b_1)^p+(a_2+b_2)^p\\&=a_1(a_1+b_1)^{p-1}+b_1(a_1+b_1)^{p-1}+a_2(a_2+b_2)^{p-1}+b_2(a_2+b_2)^{p-1}\end{align*}
ここで、右辺の第1項と第3項に関して\(p, q=\frac{p}{p-1}\)におけるヘルダーの不等式を用いると
\begin{align*}a_1(a_1+b_1)^{p-1}+a_2(a_2+b_2)^{p-1}\leq (a_1^p+a_2^p)^{\frac{1}{p}}((a_1+b_1)^p+(a_2+b_2)^p)^{\frac{p-1}{p}}\end{align*}
同様に右辺に第2項、第4項に対してもヘルダーの不等式より
\begin{align*}b_1(a_1+b_1)^{p-1}+b_2(a_2+b_2)^{p-1}\leq (b_1^p+b_2^p)^{\frac{1}{p}}((a_1+b_1)^p+(a_2+b_2)^p)^{\frac{p-1}{p}}\end{align*}
が成り立ちます。辺々を足すことにより、
\begin{align*}&(a_1+b_1)^p+(a_2+b_2)^p\leq ((a_1^p+a_2^p)^{\frac{1}{p}}+(b_1^p+b_2^p)^{\frac{1}{p}})((a_1+b_1)^p+(a_2+b_2)^p)^{\frac{p-1}{p}}.\end{align*}
見えましたでしょうか。そうなんです、両辺を\(((a_1+b_1)^p+(a_2+b_2)^p)^{\frac{p-1}{p}}\)で割れば、ミンコフスキーの不等式が舞い降りてきます。
ちなみに、どうようの方法で一般の場合も成り立ちます。
\begin{align*}\left\{\sum_{k=1}^n(a_k+b_k)^p\right\}^{1/p}\leq \left\{\sum_{k=1}^na_k^p\right\}^{1/p}+\left\{\sum_{k=1}^nb_k^p\right\}^{1/p}\end{align*}
そしてふと気づくと、\(p=2\)のとき、これは平面内で「寄り道をすれば歩く距離は遠くなる」ことを意味する「三角不等式」に他なりません!
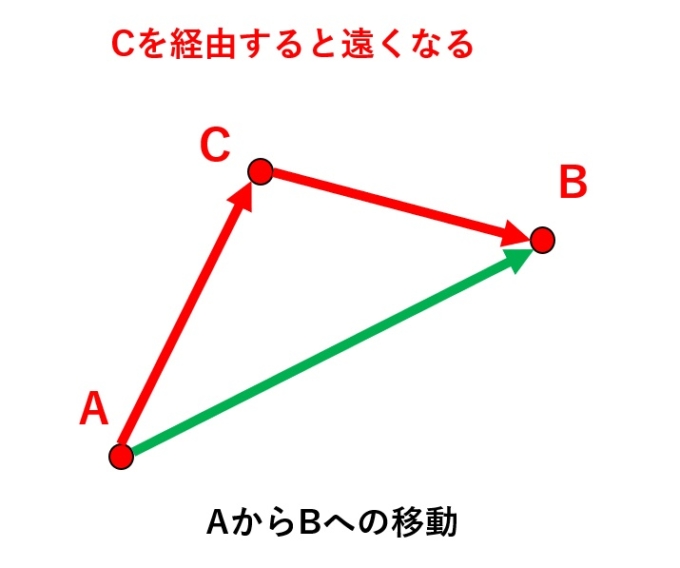
実際に\(L_p-\)距離という概念があり、その空間における三角不等式こそ、ミンコフスキーの不等式なのです。
5.さいごに
いかがでしたでしょうか。今日は不等式の奥深い世界を少しだけご紹介いたしました。どんなに複雑で難解に見える等式、不等式であってもその多くは非常にシンプルな解釈やアイデアから来ています。日常生活においても、普段「当たり前だ」と思っていることでも少し考え方を変えるだけで素敵なアイデアは生まれるかもしれません!今回のでてきた不等式については、古典的で有名不等式たちがまとめて載っている、以下の本がおすすめです。
不等式 (数学のかんどころ 9) 大関 清太 (著) 共立出版
また、代数的な観点から最先端の不等式の理論に関しては以下の本が非常に面白いと思います。
不等式―21世紀の代数的不等式論 安藤 哲哉 (著) 数学書房
今回扱った「関数の解析」の基礎となるのは微分・積分です。微分積分の基礎から学びなおしたいという方はこちら!「目で見てわかる」を意識した微積分学の新たな学びかたをお手伝いいたします。
また今回ご紹介した証明の美しさ。これは数学の一つの魅力だと思います。こうした「美しさ」やデザイン、Excelアートに関する無料セミナーも開催しておりますので、興味のある方は是非ご参加ください。
また、岡本の数学アート作品、デザイングッズはこちらから
和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。
<文/岡本健太郎>