データの関係性を読み取る指標「相関係数」の性質①

統計・機械学習トピック

公開日

2025年2月2日

更新日

2025年2月1日

　みなさんこんにちは！和からの数学講師の岡本です。本日はデータの関係性を表す指標として使われる「相関係数」について、数学的な構造を見ていこうと思います。データ分析の世界では当たり前のように使われる相関係数、その魅力に迫っていきます！

統計に関する無料セミナーはこちら！

文系のための「統計超入門セミナー」-目で見てわかるビジネス統計学-

この記事の主な内容

１．データの関係性を見るために

「身長（cm）」と「体重（kg）」のように、２つの数値のデータ\(x, y\)の関係性を考えてみます。一般に、身長の高い人はその分体重も大きくなると予想されます。実際に散布図を描いてみると「右肩上がり」の傾向が見て取れます。このように、「\(x\)のデータが増加すれば、\(y\)のデータも増加する」ような関係性を「正の相関」、逆に「\(x\)のデータが増加すれば\(y\)のデータは減少する」ような関係性を「負の相関」といいます。つまり大きく２つのパターンの連動性を符号で表現していると考えます。ただし、関係性にも強さや弱さというものがあります。

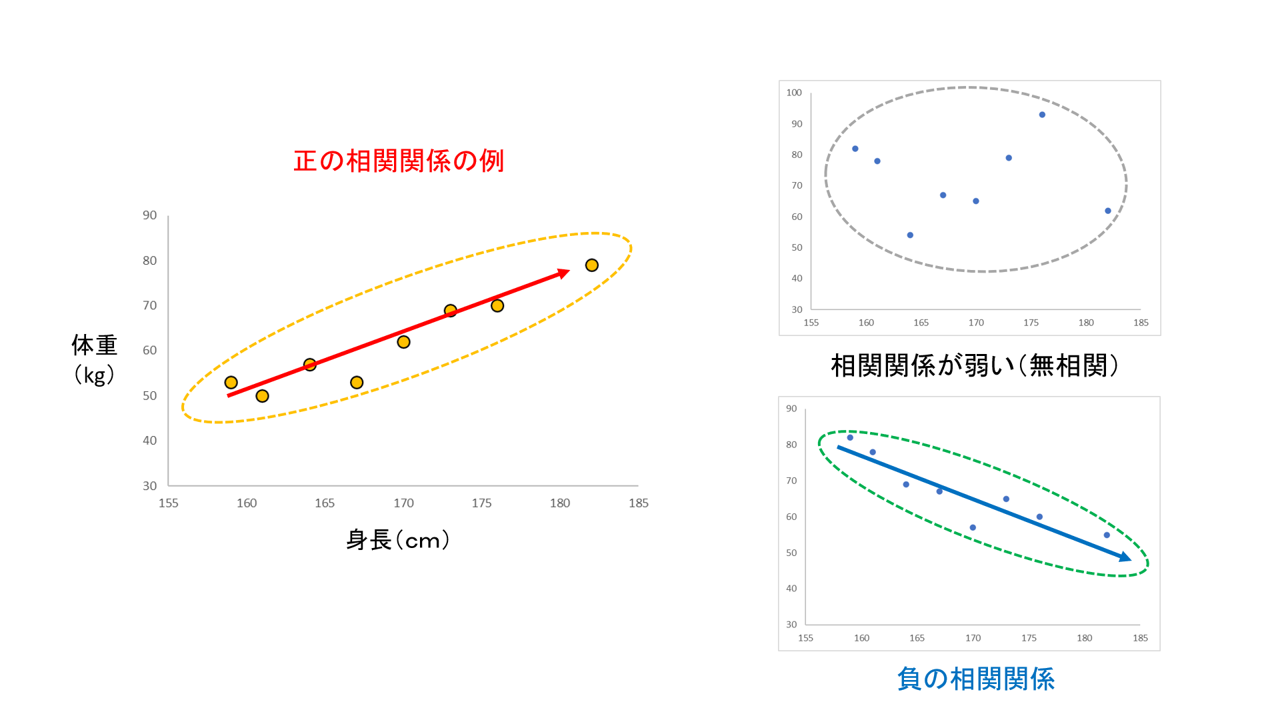
散布図の点の配置がぼやけていると、関係性が「弱い」と考えられ、直線的な関係性がはっきりしているときは関係性が「強い」と考えます。こうした関係性の強弱を数値化したものとして「相関係数」という指標があります。相関係数は＋１から－１までの数値を取り、＋１に近いほど正の相関が強く、－１に近いほど負の相関が強いと対応付けられ、0に近いときはそもそも「相関関係がない」と判断できます。相関係数はその数値だけで、データの関係性を表現できるので非常に便利な指標となっています。

２．相関係数の定義

　では、相関係数とはどのように計算されるものなのでしょうか？その定義について踏み込んでみようと思います。まず、２つのデータ\(x, y\)を用意します。データの標準偏差をそれぞれ\(s_x, s_y\)とし、\(x, y\)の共分散を\(s_{xy}\)とすると、\(x\)と\(y\)の相関係数\(r_{xy}\)は次で定められます。

\begin{align*}
r_{xy}:=\frac{s_{xy}}{s_x s_y}.
\end{align*}

相関関係が正か負かといった傾向は、実は共分散\(s_{xy}\)の値で把握できます。これについて少し説明しておきましょう。散布図におけるデータの“平均の位置\((\bar{x}, \bar{y})\)”が原点にくるように、すべてのデータを平行移動させます。移動した点たちが第1、第3象限（①）に多いときは「正の相関」傾向、第2、第4象限（②）に多いときは「負の相関」傾向があると考えることができます。そこで移動した点の\(x\)座標と\(y\)座標を掛け合わせた点の符号を見れば、その点が①と②のどちらのエリアに位置しているのかがわかります。これらを掛け合わせた値（偏差積）の平均値を共分散\(s_{xy}\)と定めているので、共分散の値が正であれば、点は\((\bar{x}, \bar{y})\)を中心に右肩上がりの配置、負であれば右肩下がりの配置であることがわかります。

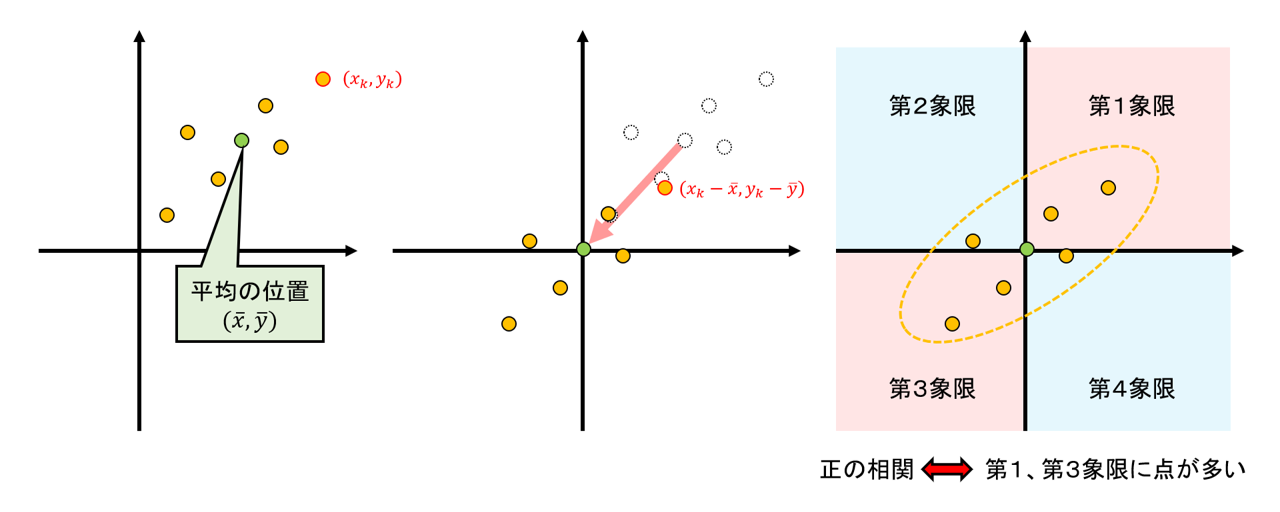
　しかし、共分散の値は、データの値を定数倍すると変わってしまいます。例えば、身長の単位をcmからmに変えるとき、数値は0.01倍されます。このとき共分散の値も0.01倍されてしまうため、共分散の値の大小に関係性の強さを読み取ることはできません。そこで、データを定数倍すると同じく定数倍される標準偏差との比を考えることで、「データを定数倍しても変化しない指標」を考えることができます。

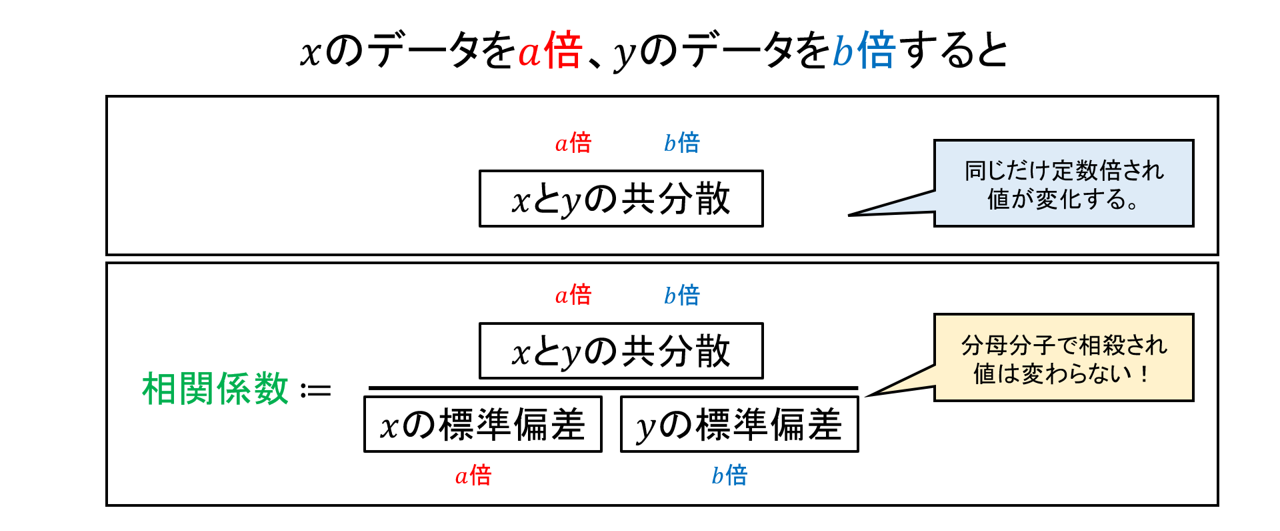
※例えばデータを定数倍すると平均値も同じだけ定数倍されるため、これを分母と設定することも考えられますが、平均値はデータを平行移動する（同じ量だけ足し引きをする）ことによって変化してしまいます。共分散や標準偏差は平行移動で変化しない値なので、これらの比は指標として考えるうえで適切であると考えられます。

３．相関係数の取りうる値

データの相関関係を適切に評価する指標として備えておきたい性質をまとめます。

　①データを定数倍しても変化しない指標
　②データを平行移動しても変化しない指標
　③値の限界値が設定されている指標

　確率や内訳、比率のように「0~1まで」といった値の限界値が設定されている方が、強さや弱さの比較がわかりやすいです。実は共分散を標準偏差で割ることで、取りうる値が-1~+1となることがわかっています。そのためこの指標がデータ間の関係性を表現する指標として適切であると考えられます。なお、-1~+1の間の値しか取らないことはそんなに明白なことではありませんが、数学を用いてきちんと証明することができます！

４．さいごに

　いかがでしたでしょうか。今回はどうして相関関係を適切に表すことができるのかについて簡潔にお話をしてきました。次回は、相関係数がなぜ-1から+1までの値しか取らないのか、また「相関係数の驚くべき正体」について解説していきたいと思います。和からでは、こうした高校や大学以上の数学を個別授業形式が学習することができます。お客様に合った授業が実現できるように柔軟に対応することができます。個別授業に興味のある方はぜひ一度無料カウンセリングにご参加ください！