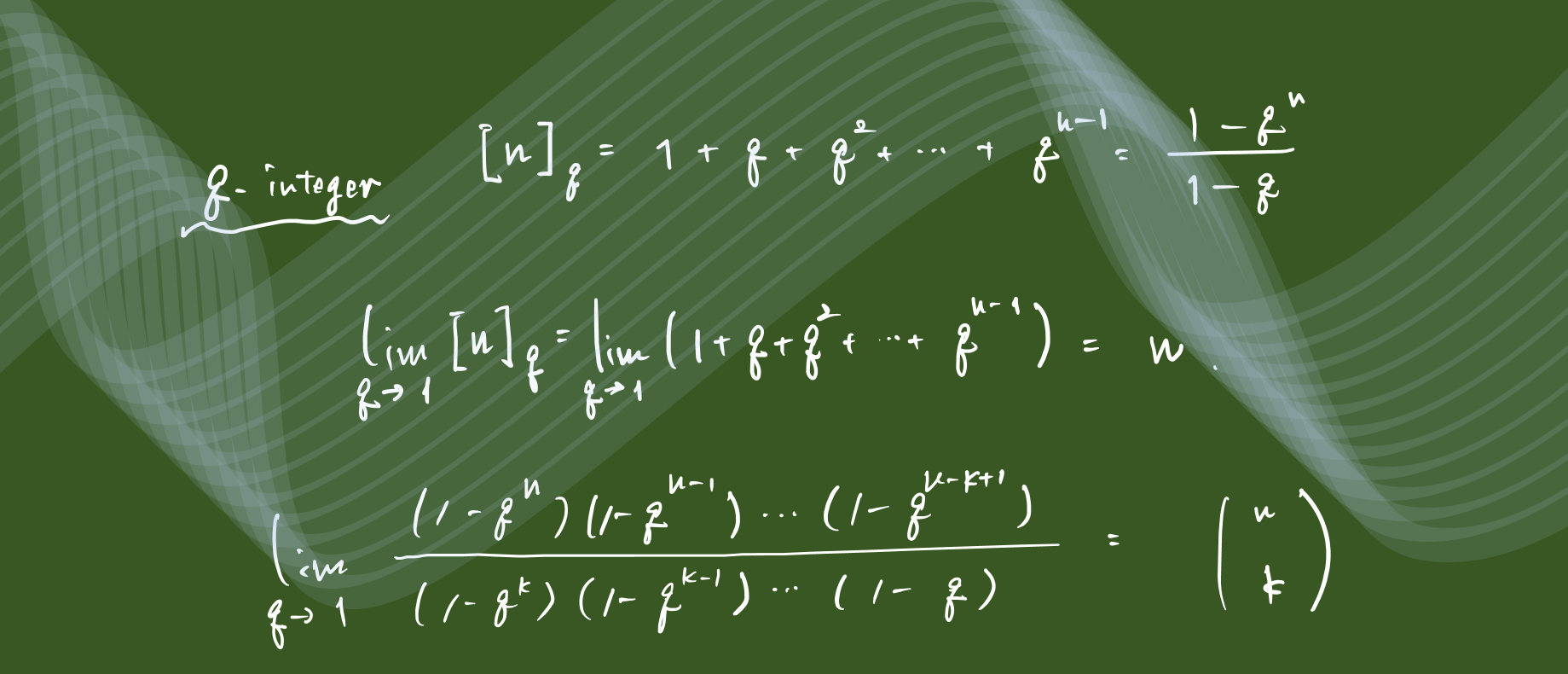
動画で見たい方はこちら↓↓↓

こんにちは。和からの数学講師の岡本です。かなり個人的な話ですが、最近二項定理をよくお見掛けするので、今回は変わった角度から二項定理を証明していこうと思います。
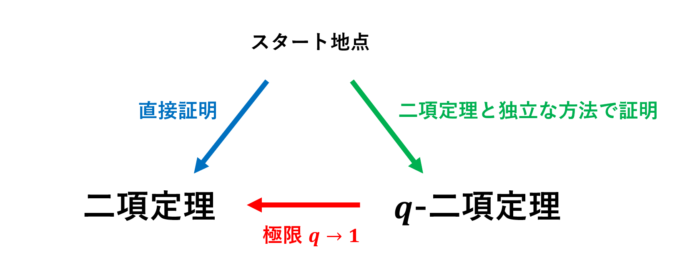
今回のメインは「$q$-二項定理」という、「二項定理」の一般化です。一般化したものを使ってもとのものを証明するなんて、天下りにもほどがあるように思えます。しかし、二項係数を経由せずに「$q$-二項定理」を証明できれば、この話にも大いに意味があるように思います。

１．そもそも二項定理とは

今回証明したい「二項定理」とは、以下の公式のことを指します。

$$\begin{align*} (1+x)^n=\sum_{k=0}^n\binom{n}{k}x^k. \end{align*}$$

ここで$\binom{n}{k}=\frac{n!}{k!(n-k)!}$であり、二項係数と呼ばれるものです。
例えば、$n=3$のとき

$$\begin{align*} (1+x)^3=1+3x+3x^2+x^3 \end{align*}$$

となります。この定理の直接的な証明やテイラー展開を使った証明は以前マスログで紹介されていますのでこちらをご覧ください。

テキストに載っていない二項定理の証明

２．$q$-変形と$q$-整数

世の中には何でも「変形」したいと思う人類がいます（僕です）。たとえば、パラメータ$q$を使って、関数や整数などを「変形」することを考えます。ただし、$q\to1$とすると元に戻るような変形でなくてはいけません。また、今後、収束の関係もあるので、このパラメータは$|q|<1$とします（複素数でも実数でもＯＫ）。 たとえば、2次関数$f(x)=x^2$の$q$-変形として$f_q(x):=qx^2$を考えてみます。たしかに$q\to 1$とすると元の$x^2$に戻るので、これは条件を満たした$q$-変形と言えます。では次に整数の「３」を変形してみましょう。たとえば、$3q$とか$3q^2$とかもアリですが、あまり「面白く」ありません。数ある$q$-変形でも、それなりに理論として「面白い」ものは存在します。それが、次のような変形です。

$$\begin{align*} [3]_q=1+q+q^2. \end{align*}$$

これもたしかに$q\to 1$とすると3になります。なお、自然数$n$に対して同様に定義した、

$$\begin{align*} [n]_q:=1+q+q^2+\cdots+ q^{n-1}=\frac{1-q^n}{1-q} \end{align*}$$

を、$q$-整数といいます。これは、格別な性質をもつ$q$-変形になっており、岡本の主観全開ですが、かなり好きです。

３．$q$-二項定理とは

実は二項定理にも$q$-変形バージョンが存在します。元の形が$(1+x)^n$だったところを

$$\begin{align*} (1+x)(1+qx)(1+q^2x)\cdots(1+q^{n-1}x) \end{align*}$$

とします。たしかに$q\to 1$で元の形に戻ります。この式の展開公式を$q$-二項定理と呼びます。実際に$n=3$の場合、

$$\begin{align*} (1+x)(1+qx)(1+q^2x)&=1+(1+q+q^2)x+(q+q^2+q^3)x^2+q^3x^3\\ &=1+[3]_qx+q[3]_qx^2+q^3x^3 \end{align*}$$

となり、なんと$q$-整数が現れます！このように互換性がある$q$-変形というのが理論上重要となってきます。
それでは、$q$-二項定理（展開公式）を述べましょう。

$x^k$の係数は、分母分子を$(1-q)^k$で割って整理すると

$$\begin{align*} \frac{(1-q^n)(1-q^{n-1})\cdots (1-q^{n-k+1})}{(1-q^k)(1-q^{k-1})\cdots(1-q)}q^{\frac{1}{2}k(k-1)}=\frac{[n]_q[n-1]_q\cdots[n-k+1]_q}{[k]_q[k-1]_q\cdots[1]_q}q^{\frac{1}{2}k(k-1)} \end{align*}$$

と計算でき、極限$q\to 1$を考えることにより、$\frac{n(n-1)\cdots(n-k+1)}{k(k-1)\cdots 1}=\binom{n}{k}$となります。したがって、$q$-二項定理に対して極限$q\to 1$により、通常の二項定理を得ることができました！このような変形を用いた計算を巷では「$q$-解析」と呼びます。また極限$q\to1$は俗に「古典化」といいます。うまく古典化ができ、全体として整合性があるような$q$-変形が岡本は大好きです。

４．さいごに

いかがでしたでしょうか？今回は$q$-二項定理の証明に踏み込んでいませんので、「天下り」感が否めません。そこで、次回は$q$-二項定理の証明を行おうと思います。実はこの定理は二項係数やその他の組み合わせ論的な手法を使わずに証明できますので、このあたりを詳しくまとめようと思います。次回もお楽しみに！

和からではオンラインによる集団授業や個別授業も行っております。算数から数学、統計学まで幅広く対応していますので、興味のある方はまずは無料の個別カウンセリングへ！

和からの数学教室

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>