\(q\)-二項定理の証明

ロマンティック

公開日

2021年11月17日

更新日

2021年11月17日

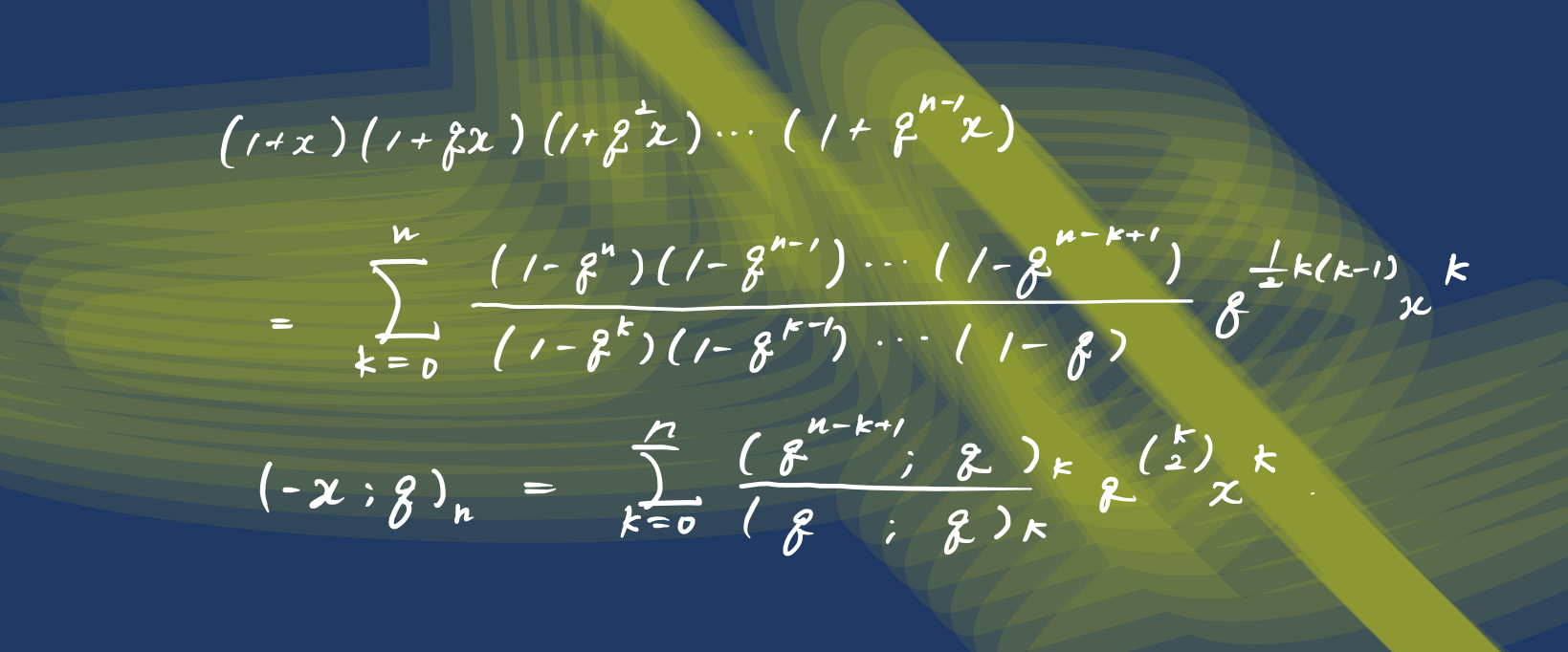
こんにちは。和からの数学講師の岡本です。前回は\(q\)-二項定理を使った二項定理の天下り的な証明をご紹介しました。

「(q)-二項定理」を使って「二項定理」を証明する

今回は「\(q\)-二項定理の証明」を解説していきたいと思います。

この記事の主な内容

１．\(q\)-二項定理とは

まずは復習として\(q\)-二項定理の主張を記しておきます。

(\(q\)-二項定理)
\begin{align*}
(1+x)(1+qx)\cdots(1+q^{n-1}x)=\sum_{k=0}^n\frac{(1-q^{n})(1-q^{n-1})\cdots (1-q^{n-k+1})}{(1-q^k)(1-q^{k-1})\cdots(1-q)}q^{\frac{1}{2}k(k-1)}x^k
\end{align*}

パラメータ\(q\)は\(|q|<1\)としておきましょう。そして、\(q\to1\)という極限を考えることで、上の等式は

\begin{align*}
(1+x)^n=\sum_{k=0}^n\binom{n}{k}x^k
\end{align*}

となり、二項定理が得られます。つまり、\(q\)-二項定理とは、二項定理の一般化（\(q\)-変形）と考えることができます。

２．オイラーの計算

\(q\)-二項定理の証明に入る前に、天才数学者レオンハルト・オイラーの計算をご紹介します。オイラーが計算した以下のような無限積の計算が\(q\)-二項定理証明のカギになっています。

\begin{align*}
f(x):=\prod_{n=0}^{\infty}\frac{1-q^nax}{1-q^nx}=\frac{(1-ax)(1-qax)(1-q^2ax)\cdots}{(1-x)(1-qx)(1-q^2x)\cdots}.
\end{align*}

この関数\(f(x)\)を展開したときの\(x^n\)の係数を\(A_n\)とします。つまり

\begin{align*}
f(x)=A_0+A_1x+A_2x^2+A_3x^3+\cdots
\end{align*}

この係数\(A_n\)を求めてみましょう。まず、\(A_0=1\)なのは積の形からすぐに分かります。また、\(f(x)\)の定義により

\begin{align*}
f(x)=\frac{1-ax}{1-x}f(qx)\Longleftrightarrow (1-x)f(x)=(1-ax)f(qx)
\end{align*}

であることがわかります。これにより、右辺と左辺の係数比較を行うことにより

\begin{align*}
A_k=\frac{1-q^{k-1}a}{1-q^k}A_{k-1}=\cdots=\frac{(1-a)(1-qa)\cdots(1-q^{k-1}a)}{(1-q^k)(1-q^{k-1})\cdots(1-q)}
\end{align*}

となり、これにより

\begin{align*}
f(x)=\sum_{k=0}^{\infty}\frac{(1-a)(1-qa)\cdots(1-q^{k-1}a)}{(1-q^k)(1-q^{k-1})\cdots(1-q)}x^k
\end{align*}

が得られました。

３．\(q\)-二項定理の証明

それではいよいよ\(q\)-二項定理の証明に入ります。まず、先ほどの関数\(f(x)\)に対して、\(x\)を\(-x/a\)と置き換えます。

\begin{align*}
\frac{(1+x)(1+qx)(1+q^2x)\cdots}{(1+x/a)(1+qx/a)(1+q^2x/a)\cdots}=\sum_{k=0}^{\infty}\frac{(1-a)(1-qa)\cdots(1-q^{k-1}a)}{(1-q^k)(1-q^{k-1})\cdots(1-q)}(-x/a)^k
\end{align*}

次に、\(a\)を\(q^{-n}\)に置き換えます。すると

\begin{align*}
\frac{(1+x)(1+qx)(1+q^2x)\cdots}{(1+q^nx)(1+q^{n+1}x)(1+q^{n+2}x)\cdots}=\sum_{k=0}^{\infty}\frac{(1-q^{-n})(1-q^{-n+1})\cdots(1-q^{-n+k-1})}{(1-q^k)(1-q^{k-1})\cdots(1-q)}x^k(-1)^kq^{nk}
\end{align*}

となり、左辺の無限積は分母が約分により消え、有限積になります。同時に右辺も\(x^{n+1}\)以降の係数が\(0\)になることから有限和になります（\(k>n\)のとき、係数の分母に\((1-q^0)\)が現れるため）。

\begin{align*}
(1+x)(1+qx)(1+q^2x)\cdots(1+q^{n-1}x)&=\sum_{k=0}^{n}\frac{(q^n-1)(q^{n-1}-1)\cdots(q^{n-k+1}-1)}{(1-q^k)(1-q^{k-1})\cdots(1-q)}q^{1+2+\cdots+(k-1)}x^k(-1)^k\\
&=\sum_{k=0}^{n}\frac{(1-q^n)(1-q^{n-1})\cdots(1-q^{n-k+1})}{(1-q^k)(1-q^{k-1})\cdots(1-q)}q^{\frac{1}{2}k(k-1)}x^k
\end{align*}

したがって、\(q\)-二項定理が証明できました！

４．さいごに

いかがでしたでしょうか？前回は「二項定理」を証明するために一般化である「\(q\)-二項定理」を用いて証明しました。しかし、今回ご紹介したように二項定理を直接経由せずに\(q\)-二項定理を証明することができます。このように、【「Ａ」を証明するのに「Ａ」の一般化である「Ａ’」を利用すること】はなんだか変な感覚かもしれませんが、数学ではしばしば起こります。「一般化」や「抽象化」することで初めて気づくことや、他分野とつながることは数学の研究、学習において非常に重要であると考えられますし、これは数学だけの話ではないと個人的には思っています。ものごとを１つ、２つ上に一般化して捉え、考えていくことは日常生活でも大切です。

今回の参考文献はこちらです。オイラーの無限解析に関するお話や、バーゼル問題、\(q\)-二項定理や分割数など、おもしろい話題が詰まっています！

オイラーに学ぶ―『無限解析序説』への誘い野海正俊(著) 日本評論社