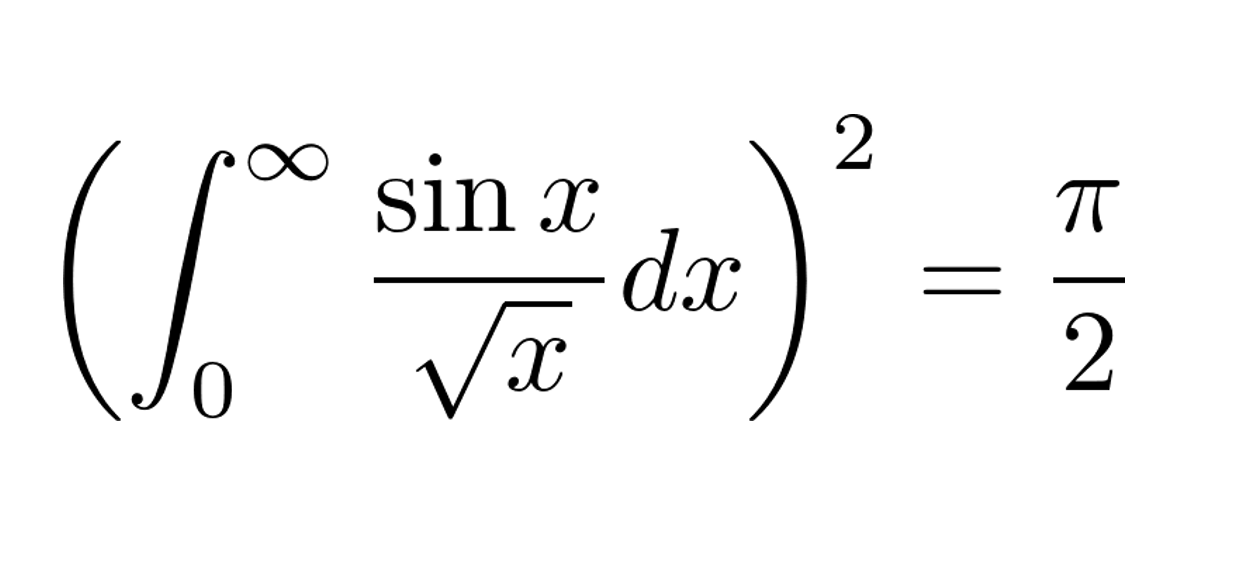
数学教室和(なごみ)講師の松中です。

本記事は、やばそうな数式の第4回の記事です。第1回の「意味編」、第2回の「総乗の証明編」、第3回の「総和の証明編」は以下のリンクからお読みください。本記事がやばそうな数式シリーズの完結編となります。

やばそうな数式(意味編)～キラキラ数学プロジェクト～

やばそうな数式(総乗の証明編)～キラキラ数学プロジェクト～

やばそうな数式(総和の証明編)～キラキラ数学プロジェクト～

今回は、やばそうな数式の積分の証明を行います。
$$\begin{align*} \left( \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx \right)^2 &=\frac{\pi}{2} \end{align*}$$

これはつまり、
$$\begin{align*} \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx &=\sqrt{\frac{\pi}{2}} \end{align*}$$
を証明すればよいことになります。左辺の積分が負にならないのは「意味編」でお見せしたグラフの面積と考えれば明らかでしょう。

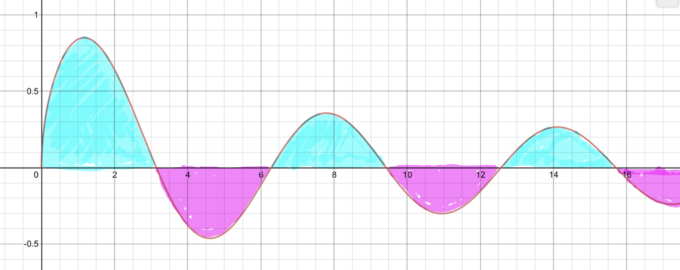
この積分は$\frac{\sin x}{\sqrt{x}}$という実数の関数の、実数の積分区間での積分(広義積分)となっていますが、この値を求める際に、複素数の関数である複素関数の積分が活躍します。実際、複素関数論を築き上げた数学者の一人であるコーシーは、複素関数の定積分への応用を重要視していました。実数関数の範囲でも証明はできると思いますが、本記事では複素関数を用いた証明を紹介します。ということで本証明を理解するために必要なレベルは、これまで紹介した数式の中で一番高い大学二年(複素関数)レベルとなっております。

証明

積分の書き換え

まずは$\sqrt{x}=t$という変数変換を行い積分をより簡単な形に書き換えます。

$$\begin{align*} \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx=2\int_{0}^{\infty} \sin {t^2}dt \end{align*}$$

ちなみに、この右辺の積分はフレネル積分という名前がついており、マスログで過去に紹介したクロソイド曲線のパラメータ表示にも表れる興味深い積分です。

高速道路の美しい曲線―安全運転のための数学―

ここで$e^{it^2}=\cos{t^2}+i\sin{t^2}$から、
$$\begin{align*} \int_{0}^{\infty} \sin {t^2}dt = {\rm Im}\int_{0}^{\infty} e^{it^2} dt \end{align*}$$

となるので、以下の積分の値を求めればよいことが分かります。
$$\int_{0}^{\infty} e^{it^2} dt$$

今回は複素関数を用いて証明するので、被積分関数の変数を$t$から$z$に変え、$f(z)$と名前を付けておきます。
$$f(z)=e^{iz^2}$$

積分路に沿った複素積分

先の積分の値を求めるために、$R$を正の実定数として以下の閉曲線$C=C_1+C_2+C_3$に沿って$f(z)$を積分してみます。

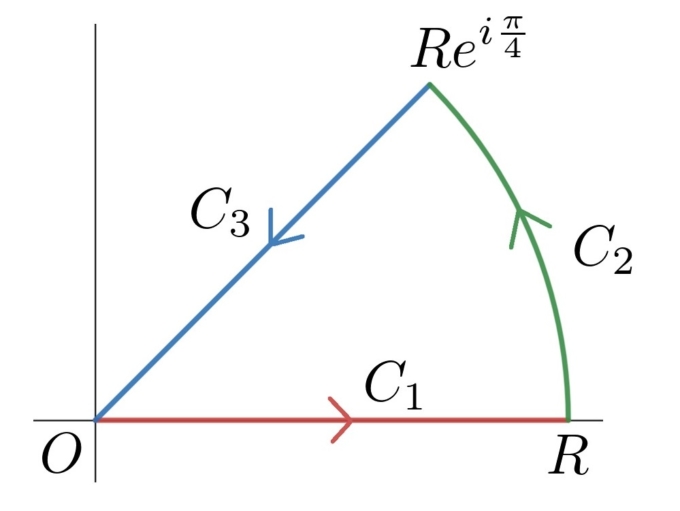
$$\int_C f(z)dz=\int_{C_1} f(z)dz+\int_{C_2} f(z)dz+\int_{C_3} f(z)dz$$

ここで、$f(z)$は${\mathbb C}$上で正則ですから、コーシーの積分定理から、

$$\int_C f(z)dz=0$$
が成り立つので、
$$\int_{C_1} f(z)dz+\int_{C_2} f(z)dz+\int_{C_3} f(z)dz=0$$
となります。さらに$R\rightarrow \infty$とすることで、
$$\lim_{R\rightarrow \infty}\int_{C_1} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_3} f(z)dz=0$$
とできるので、この3つの項を順に計算していきます。

$C_1$に沿っての積分

$C_1$上の積分は$C_1$を$z=t\,(0\leq t\leq R)$とパラメータ表示することで、

$$\int_{C_1} f(z)dz=\int_0^R e^{it^2}dz$$
と変形できます。
この積分で$R\rightarrow \infty$とすることで、求めたい積分が現れます。

$$\lim_{R\rightarrow \infty}\int_{C_1} f(z)dz=\int_0^\infty e^{it^2}dz$$

よって、$\displaystyle\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz$と$\displaystyle\lim_{R\rightarrow \infty}\int_{C_3} f(z)dz$の値が分かれば、

$$\lim_{R\rightarrow \infty}\int_{C_1} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_3} f(z)dz=0$$
から、
$$\int_0^\infty e^{it^2}dz$$
の値を求めることができます。

$C_2$に沿っての積分

$C_2$上の積分は$C_2$を$z=Re^{it}\,(0\leq t\leq \frac{\pi}{4})$とパラメータ表示することで、$dz=Rie^{it}dt$より、

$$\int_{C_2} f(z)dz=\int_0^{\frac{\pi}{4}} e^{iR^2e^{2it}}Rie^{it}dt$$

となります。ここで$\displaystyle\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz=0$を証明するために、まずは被積分関数の絶対値を求めておきます。

$$\left|e^{iR^2e^{2it}}Rie^{it}\right|=R\left|e^{iR^2(\cos{2t}+i\sin{2t})}\right|=Re^{-R^2\sin{2t}}$$

これから、
$$\left|\int_{C_2} f(z)dz\right|=\left|\int_0^{\frac{\pi}{4}} e^{iR^2e^{2it}}Rie^{it}dt\right|\\\\ \leq \int_0^{\frac{\pi}{4}}\left|e^{iR^2e^{2it}}Rie^{it}\right|dt \leq R\int_0^{\frac{\pi}{4}}e^{-R^2\sin{2t}}dt\\\\ \leq R\int_0^{\frac{\pi}{4}}e^{-R^2\frac{4}{\pi}t}dt=R\left[-\frac{\pi}{4R^2}e^{-R^2\frac{4}{\pi}t}\right]_0^{\frac{\pi}{4}}\\\\ =\frac{\pi}{4R}\left(1-e^{-R^2}\right)$$
となります。上の式変形では、$e^{-R^2\sin{2t}}\leq e^{-R^2\frac{4}{\pi}t}$を用いてます。この事実は、$0\leq t\leq\frac{\pi}{4}$で、$\sin{2t}\geq\frac{4}{\pi}t$であることからわかります。

よって
$$\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz=\lim_{R\rightarrow \infty}\frac{\pi}{4R}\left(1-e^{-R^2}\right)=0$$
が成り立ちます。

$C_3$に沿っての積分

$C_3$上の積分は$C_3$を$z=(R-t)e^{i\frac{\pi}{4}}\,(0\leq t\leq R)$とパラメータ表示することで、$dz=-e^{i\frac{\pi}{4}}dt$より、

$$\int_{C_3} f(z)dz=\int_0^R e^{i(R-t)^2e^{i\frac{\pi}{2}}}(-e^{i\frac{\pi}{4}})dt=-e^{i\frac{\pi}{4}}\int_0^R e^{-(R-t)^2}dt$$

次に$s=R-t$と変数変換をすると、

$$-e^{i\frac{\pi}{4}}\int_0^R e^{-(R-t)^2}dt=-e^{i\frac{\pi}{4}}\int_0^R e^{-s^2}ds$$

となります。

ここで、$R\rightarrow \infty$とすると、
$$\lim_{R\rightarrow \infty}\int_0^R e^{-s^2}ds=\int_0^\infty e^{-s^2}ds$$
となりますが、これはガウス積分と呼ばれる有名な積分でこの値は、$\displaystyle \frac{\sqrt{\pi}}{2}$となります。

以上まとめて、
$$\lim_{R\rightarrow \infty}\int_{C_3} f(z)dz=-e^{i\frac{\pi}{4}}\frac{\sqrt{\pi}}{2}$$

がわかります。

各積分値の統合

以上の結果を
$$\lim_{R\rightarrow \infty}\int_{C_1} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_2} f(z)dz+\lim_{R\rightarrow \infty}\int_{C_3} f(z)dz=0$$
に代入すると、
$$\int_0^\infty e^{it^2}dz+0-e^{i\frac{\pi}{4}}\frac{\sqrt{\pi}}{2}=0$$
から、
$$\int_0^\infty e^{it^2}dz=e^{i\frac{\pi}{4}}\frac{\sqrt{\pi}}{2}=\frac{\sqrt{\pi}}{2}\left(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)$$
がわかります。

よって目的としていた積分の値が以下のように計算できます。

$$\begin{align*} \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx&=2\int_{0}^{\infty} \sin {t^2}dt\\\\ &=2 {\rm Im}\int_{0}^{\infty} e^{it^2} dt=2{\rm Im}\left(\frac{\sqrt{\pi}}{2}\left(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)\right)\\\\ &=\sqrt{\frac{\pi}{2}} \end{align*}$$

まとめ

今回はやばそうな数式シリーズの最終回として積分の等式を証明しました。なかなか長く大変な証明でしたが、無事完結しました。数学の世界には小学生や中学生でも意味は分かるものの、その証明には大学レベルの数学を要するものが少なくなく、やばそうな数式もそのような例でした。今回の証明を難しいと感じた方も一歩一歩勉強していけばきっと理解できるはずです。興味を持った方は複素関数の勉強をしてみてください！

<文/松中>

■本記事を理解するためのおすすめ個別講座

複素関数論