和からの松中です。今年も日曜数学のアドベントカレンダーに投稿させていただきます！昨年のテーマは「偏角の原理を使って五次方程式を解く」でしたが、今年は偏角の原理を使ってゼータ関数の零点を見つけてみようと思います！これはつまりあの有名なリーマン予想にチャレンジしてみようということです。

本記事の内容を動画で見たい方はこちら↓↓↓

偏角の原理を使って五次方程式を解く

リーマン予想とは

リーマン予想とはドイツの天才数学者リーマンが1859年に発表し、160年以上経っている今日でも未解決の数学の予想です。リーマン予想はミレニアム懸賞金問題の一つであり、この予想を証明する、もしくは反例を挙げることで懸賞金1億円が手に入るという夢のような予想になっています。

リーマン予想の主役はゼータ関数とその零点です、まずゼータ関数とは以下で定義される関数を複素平面全体に有理型接続したものなのですが、本記事では複素数を入れたら複素数が出てくる関数ということだけわかっていただければよいかと思います。

\[
\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}\,\,\,\,({\mathrm Re}(s)>1)
\]

そして、ゼータ関数の零点というのはゼータ関数の出力が\(0\)になる入力のことです。つまり次の式を満たす複素数\(\alpha\)をゼータ関数の零点と呼びます。

\[
\zeta(\alpha)=0
\]

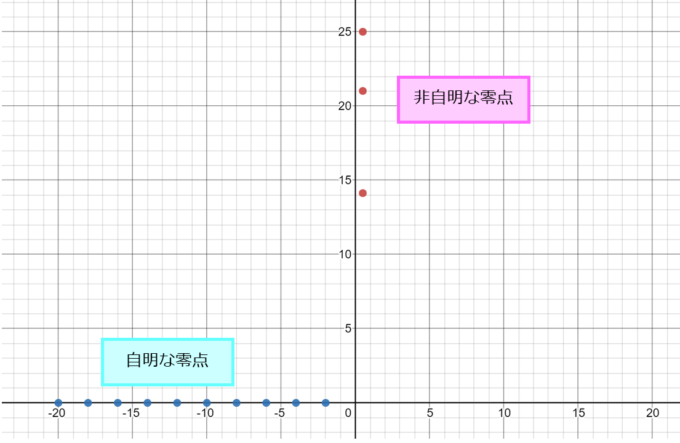
ゼータ関数の零点は「自明な零点」と「非自明な零点」の2グループに分かれます。「自明な零点」というのは\(-2\)、\(-4\)、\(-6\)などマイナスの偶数のことです。自明というのは比較的簡単に零点であるということがわかるという意味で、実はマイナスの偶数は全てゼータ関数の零点であることが知られています。
\[
\zeta(-2)=0,\,\,\,\zeta(-4)=0,\,\,\,\zeta(-6)=0,\cdots
\]

「自明な零点」でない零点のこと「非自明な零点」と呼び、リーマン予想はこの非自明な零点が複素平面上でどこに分布しているかを言及している予想になるのです。

リーマンがゼータ関数を研究していた当時、リーマンは実際に非自明な零点を計算で求めていたそうです。そしてリーマンはある事実に気づきます。

「自分が見つけた非自明な零点の実部は全て\(\frac{1}{2}\)だった、、まさか非自明な零点の実部は全て\(\frac{1}{2}\)なのでは！！？」

これがリーマン予想の始まりです。

ところで、なぜ非自明な零点が重要なのでしょうか？それは非自明な零点の情報によって原理的には全ての素数の位置を知ることができるからです。素数は古代から数学者の心を魅了してきた魅惑の数たちです。リーマン予想は素数の分布に関する重要な予想なのです。

リーマン予想、ゼータ関数、素数については様々な記事が公開されているので興味を持った方は是非調べてみてください！

偏角の原理を用いて零点探し

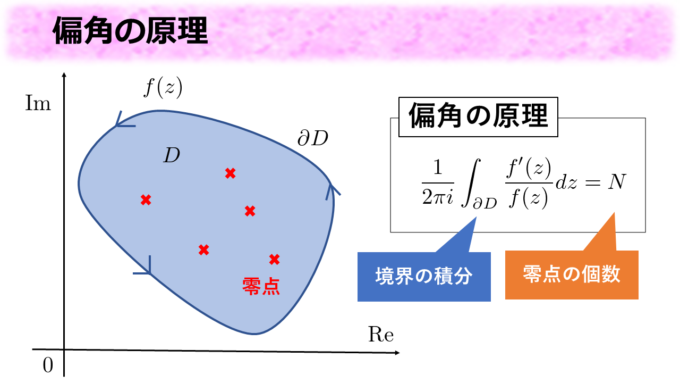
偏角の原理については昨年の記事で紹介させていただきました。簡単に言うと複素関数\(f(z)\)から得られる関数\(\frac{1}{2\pi i}\frac{f^{\prime}(z)}{f(z)}\)を単純閉曲線に沿って積分することで、その閉曲線の中にある\(f(z)\)の零点の個数がわかるというものです。もう少し詳しく知りたい方はぜひ昨年の記事をお読みください。そしてもっとしっかり詳しく知りたいという方は大学数学の複素関数の勉強をしてみてください。

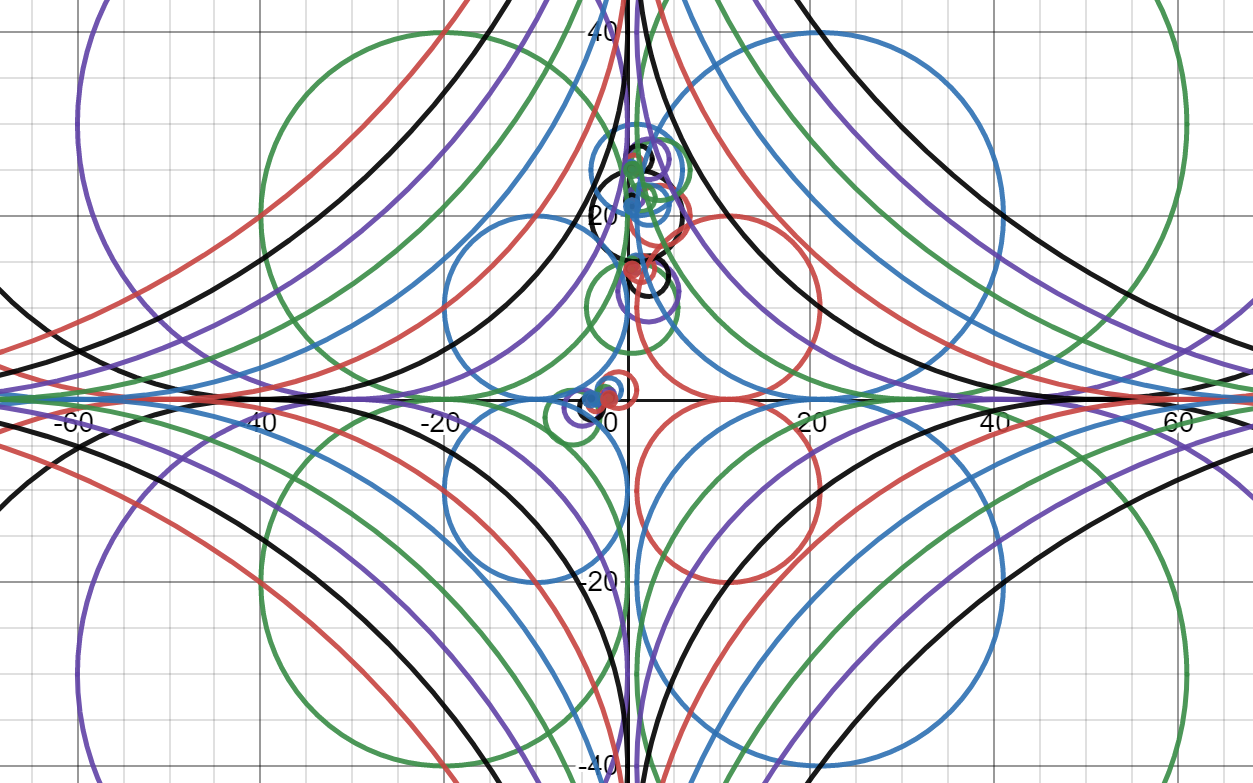
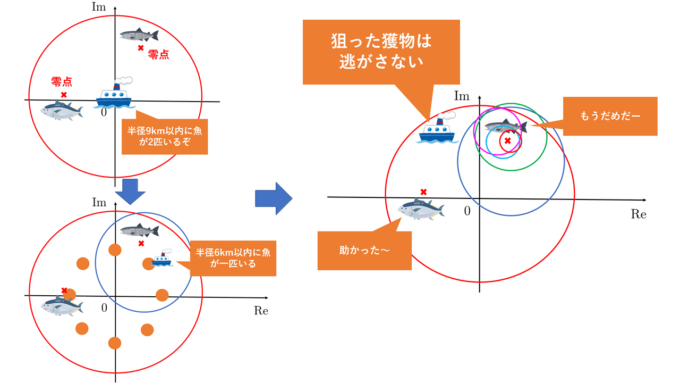
偏角の原理を用いることで、複素平面上に描いた円の中に何個の零点があるかがわかります。1つでも零点があることがわかれば、より小さい円で元の円を覆っていくことによって、零点の位置をより狭い範囲に絞ることができます。これを繰り返すことで零点の位置を求めることができるのです。

さて、昨年はこの\(f(z)\)として五次多項式を選ぶことで、代数的な解の公式がないとされる五次方程式の複素数解を見事に求めることができました(厳密解ではなく数値解ですが)。本記事ではこの\(f(z)\)として\(\zeta(s)\)関数を選んで、零点を見つけてみましょう！

自明な零点\(s=-2\)

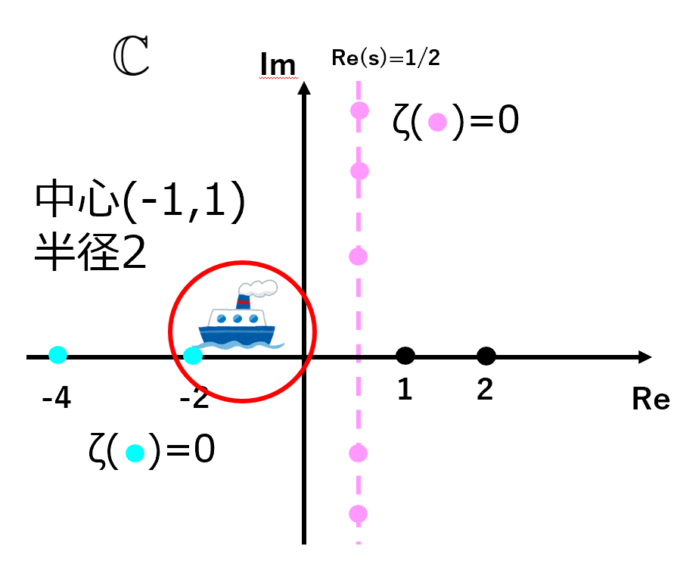
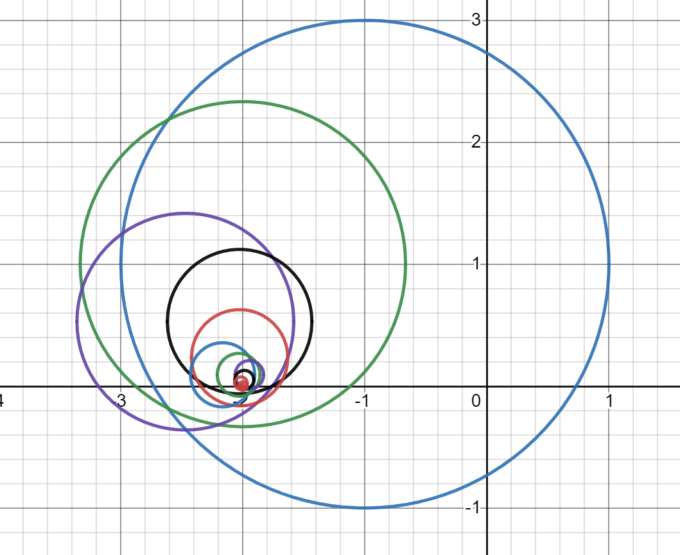
偏角の原理を用いて零点を探す際、最終的にどの零点に行きつくかは、最初の円の選び方に依ります。まずは自明な零点\(s=-2\)に行きつくために、恣意的ですが最初の円を中心\((-1,1)\)、半径\(2\)として零点を探してみます。

結果、以下のように確かに\(s=-2\)を捕らえることができました。

自明な零点\(s=-4\)

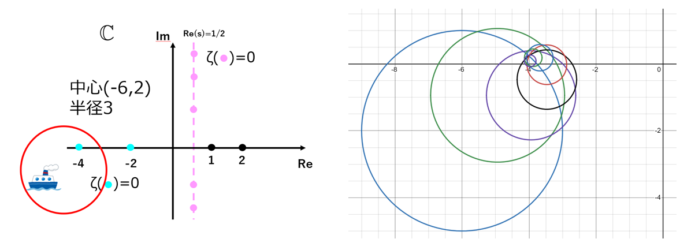
もう一つ自明な零点を求めてみましょう。今度も恣意的ですが、最初の円を中心\((-6,-2)\)、半径\(3\)として零点を探してみます。結果、こちらもしっかり自明な零点\(s=-4\)を捕らえることができました。

非自明な零点\(s=\frac{1}{2}+14.134\cdots i\)

現在見つかっている非自明な零点の実部はもちろん全て\(\frac{1}{2}\)です。虚部が正の範囲で一番小さい非自明な零点は\(s=\frac{1}{2}+14.134\cdots i\)となっています。これはリーマンも実際に求めていた零点です。

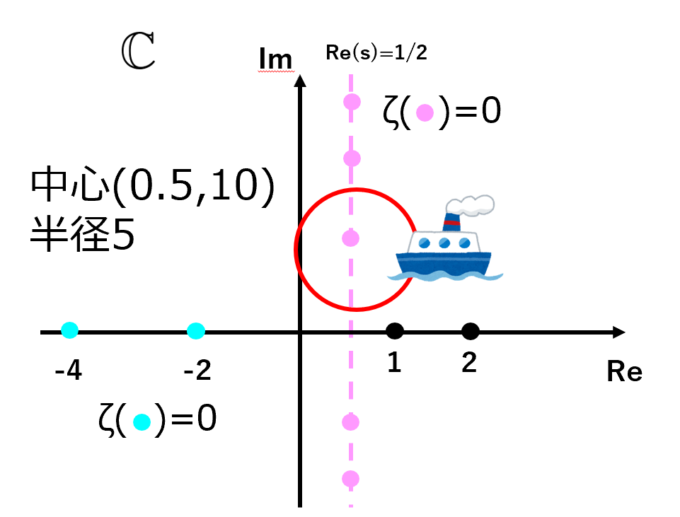
さて偏角の原理を用いた方法で非自明な零点をもとらえることができるのでしょうか！？これまで同様かなり恣意的な設定となりますが、最初の円の中心を\((0.5,10)\)、半径を\(5\)にして実験してみましょう！

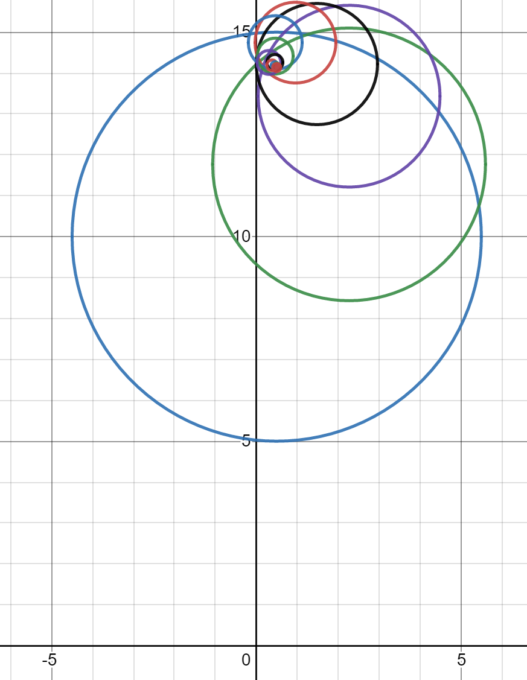
いよいよ結果発表です！結果は以下の通りです。

すごい！！非自明な零点をしっかりとらえているではありませんか！リンクを張るのでいかに執拗に非自明な零点を追い込んでいるかを確認してみてください。プログラムのパラメータを変えればもっと執拗にすることもできます。

1個目の非自明な零点が追い込まれていることが良くわかるリンク

非自明な零点\(s=\frac{1}{2}+21.022\cdots i\)

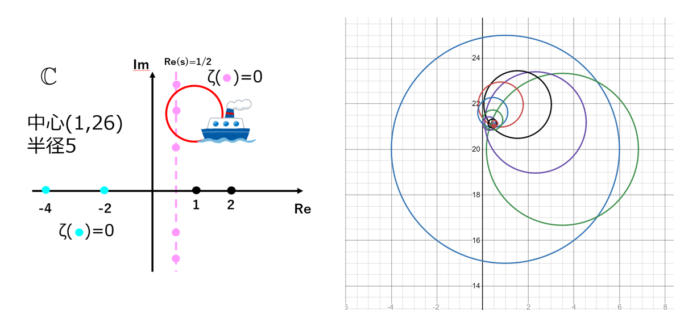
もちろん、次の非自明な零点も円の中心を\((1,26)\)、半径を\(5\)として始めることで簡単に仕留めることができます。

こちらもリンクを張っておくので、零点の気持ちになって円たちに追い詰められてみてください！

2個目の非自明な零点が追い込まれていることが良くわかるリンク

マウスや指でなぞって零点を追い詰めよう

さて、ここからが本題です。前節までで偏角の原理を用いて零点を求めることの有効性が確認できたと思います。しかし、個人的になにかが物足りません。それは以下の理由によるものではないかと思います。

　
とくに3点目は深刻です。心ときめいてこその数学、日曜数学です！

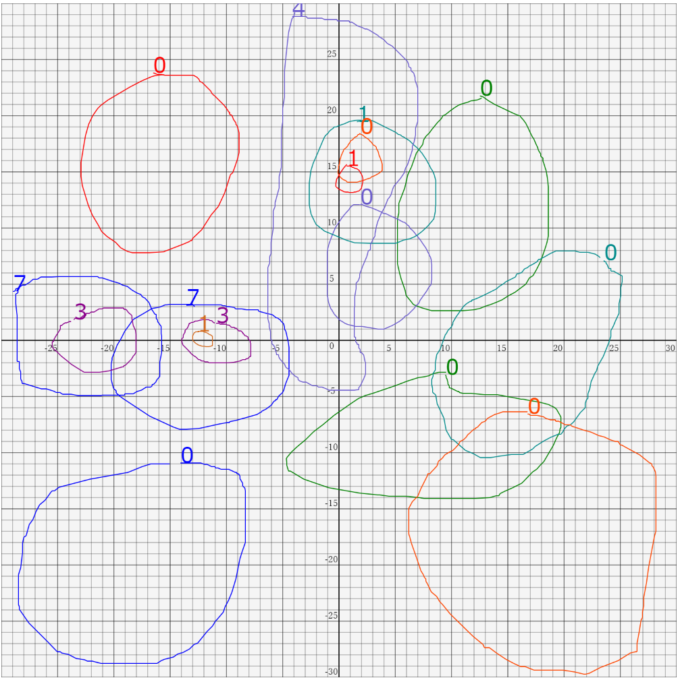
そこで心躍らせるために今年はもっと能動的に零点を探せるWEBアプリを開発しました！遊び方はシンプルです。ブラウザ上に表示される複素平面をマウスや指でなぞって閉曲線を描くと、変革の原理を使ってその中の零点の個数がわかります。その情報をもとに零点たちを追い込んでいきましょう！

■今回開発したアプリ
http://118.27.115.150/mattyuu/zero_searcher/
※一応スマホやタブレットでも遊べます。

「まずは大きめの閉曲線(包囲網)を描いて、ちょっとずつ零点たちを追い詰めていく」、「いきなりピンポイントに零点たちを攻める」など遊び方はたくさんあります。前節で紹介した閉曲線は全て綺麗な真円でしたが、閉曲線は円である必要はありません。自分なりの閉曲線で楽しんでください。

なお、こちらのアプリで遊ぶ際の注意事項は以下になります。

　
4点目は重要です。自分はすでにリーマン予想を知ってしまっています。そのため本当の意味で零点を追い詰めていくワクワクを味わうことができません。ゼータ関数の零点を全く知らない人がこのアプリでリーマン予想にたどり着いたとしたら、それはとても素敵なことだと思います。(すみません、この記事をここまで読んでくださった方には現在知られている非自明な零点の情報を伝えてしまいました。)

またリーマン予想を知っている方も、「なぜ時計回りに積分をしたら符号が変わるのか」、「なぜ\(1\)を囲ってしまうと零点の個数より\(1\)小さい値が表示されるのか」、「コンピュータプログラムはどうやって\(\zeta(s)\)や\(\zeta^{\prime}(s)\)を計算しているか」などなど奥深い話はいくらでもあるので、一緒に数学の世界を楽しみましょう。

明日は子葉さんの「リーマン予想と同値な等式や不等式」です！明日もリーマン予想です！

参考文献

ゼータ関数の零点計算の歴史や手法が詳しく載っている

ゼータ関数入門書としておすすめ

この記事の内容を深く知りたい方はこちらの講座がおすすめです。

リーマン予想入門

複素関数論

(文/松中)