幾何学の美しい性質～フェルマー点とは～

ロマンティック

公開日

2021年3月11日

更新日

2021年3月11日

こんにちは。和からの数学講師の岡本です。今回は「フェルマー点」と言われる、美しすぎる性質について紹介していきます。
幾何学の美しい話題として以前マスログに紹介した以下の記事も併せてご覧ください。

モーリーの奇跡

モーリーの定理の証明～三角比を使った方法～

この記事の主な内容

１．最短中継地点とフェルマー点

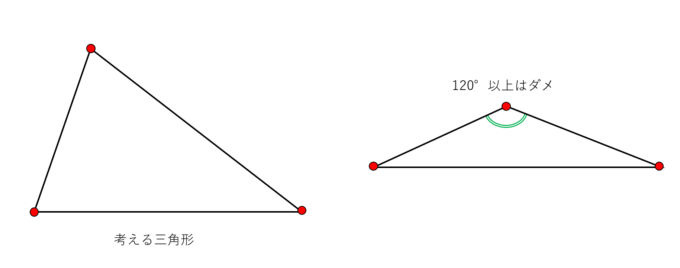
まず、野良の三角形を用意します。ただし、内角が120°を超えるような鈍すぎる三角形はダメです。この三角形に対して次のような問題を考えます。

【問題】
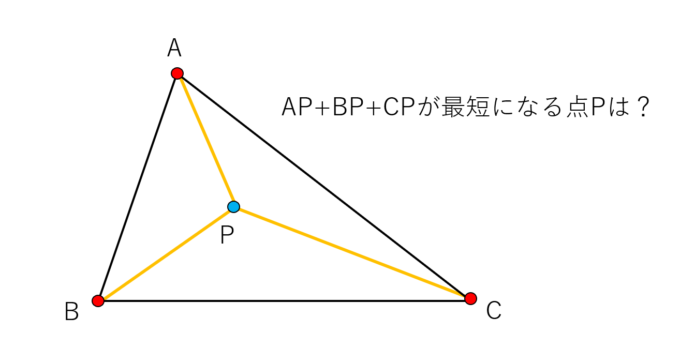
三角形ABCの内部の点で、各頂点からの距離の和AP+BP+CPが最小になるような点Pを見つけ出せ。

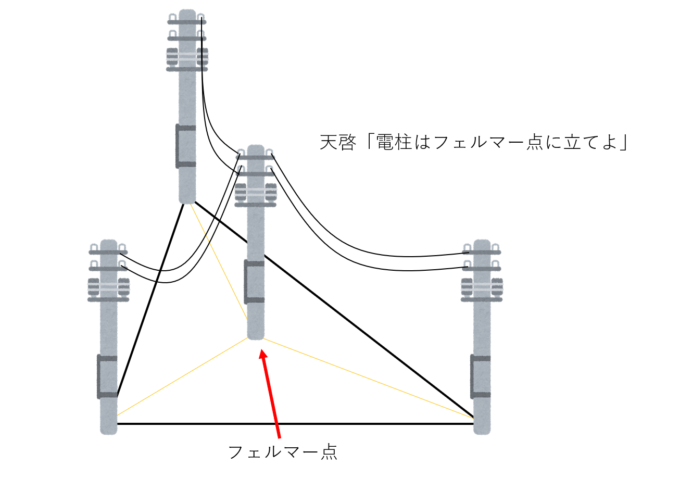
この問題は電信柱の設置場所などに応用できます。つまり、三角形の頂点を「地点」とし、各地点に最小コスト（最短の長さ）で電線をつなげるための中継地点をどこにすればいいかという問題に置き換えることができます。実はこの問題の答えとなる、点Pを三角形ABCのフェルマー点といいます。17世紀の数学大愛好家であるピエール・ド・フェルマーがこの問題を考察したことに由来します。

/p>

２．フェルマー点の性質

次に、このフェルマー点の驚くべき性質をご紹介します。

【性質】
三角形ABCの内部の点PがAP+BP+CPを最小にする点であるとするとき、点Pから各頂点に伸びる線のなす角は全て120°となる。

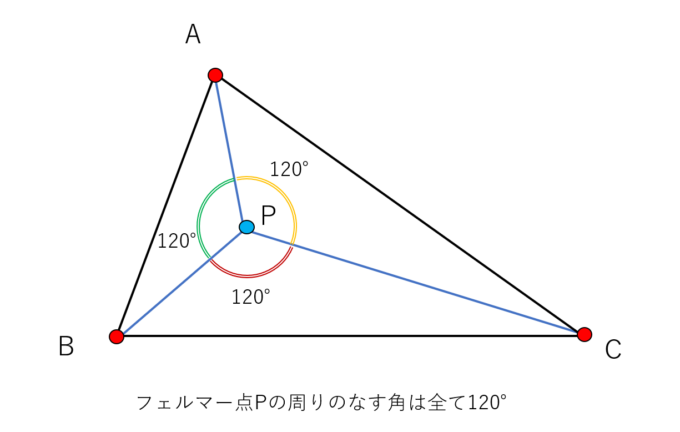
えーーーーーーーーー！！！！うそ！本当？？？？え、えーー！！という感じですよね。私も最初はそうなりました。そして本当に面白いのはこの性質の証明です。実際に証明していきます。

まず、与えられた三角形ABCと内部の点Pについて、頂点Aを中心にして線分AP, ACを反時計回りに60°回転させます。

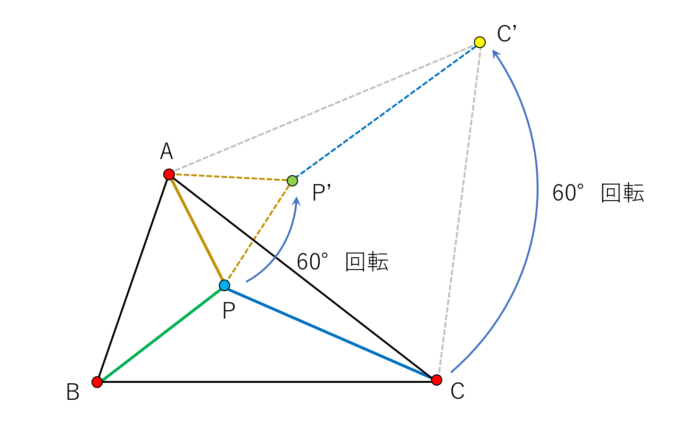
P, Cが回転してできた位置を上の図のようにそれぞれP’, C’とします。このときP’C’=PCであり、三角形APP’は正三角形であることからPP’=APであることがわかります。つまり、

\begin{align*}
AP+BP+CP=BP+AP+CP=BP+PP’+P’C’
\end{align*}

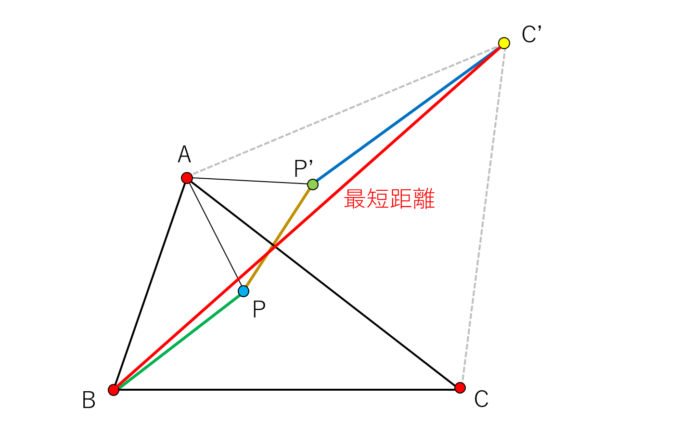
となり、この長さが最小になるため（＝点Pがフェルマー点となるため）には図のBC‘まで一直線上に並ぶことが必要十分条件になります。これにより、\(\angle\)BPA=180°-60°=120°、\(\angle\)APC=\(\angle\)AP’C’=180°-60°=120°となることがわかり、フェルマー点から各頂点への線のなす角は全て120°であることがわかります。

３．フェルマー点の見つけ方

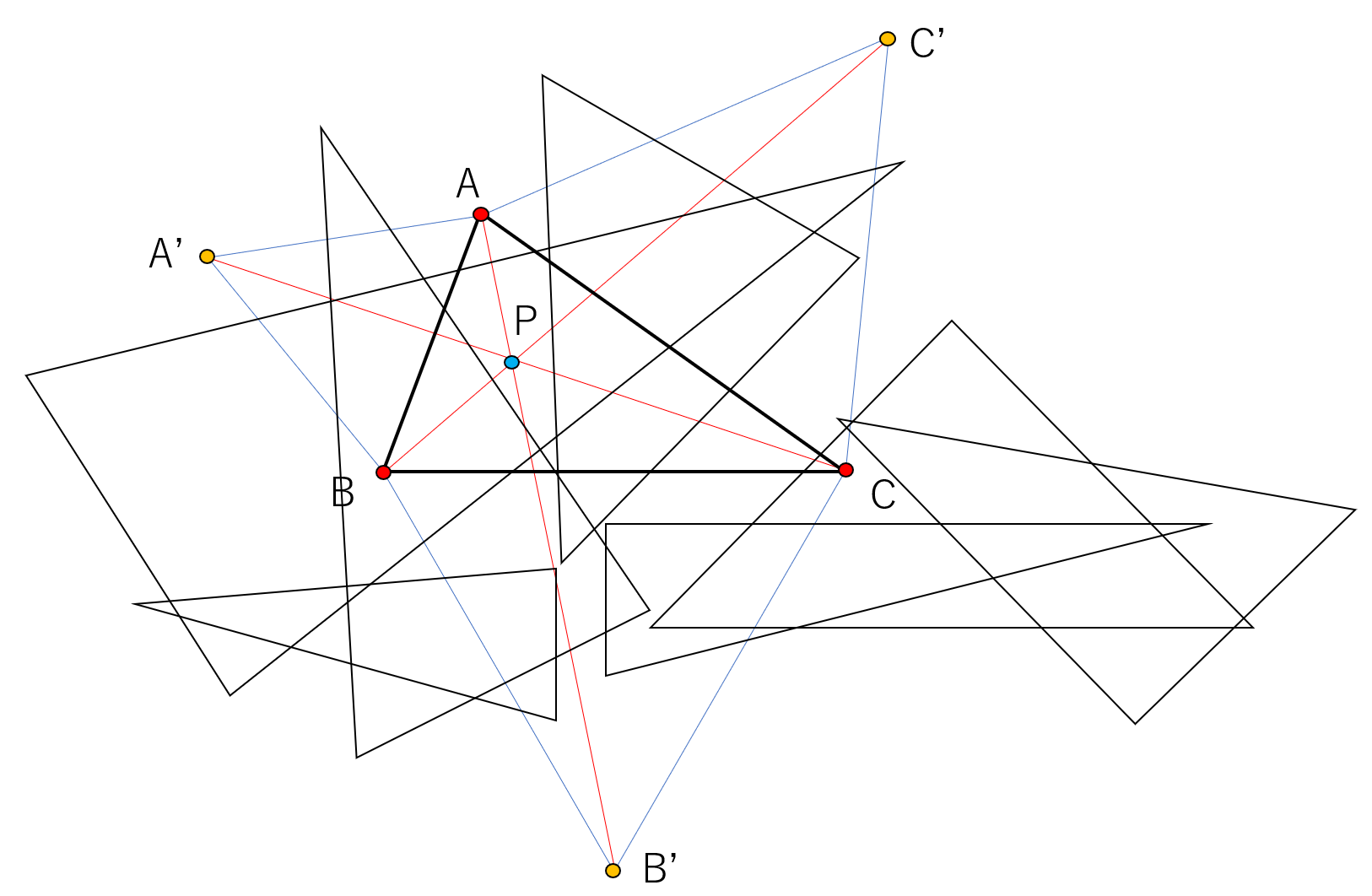
以上の考察を踏まえると、フェルマー点に探し方は簡単です。まず辺ACの長さの正三角形AC’Cと辺BCの長さの正三角形BB’Cを図のように設定します。

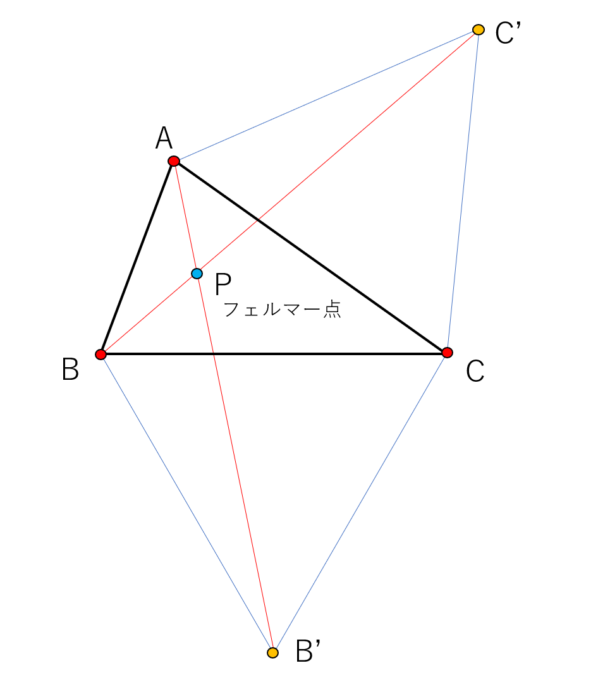
そして、直線BC’と直線AB’を描き、その交点をPとします。これが求めるフェルマー点となるわけです。

ちなみに、この現象はシャボン玉の膜でも見ることができます。実際に柱を立てて、シャボン玉溶液に浸すと、膜がフェルマー点で交わります。しかも柱が4本の場合でもうまく中継地点を2つ取って、結果的に膜のなす角が常に120°になるのです！つまりシャボン玉は最適なネットワークを自動的に構成してしまいます！すごいですよね！（これは、シャボン玉の膜が面積最小になるという性質から来ています。参考https://mathsoc.jp/publication/tushin/2201/2201koiso.pdf）面白いので時間がある方が是非試してみましょう！

４．さいごに

いかがでしたでしょうか。今回は所謂初等幾何学の話題でした。ちなみにこの話題は過去の東京大学の入試問題（2013年第4問）にも出題されており、知っていると瞬殺できる問題です。また今回の図の作成は主にパワーポイントのオブジェクトを利用しました。幾何学的な構造がわかっていると、パワーポイントで多様なデザインが可能になります。和からでは、数学的なデザインに関するセミナーを開催しております。気になった方は無料のセミナーに是非ご参加ください。