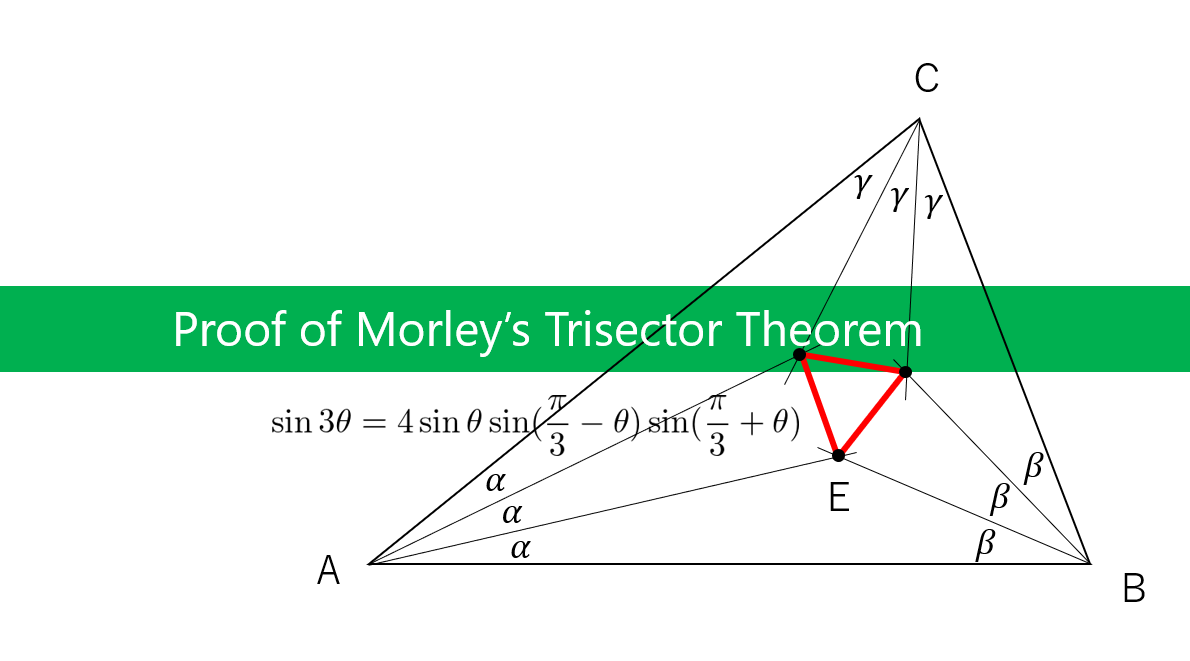
こんにちは。和からの数学講師の岡本です。以前、「モーリーの奇跡」というタイトルのマスログで紹介した「モーリーの定理」。今回はこの美しい定理の証明を簡単にまとめていこうと思います。

１．モーリーの定理

詳しくは以前のマスログをご覧ください

モーリーの奇跡

一応ここでも定理の主張を書いておきます。

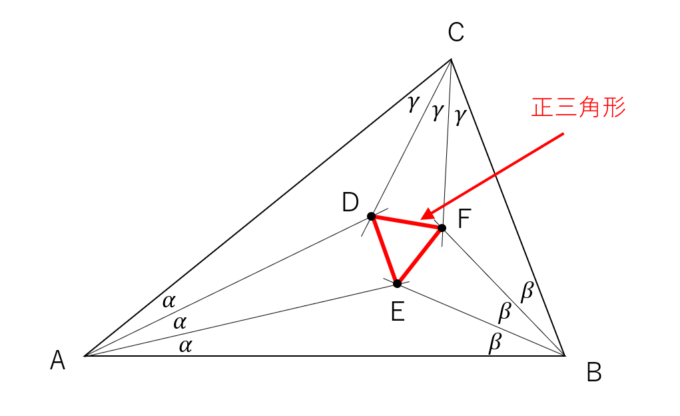
美しいですよね。。。適当な三角形から正三角形が構成できるわけですから！今回はこの定理をしっかり味わっていきます。

２．3倍角に関する補題

早速定理の証明に入っていきたいのですが、証明の際に鍵となる補題について、まずはまとめてみようと思います。

証明しましょう。まず、通常の$\sin$の3倍角の公式を使って変形していきます。

$$\begin{align*} \sin3\theta &=3\sin \theta-4\sin^3\theta\\ &=\sin\theta (3-4\sin^2\theta)\\ &=\sin \theta (3\cos^2\theta-\sin^2\theta)\\ &=\sin \theta (\sqrt{3}\cos\theta -\sin \theta)(\sqrt{3}\cos \theta+\sin \theta)\\ &=4\sin\theta\left(\frac{\sqrt{3}}{2}\cos \theta-\frac{1}{2}\sin\theta\right)\left(\frac{\sqrt{3}}{2}\cos +\frac{1}{2}\sin \theta\right)\\ &=4\sin \theta \sin\left(\frac{\pi}{3}-\theta\right)\sin \left(\frac{\pi}{3}+\theta\right) \end{align*}$$

というわけで、少し変わった3倍角の公式を示すことができました。これを使ってモーリーの定理の証明に入ります。

３．モーリーの定理の証明

証明で使う三角形の図を用意します。

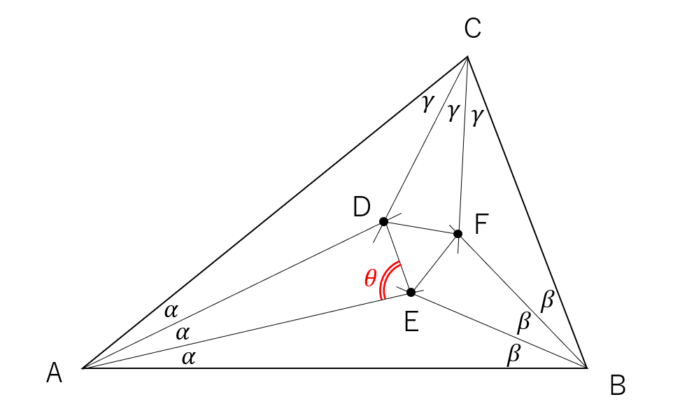
ひとまずの目標は上の図の角度$\theta$を求めることになります。これを求めるのに、正弦定理と$\sin$の3倍角公式を利用します。そのためにまず、三角形ABEに注目し、辺AEの長さを求めます。正弦定理より

$$\begin{align*} \frac{\text{AE}}{\sin \beta}=\frac{\text{AB}}{\sin (\pi-\alpha-\beta)}=\frac{\text{AB}}{\sin (\alpha+\beta)} \end{align*}$$

が成り立ちます。さらに、三角形ABCの外接円の半径を$R$とすることで

$$\begin{align*} \frac{\text{AB}}{\sin 3\gamma}=2R \end{align*}$$

が成り立ちます。これにより、辺AEは

$$\begin{align*} \text{AE}=\frac{2R\sin 3\gamma \sin \beta}{\sin(\alpha+\beta)}=\frac{2R\sin 3\gamma \sin \beta}{\sin\left(\frac{\pi}{3}-\gamma\right)} \end{align*}$$

と表現できます。ただし、最後の等式は三角形ABCの内角の和が$3\alpha+3\beta+3\gamma =\pi$であることを使いました。ここで補題の3倍角の公式を$\sin 3\gamma$に対して使います。すると

$$\begin{align*} \text{AE}&=\frac{8R\sin \gamma \sin \left(\frac{\pi}{3}-\gamma\right) \sin \left(\frac{\pi}{3}+\gamma\right)\sin \beta}{\sin\left(\frac{\pi}{3}-\gamma\right)}\\ &=8R\sin \gamma \sin \left(\frac{\pi}{3}+\gamma\right)\sin \beta \end{align*}$$

辺ADに対して同様の考察を行います。位置関係を考えると$\beta$と$\gamma$が入れ替わるだけです。

$$\begin{align*} \text{AD}=8R\sin \beta \sin \left(\frac{\pi}{3}+\beta\right)\sin \gamma \end{align*}$$

AEもADも$8R\sin \beta \sin \gamma$という部分が共通しています。したがって以下のような等式が成り立ちます。

$$\begin{align*} \frac{\text{AE}}{\sin \left(\frac{\pi}{3}+\gamma\right)}=\frac{\text{AD}}{\sin \left(\frac{\pi}{3}+\beta\right)} \end{align*}$$

正弦定理より、なんと$\theta=\frac{\pi}{3}+\beta, \theta’=\frac{\pi}{3}+\gamma$であることが確定します（まずこの角度が三角形AEDで矛盾なく設定でき、これ以外に角度の解がないことも簡単な考察から示せます）。

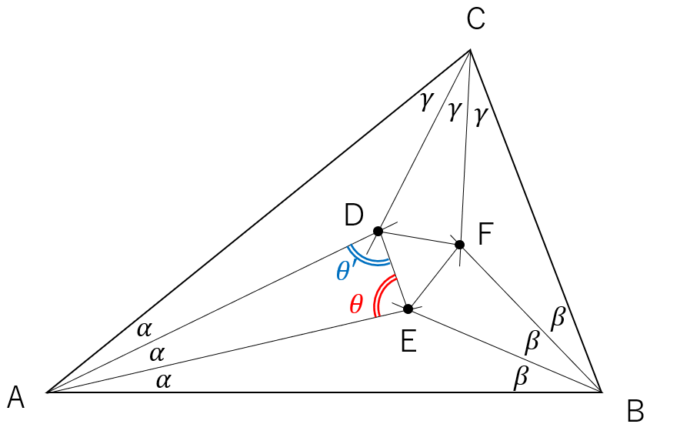
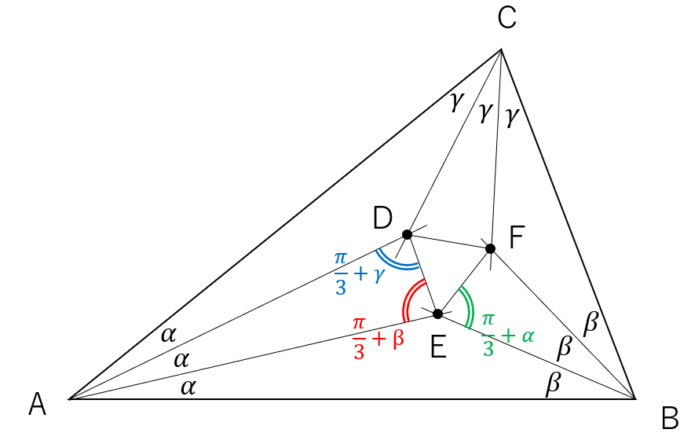
この方法から、$\angle$BEFも$\frac{\pi}{3}+\alpha$であることがわかります。$\angle$AEBは$\pi-\alpha-\beta$なので、

$$\begin{align*} \angle \text{DEF}&=2\pi-\angle \text{AED}-\angle \text{BEF}-\angle \text{AEB}\\ &=2\pi-\left(\frac{\pi}{3}+\beta\right)-\left(\frac{\pi}{3}+\alpha\right)-(\pi-\alpha-\beta)\\ &=\frac{\pi}{3} \end{align*}$$

となります！でましたね$\frac{\pi}{3}$！同様の議論により、$\angle \text{EDF}=\angle\text{DFE}=\frac{\pi}{3}$がわかり、三角形DEFは正三角形であることが証明されました！！！意外にも長かったですね！！

４．さいごに

さて今回はモーリーの定理を三角比を使って割とゴリゴリの計算で証明してきました。証明の中でも何度か現れましたが「同様に」とか「$\beta$と$\gamma$を入れ替えれてもいい」といった議論がありました。これは三角形の持つ「対称性」というものを利用しています。こうした対称性の応用の一つが幾何学模様などのデザインになっています。和からでは数学的デザインに関する無料のセミナーも開催していますので、興味のある方は是非ご参加ください！

数学的デザイン超入門

また、今回の証明のほかにも、初等幾何学的な手法や代数的な手法も知られています。特に代数的な手法に関しては余力があれば、記事にしてみようと思っています。お楽しみに！

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>