【受験直前！】入試問題から学ぶ大学数学

ロマンティック

公開日

2021年2月8日

更新日

2021年2月8日

こんにちは。和からの数学講師の岡本です。大学入試シーズンとなってきました。
ということで今回は入試問題から学ぶ面白い数学の視点をご紹介していきます。基本的に入試問題というのは、何らかの数学的な背景から問題をデザインしていくのが定番です。今回はやや古いですが、1991年の東京大学理系第4問をベースにお話ししていきます。

この記事の主な内容

１．1991年東大前期理系第4問

まずは問題をご覧ください。

（１）自然数

$n=1, 2, 3, \ldots$ に対して、ある多項式

$p_n(x), q_n(x)$ が存在して

$\begin{align*} \sin n\theta=p_n(\tan \theta)\cos^n\theta, \hspace{1.0em} \cos n\theta =q_n(\tan \theta)\cos^n \theta \end{align*}$

と書けることを示せ。
（２）このとき、 $n>1$ ならば次の等式が成立することを証明せよ。
$\begin{align*} p_n’(x)=nq_{n-1}(x), \hspace{1.0em}q_n’(x)=-np_{n-1}(x). \end{align*}$

さすがに入試問題というだけあって、なかなか難しそうですね。これを解いていくわけですが、いくつかの視点に分けてお話をしていきます。

２．困ったときは数学的帰納法

まずは、正攻法で考えます、与えられた良くわからない等式が全ての自然数で成り立つことを証明する手っ取り早く有効な方法は「数学的帰納法」です。

①

$n=1$ のときに成り立つことを確認。
②

$n=k$ で成り立っていると仮定し、

$n=k+1$ で成り立つことを示す。

数学的帰納法を絵で表すと、下のようになります。

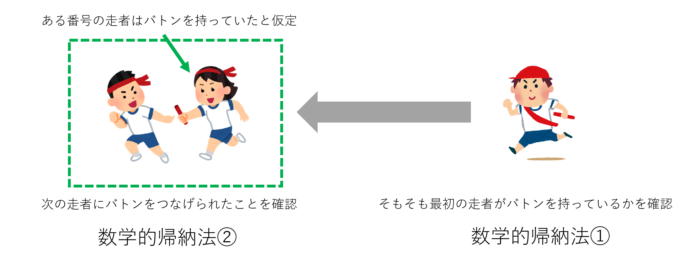
②というのは「次の走者にちゃんとバトンを渡せる」というイメージです。しかし、第1走者がバトンを持ってないと破綻してしまうので、①で確認します。こうすることで、全ての走者がきちんとバトンを持っていることが証明できます。
このような数学的帰納法を使えば、どうにか解答できるのがこの問題です。

３． $n$ 倍角の公式とチェビシェフ多項式

別の視点で見てみましょう。与えられた式をよく見てみると、この問題の本質は $\sin$ と $\cos$ の $n$ 倍角を $\cos$ と $\tan$ だけで表す公式を考えているのです。この話題には背景があり、チェビシェフ多項式が関係します。(第1種)チェビシェフ多項式とは、 $\cos n \theta$ を $\cos \theta$ の多項式で表す公式から得られます。つまり、

$\begin{align*} \cos n\theta=T_n(\cos \theta) \end{align*}$

で表される多項式 $T_n(x)$ を第1種チェビシェフ多項式といいます（第2種は $\sin$ 版なので、今回は省略します）。例えば、

$\begin{align*} \cos 2\theta=2\cos^2\theta-1,\hspace{1.0em}\cos3\theta =4\cos^3\theta-3\cos \theta \end{align*}$

であることからチェビシェフ多項式 $T_2(x), T_3(x)$ は

$\begin{align*} T_2(x)=2x^2-1, \hspace{1.0em}T_3(x)=4x^3-3x \end{align*}$

となります。チェビシェフ多項式は直交多項式といわれる、由緒正しい多項式の1種です。積分に関して重要な等式（直交関係式）などが知られています。こうした、数学的背景のある問題であることがわかります。しかし、チェビシェフ多項式が背景にあるからといって、見通しが良くなったわけではありません。別の視点で眺めてみましょう。

４．複素数の世界でワンパン

タイトルの通り、複素数の世界を考えます。いささか唐突にも見えますが、複素数の超重要定理「ド・モアブルの公式」を思い出しましょう。

(ド・モアブルの公式)

$\begin{align*} \cos n \theta+i\sin n \theta=(\cos \theta+i\sin \theta)^n \end{align*}$

この公式を眺めていると見えてきます。まず、右辺を $\cos^n\theta$ でくくります。

$\begin{align*} \cos n \theta +i\sin n \theta=(1+i\tan \theta)^n \cos^n\theta \end{align*}$

一度問題の式を思い出し、この式に当てはめてみます。

$\begin{align*} \cos n \theta +i\sin n \theta=(q_n(\tan \theta)+ip_n(\tan \theta))\cos^n \theta \end{align*}$

つまり $\tan \theta$ を $x$ でおいて考えると、
$\begin{align*} (1+ix)^n=q_n(x)+ip_n(x) \end{align*}$
であることがわかります。したがって、 $q_n(x), p_n(x)$ は $(1+ix)^n$ の実部と虚部であり、どう考えても多項式になります（もっといえば、二項展開を使えば $p_n(x)$ も $q_n(x)$ も具体的に求められちゃいます）。
さらに（２）の問題に関しても簡単です。上の式を両辺 $x$ で微分すると