１．私たちの生活とリスク

私たちの生活の中にはいろいろなリスクが存在します。たとえば、けがや病気、火災や事故、死亡など軽度なものから重たいリスクまで様々です。そういった「リスク」の中には多くの費用が必要になることがあります。貯金があればいいのですが、リスクはいつ起こるかわかりません。リスクに備えるために「保険」というものがあります。今日は保険とその背後にある数学や統計学について簡単にまとめてみようと思います。

２．保険のしくみ

加入している人たちが協力して定期的にお金を出し合い、“共有金庫”に貯めていきます。同じ加入者（仲間）の中で事故やケガなど、万が一のことが起こってしまった場合、この共有金庫からお金を補います。

このように保険とは「相互扶助の精神」で成り立っています。

３．保険金や保険料ってどんな風に決められているの？

皆さんが支払っている保険料、あるいは受け取る保険金というのはどのようにして決められているのでしょうか？実はこうした保険内容の設定には「数学」が深く関わっています。保険会社では、こうした保険の設計（保険金や保険料の算出）を行う数理のプロフェッショナル“アクチュアリー”と呼ばれる方々が活躍しています。このアクチュアリーという職業は近年非常に注目され、ますますアクチュアリーを目指す方が増えてくることでしょう。

3.1. 保険の大原理「収支相等の原理」

保険を設計する際、「収支相等の原理」という基本原理に基づいて計算します。考え非常にシンプルで、

　
という等式を保険会社の視点で考えるというものです。
一つ注意するべき点は、お金が入って来る時点と、出ていく時点は通常異なるため、どこか時点を１つ固定して受け渡しが発生するお金の「価値」を「その時点での価値」に換算して等式を立てることです。固定する時点としては「現在」が一般的です。

3.2. お金の価値、金利計算について

お金は、時間によってその価値を変えます。現金は銀行に預けることで少なからず利子を得ることができることから、例えば現在の現金100万円は1年後の現金100万円よりも価値が大きいです。

もっとも基本的なモデルとして「1年おきにお金の価値が一定の比率で上がる」というものを考えます。例えば比率を0.009とします。いま1,000円手元にあるとしましょう。この1,000円は1年後にはどれぐらいの価値になるかというとなんと1,000×1.009=1,009(素数)円になります！(1年後に素数になるなんて、素敵ですね！)

素数の謎に関してはこちら

ミレニアム懸賞金問題―リーマン予想 前編―

さて、手元の1,000円は1年後には1,009円、2年後には1,009×1.009＝1,018.018≒1,018円、3年後には1,027.2437≒1,027円、4年後には1,036.4889≒1,036円…　となっていきます。

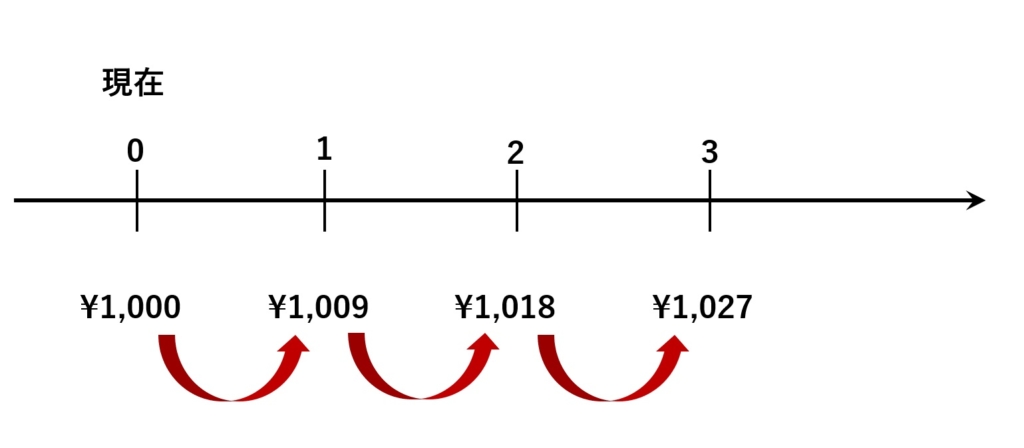
逆に1年後の1,000円は現在だとどのぐらいの価値でしょうか？

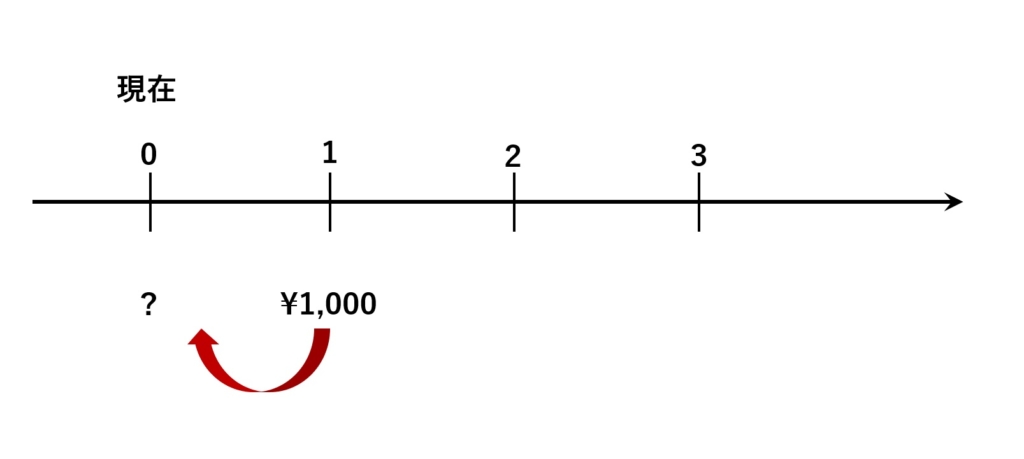
1年後にようやく1,000円になるということは、いまでは1,000円より安そうですね。実際には次のような計算で求めることができます。

　
ちなみに991も素数です。素数についてより知りたい場合はこちら

ミレニアム懸賞金問題―リーマン予想 後編―

このように、実際にこの先支払われる金額と現在の価値には差があります。こうした「金利」というものも加味して保険の等式を考えなくてはいけません。なお先ほどの例では現在の価値に変換するために「1.009で割る」という操作をしました。これは「1/1.009を掛ける」ことと同じです。この1/1.009にあたる部分を「原価率」といいます。

3.3. 実際の保険モデルを考えてみよう

具体的な保険を想定して実際に計算してみましょう。「30歳加入で3年間（保険料期始払い）」という保険で、次のような内容のものを想定しましょう。

• ・生存している加入者は年度始に保険料（定額）を支払う
• ・加入者が死亡した場合、ご家族に10万円の死亡保険金が渡される
• ・3年後の生存者には1万円の生存保険金が渡される

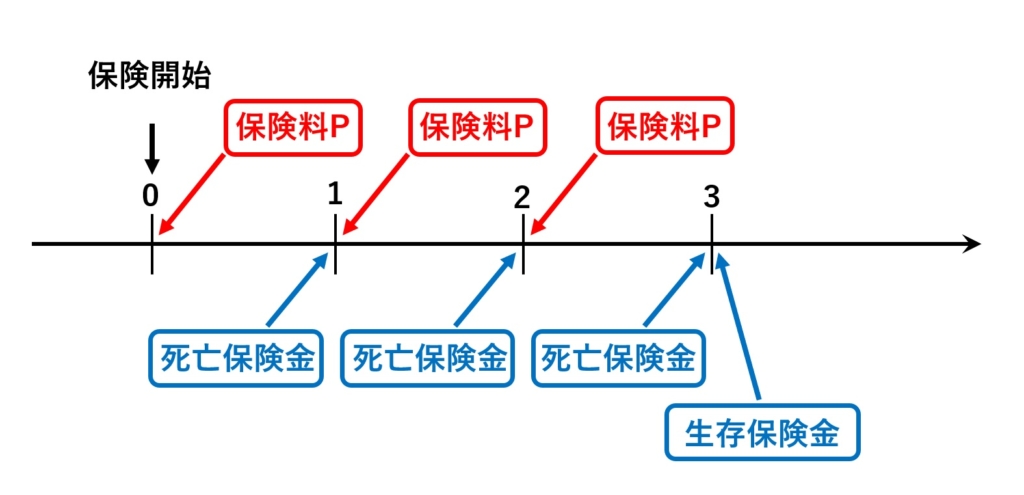
こうした保険（養老保険といいます）の保険料はいくらに設定すればいいでしょうか？

例えば30歳の加入者が保険開始時100人だったとしましょう。翌年度始の生存者は98人、2年後は95人、3年後には91人が生存していたとします。
このとき、

• ①最初の年には100-98＝2人が死亡　→　第1年度末に10万×2=200万円
• ②次の年には98-95=3人が死亡　→　第2年度末に10万×3＝300万円
• ③その次には95-91=4人が死亡　→　第3年度末に10万×4＝400万円
• ④最終的な生存者は91人　→　第３年度始に1万×91=91万円

　
これを現在の価値に戻すために原価率を掛けてあげる必要があります。ここでは先ほどと同じ金利で原価率を1/1.009としましょう。すると

• ・①は20万×1/1.009＝￥198,216.056
• ・②は30万×1/1.009×1/1.009=￥294,672.035
• ・③は40万×1/1.009×1/1.009×1/1.009=￥389,391.523
• ・④は91万×1/1.009×1/1.009×1/1.009=￥885,865.71

合計：￥1,768,145.325

これらの合計は保険会社から【出ていくお金】です。
では、【入ってくるお金】つまり加入者が支払う保険料はどうでしょうか？ここでは仮に保険料を一律P円とおきましょう。

• 保険開始時は100人生存　→　第１年度始に100×P円
• 次の年には98人生存　→　第２年度始に98×P円
• その次には95人生存　→　第３年度始に95×P円

　
これらを現在の価値に直しましょう

• ・①は100×Pが現在価値
• ・②は98×P×1/1.009=97.12586×P
• ・③は95×P×1/1.009×1/1.009=93.31281×P

合計：￥290.438678×P

こうして、保険会社の視点で【入ってくるお金】と【出ていくお金】の現在価値が計算できました。これらが一致するように（収支相等の原理より）保険料Pを求めてみましょう。
方程式は

　
となりこれをPについて解くことによりP=6,087.8438≒6,088つまり、加入者一人の保険料は年額6,088円で設定できることがわかりました。
しかし、実際のところ、その年に何人死亡するかなどは誰もわかりません。人の死は偶然に支配されていそうなのですが、大量のデータをもとに各年齢における死亡率をある程度推測することができます。いわゆる統計学の「大数の法則」と言われるものの考え方です。
さらに学習を進めていくとこの「収支相等の法則」は期待値の計算であることがわかります。より詳しい統計学や生命保険数理の授業を受けてみたいという方は数学教室をご利用ください。

数学教室和：

個別教室 – 初めての方へ

なお、死亡率というものは厚労省のホームページで「生命表」として公開されており、５年おきに改定されるようです。実際はこうした死亡率や生存率のデータに基づいて保険の式を立てています。

４．おわりに

私たちが普段いろいろなところで耳にする保険やリスクといった言葉、実はしっかりとした数学や統計学の理論があってこそ成り立っているものでした。このように考えてみると、私たちの日常生活と数学は切っても切り離せないんだなぁとより一層実感していただけると思います。

<文/岡本健太郎>
⇒ 講師紹介ページへ