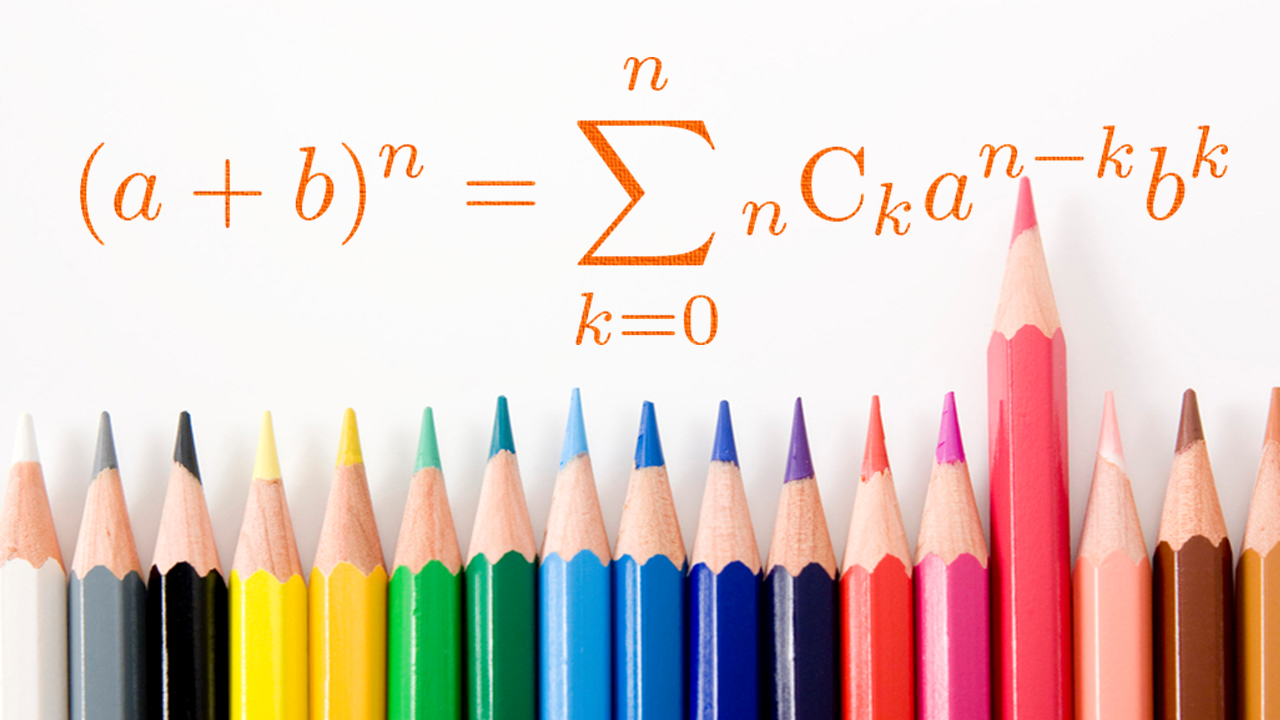
数学教室和(なごみ)講師の松中です。先日高校数学の個別授業で「二項定理」をお客様と一緒にテキストに載っていない証明を2つほど見つけました。どちらもネットで探すと簡単に見つかるレベルの証明ではありますが、見つけた瞬間はお客様と自分で見つけたオリジナル証明ではありましたので、記念に紹介したいと思います。

二項定理とは

まず、二項定理とは\((a+b)^n\)を展開した時の各項の係数が簡単に分かる高校数学の公式です。つまり、

• \(n=1\)のとき

\[(a+b)^1={\color{red}1}a+{\color{red}1}b\]

• \(n=2\)のとき

\[(a+b)^2={\color{red}1}a^2+{\color{red}2}ab+{\color{red}1}b^2\]

• \(n=3\)のとき

\[(a+b)^3={\color{red}1}a^3+{\color{red}3}a^2b+{\color{red}3}ab^2+{\color{red}1}b^3\]

• \(n=4\)のとき

\[(a+b)^4={\color{red}1}a^4+{\color{red}4}a^3b+{\color{red}6}a^2b^2+{\color{red}4}ab^3+{\color{red}1}b^4\]

と展開した時の、赤字の係数部分が簡単に分かる公式です。

よく知られている話題ですが、この赤字の数字を並べて書くと「パスカルの三角形」が出来上がります。これは第\(1\)段目の「\(1\) \(1\)」から始めて隣り合う数の和をその下に書き、各段の両端には\(1\)を書いたものです。

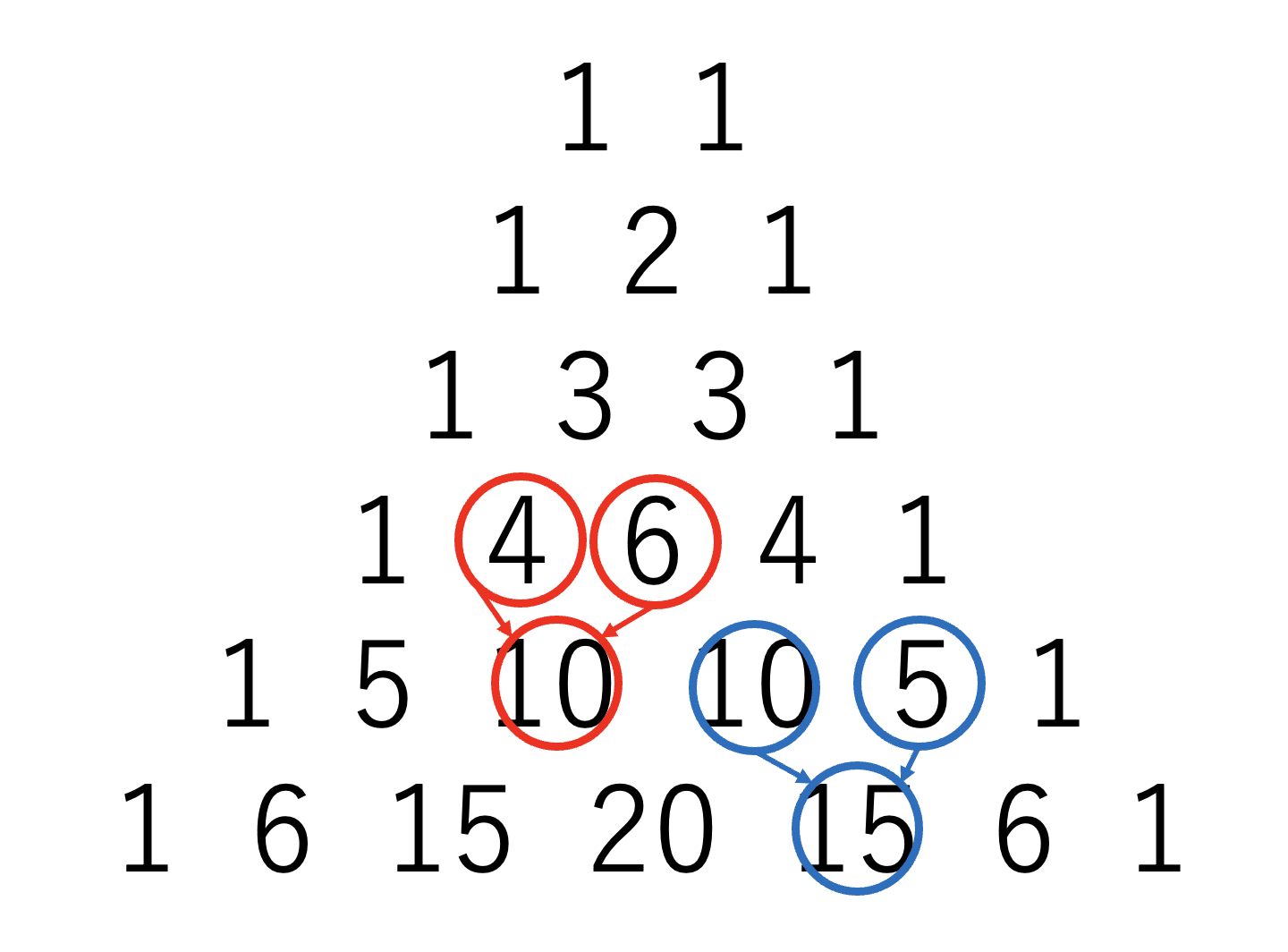
なかなか面白い三角形でパスカルの三角形さえあれば\((a+b)^n\)の係数は簡単に知ることができますが、例えば\(n=10\)の展開式の係数を知りたいときは\(10\)段も三角形を書かなければいけません。そして、そこに至るまでに多数回の足し算を行いますが、どれ\(1\)つをとっても間違えてはなりません。そう考えると\(n\)がある程度大きいときにパスカルの三角形で\((a+b)^n\)の係数を導出するのは好ましいやり方とは言えません。

そこで登場するのが「二項定理」です。

　
ここで\({}_n \mathrm{C}_k\)は異なる\(n\)個のものから\(k\)個を取り出す組合せの総数を表し、

\[
{}_n \mathrm{C}_k=\frac{n!}{(n-k)!k!}
\]
となることが知られています。例えば異なる5個のものから3個を取り出す組合せは、

　

のように\(10\)通りありますが、これは\({}_5 \mathrm{C}_3=\frac{5!}{3!2!}=10\)からも分かります。

二項定理を使うことで、例えば\((2x-3y)^8\)の\(x^3y^5\)の係数は、
\[
(2x-3y)^8=\sum_{k=0}^8{}_8 \mathrm{C}_k(2x)^{8-k}(-3y)^k
\]
の右辺で\(k=5\)の項を考えることで、\({}_8 \mathrm{C}_5 2^{3}(-3)^5=-108864\)と簡単に計算することができます。

二項定理とパスカルの三角形の関係

二項定理を使って\((a+b)^n\)の係数を書き出してみます。

• \(n=1\)のとき

\[(a+b)^1={\color{red}{{}_1 \mathrm{C}_0}}a+{\color{red}{{}_1 \mathrm{C}_1}}b\]

• \(n=2\)のとき

\[(a+b)^2={\color{red}{{}_2 \mathrm{C}_0}}a^2+{\color{red}{{}_2 \mathrm{C}_1}}ab+{\color{red}{{}_2 \mathrm{C}_2}}b^2\]

• \(n=3\)のとき

\[(a+b)^3={\color{red}{{}_3 \mathrm{C}_0}}a^3+{\color{red}{{}_3 \mathrm{C}_1}}a^2b+{\color{red}{{}_3 \mathrm{C}_2}}ab^2+{\color{red}{{}_3 \mathrm{C}_3}}b^3\]

• \(n=4\)のとき

\[(a+b)^4={\color{red}{{}_4 \mathrm{C}_0}}a^4+{\color{red}{{}_4 \mathrm{C}_1}}a^3b+{\color{red}{{}_4 \mathrm{C}_2}}a^2b^2+{\color{red}{{}_4 \mathrm{C}_3}}ab^3+{\color{red}{{}_4 \mathrm{C}_4}}b^4\]

先ほどのパスカルの三角形のルール「隣り合う数の和を下に書く」というものは、例えば\({}_5 \mathrm{C}_2+{}_5 \mathrm{C}_3={}_6 \mathrm{C}_3\)を表しており、計算すればこの例で成り立っていることが確認できます。これは一般に

　
が成り立つことを意味しています。

この関係式は今回紹介する二項定理の\(1\)つ目の証明で重要なので証明しておきましょう。

\({}_n \mathrm{C}_k={}_{n-1} \mathrm{C}_{k-1}+{}_{n-1} \mathrm{C}_{k}\)の両辺の意味を考えることによる証明

\({}_n \mathrm{C}_k\)は異なる\(n\)個の中から\(k\)個を取り出す組合せの総数です。ここでは考えやすいように\(n\)人の中から\(k\)人を選出する組合せの総数として考えましょう。

まず\(n\)人の中の特定の\(1\)人を決めます。誰でも構いませんが、\(A\)さんを選ぶことにしましょう。次に\(k\)人を選出するわけですが、選ばれた\(k\)人の中に\(A\)さんが含まれる場合と、含まれない場合があるでしょう。これらは同時に起こることはありませんから、

\({}_n \mathrm{C}_k=\)「\(n\)人から\(k\)人を選出する組合せの総数」=「\(n\)人から\(A\)さんを含む\(k\)人を選出する組合せの総数」+「\(n\)人から\(A\)さんを含まない\(k\)人を選出する組合せの総数」

が成り立ちます。

「\(n\)人から\(A\)さんを含む\(k\)人を選出する組合せの総数」は\(A\)さんは選出確定で、残りのメンバーを\(n-1\)人から\(k-1\)人選出する総数に等しいですから、これは\({}_{n-1} \mathrm{C}_{k-1}\)となります。

また「\(n\)人から\(A\)さんを含まない\(k\)人を選出する組合せの総数」は\(A\)さんを含まない\(n-1\)人の中から\(k\)人を選出する総数に等しいですから\({}_{n-1} \mathrm{C}_{k}\)となります。

よって、\({}_n \mathrm{C}_k={}_{n-1} \mathrm{C}_{k-1}+{}_{n-1} \mathrm{C}_{k}\)が成り立つことが分かります。

ここでは\({}_n \mathrm{C}_k\)の意味を考えることで証明しましたが、右辺を\({}_n \mathrm{C}_k\)の定義に沿って計算することで数式のみを用いて証明もできます。

テキストに載っている二項定理の証明

普通の高校数学のテキストに載っている二項定理の証明は以下のようなものです。私もこれまでこれ以外の証明は見たことはなかったです。

\[
(a+b)^n=(a+b)×(a+b)×・・・×(a+b) ,\,\,\,((a+b)\text{が}n\text{個並んだもの})
\]

これを展開した時の\(a^{n-k}b^k\)の係数は\(n\)個の\((a+b)\)から\(n-k\)個の\(a\)、\(k\)個の\(b\)を選出する総数に等しくなります。これは単に\(n\)個の\((a+b)\)から\(k\)個の\(b\)を選出する総数と考えてもよいので、\({}_{n} \mathrm{C}_{k}\)となり、二項定理が成り立ちつことがわかります。

当然授業でもこの方法で解説したのですが、少し騙されているような感覚があるのと、いつもこの証明で飽きてしまったので、お客様と私で新しい証明を考えるということになりました。私とお客様で興味の赴く方向に数学の話を展開できるのは個別指導の魅力かと思います。

数学的帰納法による証明

最初に思い付いたのは数学的帰納法を使う証明です。数学的帰納法は自然数\(n\)に関する命題\(P(n)\)を全ての自然数\(n\)について証明する際によく用いられます。証明したい二項定理も\((a+b)^n\)と自然数\(n\)が現れるので数学的帰納法でも証明できそうです。

数学的帰納法は次の\(2\)ステップで進みます。

• ① \(n=1\)のとき成り立つことを証明する
• ② \(n=l\)のときに成り立つことを仮定すると、\(n=l+1\)の時も成り立つことを証明する

数学的帰納法の詳しい説明についてはこちらの記事をご参照ください。

数学的帰納法は本当に帰納法なの？

それでは二項定理\((a+b)^n=\sum_{k=0}^n{}_n \mathrm{C}_ka^{n-k}b^k\)を数学的帰納法を用いて証明しましょう。

① \(n=1\)のとき成り立つことを証明する

\[
\text{(左辺)}=(a+b)^1=a+b=\text{(右辺)}
\]

となり正しいです。

② \(n=l\)のときに成り立つことを仮定すると、\(n=l+1\)の時も成り立つことを証明する

\(n=l\)のとき二項定理が成り立つと仮定します。つまり、
\[
(a+b)^l=\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^k
\]
が成り立つとします。
両辺に\((a+b)\)をかけると、(左辺)は\((a+b)^{l+1}\)となり、(右辺)は、

\[
\text{(右辺)}=(a+b)\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^k=\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k+1}b^k+\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^{k+1}
\]

となります。

ここで、最右辺\(1\)項目の\(\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k+1}b^k\)から\(k=0\)を\(\sum\)から出すことにすると、
\[
\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k+1}b^k=a^{l+1}+\sum_{k=1}^l{}_l \mathrm{C}_ka^{l-k+1}b^k
\]
となります。

また、最右辺\(2\)項目の\(\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^{k+1}\)から\(k=l\)を\(\sum\)から出すと、
\[
\sum_{k=0}^{l}{}_l \mathrm{C}_ka^{l-k}b^{k+1}=\sum_{k=0}^{l-1}{}_l \mathrm{C}_ka^{l-k}b^{k+1} + b^{l+1}
\]
となります。ここで、\(\sum\)の添え字\(k\)を\(k^{\prime}=k+1\)に変更します。元々\(k\)は\(0\)から\(l-1\)まで動いていたので、\(k^{\prime}\)は\(1\)から\(l\)まで動くことになるので、
\[
\sum_{k=0}^{l-1}{}_{l} \mathrm{C}_ka^{l-k}b^{k+1}=\sum_{k^{\prime}=1}^l{}_l \mathrm{C}_{k^{\prime}-1}a^{l-k^{\prime}+1}b^{k^{\prime}}
\]
となります。この形にしてから改めて\(k^{\prime}\)を\(k\)と書き直すことで、先ほどの最右辺\(2\)項目は次の形にまとまります。
\[
\sum_{k=0}^{l}{}_l \mathrm{C}_ka^{l-k}b^{k+1}=\sum_{k=1}^{l}{}_l \mathrm{C}_{k-1}a^{l-k+1}b^{k} + b^{l+1}
\]

長くなりましたが、最終的に(右辺)は
\begin{align*}
\text{(右辺)}&=(a+b)\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^k=\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k+1}b^k+\sum_{k=0}^l{}_l \mathrm{C}_ka^{l-k}b^{k+1}\\
&=a^{l+1}+\sum_{k=1}^l{}_l \mathrm{C}_ka^{l-k+1}b^k+\sum_{k=1}^{l}{}_{l} \mathrm{C}_{k-1}a^{l-k+1}b^{k} + b^{l+1}\\
&=a^{l+1}+\sum_{k=1}^l\{{}_l \mathrm{C}_k +{}_l \mathrm{C}_{k-1} \}a^{l-k+1}b^k +b^{l+1}\\
&=a^{l+1}+\sum_{k=1}^l{}_{l+1} \mathrm{C}_ka^{l-k+1}b^k+ b^{l+1}=\sum_{k=0}^{l+1}{}_{l+1} \mathrm{C}_ka^{l-k+1}b^k
\end{align*}

となります。ここで、先に証明した\({}_l \mathrm{C}_k +{}_l \mathrm{C}_{k-1} ={}_{l+1} \mathrm{C}_{k}\)と、\({}_{l+1} \mathrm{C}_{0}={}_{l+1} \mathrm{C}_{l+1}=1\)を用いています。

以上から、
\[
(a+b)^{l+1}=\sum_{k=0}^{l+1}{}_{l+1} \mathrm{C}_ka^{l+1-k}b^k
\]
となり、\(n=l+1\)のときにも二項定理が成り立つことが分かり、数学的帰納法から証明が完結します。

テイラー展開による証明

次にテイラー展開を用いて証明しました。テイラー展開とは以下の公式で、高校数学では学ばないのですが、お客様は元々大学数学も学ばれていたので、テイラー展開もご存知でした。

　
証明のために\(f(x)=(x+a)^n\)とおきましょう。この\(f(x)\)をテイラー展開するため、微分していきます。
\begin{align*}
f^{\prime}(x)&=n(x+a)^{n-1}\\
f^{\prime\prime}(x)&=n(n-1)(x+a)^{n-2}\\
f^{\prime\prime\prime}(x)&=n(n-1)(n-2)(x+a)^{n-3}\\
& \vdots\\
f^{(k)}(x)&=n(n-1)(n-2)\cdots(n-k+1)(x+a)^{n-k}\\
& \vdots
\end{align*}
と続いていきます。これから\(k>n\)の時は\(f^{(k)}(x)=0\)が分かるので、テイラー展開も第\(n\)項までで展開が完了します。

よって\(k\leq n\)のとき、
\[
f^{(k)}(0)=n(n-1)(n-2)\cdots(n-k+1)a^{n-k}=\frac{n!}{(n-k)!}a^{n-k}
\]
となり、\(f(x)\)のテイラー展開は、
\[
f(x)=\sum_{k=0}^n\frac{f^{(k)}(0)}{k!}x^k=\sum_{k=0}^n\frac{n!}{k!(n-k)!}a^{n-k}x^k=\sum_{k=0}^n{}_{n} \mathrm{C}_{k}a^{n-k}x^k
\]
が分かります。\((a+b)^n=f(b)\)ですから、これに\(x=b\)を代入することで、
\[
(a+b)^n=f(b)=\sum_{k=0}^n{}_{n} \mathrm{C}_{k}a^{n-k}a^{n-k}b^k
\]
となり、これは二項定理そのものです。

まとめ

数学の世界ではある時点で学んだ定理が、より進んだ数学を学ぶことで別の視点から証明できるようになったり、意味付けできるようになったりすることが多々あり、面白いです。今回紹介したテイラー展開による二項定理の証明もそのような例の一つになっています。

実は他にも二項定理の証明がないか考えてはみたのですが、今回紹介したもの以外は思いつきませんでした。また今回の証明はネットで探せば出てくるものであり、残念ながらオリジナルのものではありませんでした。皆さんも良く知られている定理のオリジナルの証明を探してみてはいかがでしょうか。

<文/松中>

■本記事の内容を詳しく知りたい方は、こちらの講座がおすすめです。

順列と組み合わせ