数学的帰納法は本当に帰納法なの？

算数・物理・数学トピック

公開日

2020年7月29日

更新日

2020年7月29日

皆さんこんにちは。和からの数学・統計講師の川原です。

以前私は帰納法と演繹法についての記事を書きましたが、数学になじみのある方は帰納法と聞けば数学的帰納法を思い出すのではないでしょうか。本日は数学的帰納法についてお話してみます。

この記事の主な内容

数学的帰納法とは何か

まず数学的帰納法とは数学の証明法の一つで、自然数に関しての命題 $P$ が任意の自然数 $n$ に対して成り立つことを証明する手法です。といっても、数学になじみのない方は何のことかわからないと思いますので、具体例をもとに簡単に説明してみます。

命題

$4^n-1 (n=1,2,3,…)$ は

$3$ の倍数であることを示せ

　
これはどういう問題の主張は、 $n$ にどんな自然数 $(1,2,3,…)$ を入れても $4^n-1$ は $3$ の倍数になってしまう、らしいのです(不思議ですね)。それを確かめなさいという問題なのですが、具体的にいくつか確かめてみましょう。

・ $n=1$ のとき
$4^n-1=4^1-1=3$

となって、確かに $3$ は $3$ の倍数です。 $n=2$ でも確かめてみましょう。

・ $n=2$ のとき
$4^n-1=4^2-1=16-1=15$

となって、確かに $15$ は $3$ の倍数です。もうひとつ $n=3$ でも確かめてみましょう。

・ $n=3$ のとき
$4^n-1=4^3-1=64-1=63$

となって、 $63$ も確かに $3$ の倍数です。

$n$ の値を $1～3$ まで確認してみたところ確かに $4^n-1$ は $3$ の倍数になっていることが確かめられました。しかし今はたった3つの具体例を確かめただけなので、これだけではすべての $n$ について命題が成り立つかどうかはわかりません( $n=4$ では成り立たないかもしれませんね)。すべての $n$ について命題が成り立つことを証明するにはどうすればよいでしょうか。そこで出てくるのが数学的帰納法という証明法です。数学的帰納法とは次の2つを示すことによって命題が成り立つことを証明する方法です。

(1)

$n=1$ のとき命題が成り立つことを示す
(2)

$n=k$ のとき命題が成り立つと仮定すると、

$n=k+1$ のときも命題が成り立つことを示す

　
この2つは何をやっているのでしょうか。

数学的帰納法をドミノ倒しで例えてみる

この数学的帰納法をドミノ倒しで例えてみます。例えば $n=1$ で命題が成り立つことを1番目のドミノが倒れる、 $n=2$ で命題が成り立つことを2番目のドミノが倒れる、というように例えてみると、すべての自然数で命題が成り立つかどうかを確かめるということはすべてのドミノが本当に倒れるかということを確かめればよいということになります。

それではすべてのドミノが倒れることをどのように確かめればよいかというと

① 1番目のドミノが本当に倒れるかどうか
② すべてのドミノがきちんと並んでおり、前のドミノが仮に倒れたら次のドミノも倒れる

　
ということを確かめれば、連鎖してすべてのドミノが倒れるということができます。

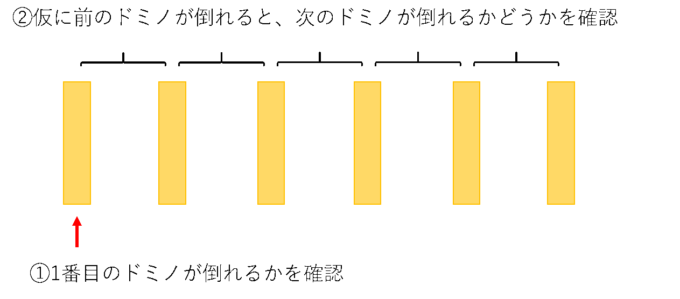
なぜなら、①より1番目のドミノが倒れると言えて、②より前のドミノが倒れると次のドミノも倒れるので、2番目のドミノも倒れます。2番目のドミノが倒れるので、②より前のドミノが倒れると次のドミノも倒れるので、3番目のドミノも倒れます。

このように連鎖して順々にドミノが倒れると言えるので、すべてのドミノが倒れるということができます。実はここで確かめた①と②が上の数学的帰納法における(1)と(2)に当たります。

(1)

$n=1$ のとき命題が成り立つことを示す
(2)

$n=k$ のとき命題が成り立つと仮定すると、

$n=k+1$ のときも命題が成り立つことを示す

　
(2)はあるドミノ( $k$ 番目)のドミノが仮に倒れるとしたら、次のドミノ( $k+1$ 番目のドミノ)も倒れるかを見ているわけですね。これが数学的帰納法の構造です。この方法を使って上の命題を証明してみましょう。

命題(再掲)

$4^n-1 (n=1,2,3,…)$ は

$3$ の倍数であることを示せ

　
(1) $n=1$ のとき
$4^n-1=4^1-1=3$
となって確かに $4^n-1$ は $3$ の倍数になるので $n=1$ のとき命題は成り立ちます。
(これで1番目のドミノが確かに倒れる、ということをいうことができました)

(2) $n=k$ のとき命題が成り立つと仮定、つまり $4^k-1$ が $3$ の倍数になると仮定すると、 $n=k+1$ のとき命題が成り立つかどうかを確かめてみます。

$4^k-1$ が $3$ の倍数になると仮定するので、整数 $m$ を使って $4^k-1=3m$ と表しておきます。
すると、 $n=k+1$ のとき、 $4^{k+1}-1$ (← $4^n-1$ の $n$ に $k+1$ を代入したもの)が $3$ の倍数になるかを見てみます。

$4^{k+1}-1=4^k⋅4^1-1=4⋅4^k-1$
$=3⋅4^k+1⋅4^k-1=3⋅4^k+3m=3(4^k+m)$

$3(4^k+m)$ は「 $3$ ×整数」の形になっているので確かに $4^{k+1}-1$ は $3$ の倍数となります。

(1)(2)より数学的帰納法が成り立ちすべての自然数 $n$ について命題が成り立つと証明できました。

数学的帰納法と帰納法の関係

さてここで数学的帰納法とは本当に帰納法なのかという疑問がわいてきます。論理的思考には帰納法と演繹法という考え方がありまして、簡単に説明すると

演繹法
「一般論や普遍的な法則と具体的な事実から、具体的な事象の結論を導く」

帰納法
「具体的な数々の事実から、それらに共通する一般論や普遍的な法則を見つける」

となります。

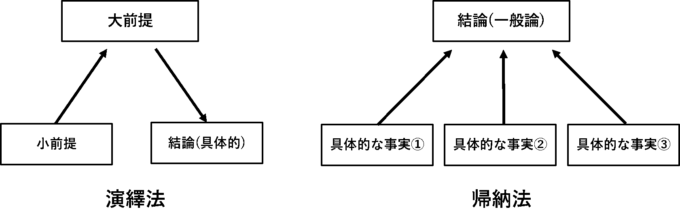
(詳しくは前回の記事をご覧ください)

この考え方で数学的帰納法を見てみます。(1)と(2)が言えたとすると(1)と(2)から $n=2$ で命題が成り立つと言うロジックは下の図より演繹法です。

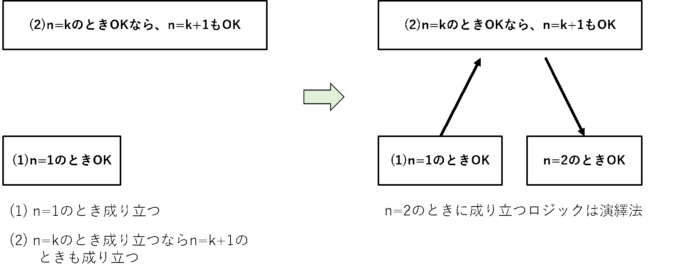
この演繹法を繰り返して具体的な例( $n=1,2,3,…$ )をたくさん作ります。

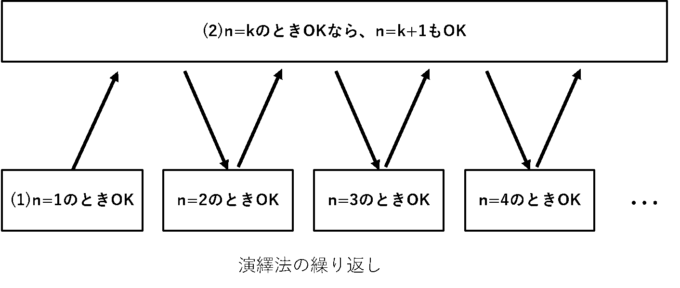
そしてたくさん作成した具体例からすべての $n$ について命題が成り立つと一般化します。

このたくさんの具体例からすべての $n$ について命題が成り立つと結論付ける箇所が帰納法に見えることからこの方法は数学的帰納法と呼ばれるようになりました。しかし実際に行っていることは演繹法によってすべての $n$ で命題が成り立つことを見ているわけなので数学的帰納法は原理的には演繹法なわけです。なんとも混乱するネーミングですね。