やばそうな数式(意味編)~キラキラ数学プロジェクト~
公開日
2020年10月4日
更新日
2020年10月4日
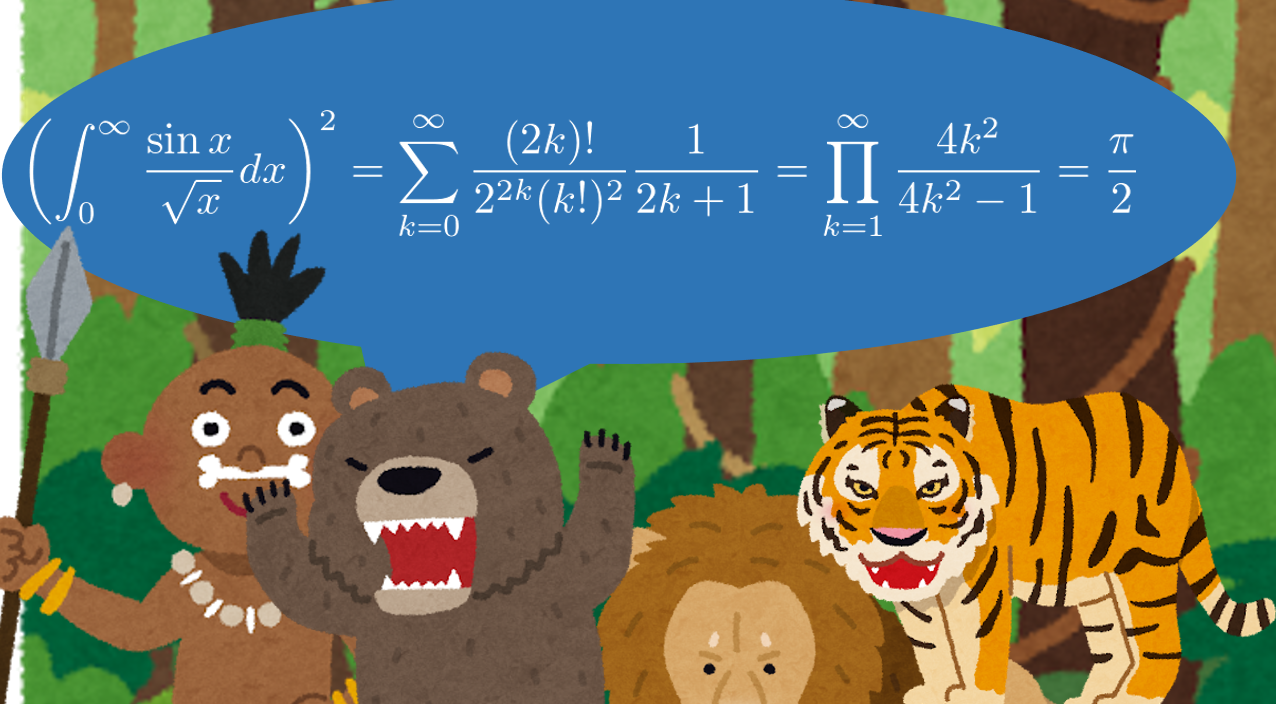
数学教室和(なごみ)講師の松中です。
先日和(なごみ)のオンライン打ち合わせの後に、キラキラ数学プロジェクトの一環として社内スタッフにやばそうな数式を紹介しました。
今回紹介するやばそうな数式は私が担当しているロマンティック数学系事業の業務の中でたまたま私がネットで見つけたものです。
本記事とほぼ同じ内容を社内スタッフに解説している動画もありますので、聴覚優位の方は動画をご視聴ください。
この記事の主な内容
ロマンティック数学系事業とは
ロマンティック数学系事業とは、「ロマンティック数学ナイト」、「ロマンティック数学ゼミ」、「ロマ数トレラン」の総称です。
ロマンティック数学ナイト
ロマンティック数学ナイトは年に数回行っている数学のお祭り、数学のプレゼン大会です。今年はコロナの影響があり、5月に初めてオンラインで開催しました。
ロマンティック数学ナイトに参加すると様々な分野、様々なレベルのロマンあふれる数学のプレゼンを聞くことができ、数学のロマンを楽しむことができます。数学が苦手な人からは敬遠されがちなイベントなのですが、心配はいりません!運営でありかつ数学好きの私でもわからないことの方が多いです。「わからないを楽しもう!」がコンセプトです!

ロマンティック数学ゼミ
「ロマンティック数学ナイトで感じた数学のロマンをもっと詳しく知りたい」という声から生まれたのがロマンティック数学ゼミです。ロマンティック数学ゼミはいわば数学の世界の観光旅行です。数学の世界には「フェルマーの最終定理」や「不完全性定理」など美しい観光名所がたくさんあります。そういった世界をロマンティストの先生が案内してくれるのです。
ロマ数トレラン
ロマ数ゼミは数学の世界の観光旅行でしたが、「旅行ではなくガッツリ数学の世界に入って自分の足で歩いて深く理解したい。」というコンセプトからロマ数トレランが生まれました。ロマ数トレランは、ロマン溢れる数学を語ることができる講師による、講義形式ではなく、双方向の対話に重きをおいた受講者参加型の少人数制ゼミです。実際に手を動かしたり、しっかりと質問、議論をする時間を設けることで内容を確実に理解することを目標とします。同じ気持ちをもった仲間と一緒に学んだ先には新しい数学の世界が待っています。ロマ数トレランではロマンティストの先生と仲間たちと一緒に演習、対話をメインとしながらその分野の深い理解を目指します。

やばそうな数式
前節は私がロマンティック数学系事業を説明するときによく用いるものです。数学の世界には獰猛な野獣が住んでいることの例として、資料の中にやばそうな数式の画像を入れています。
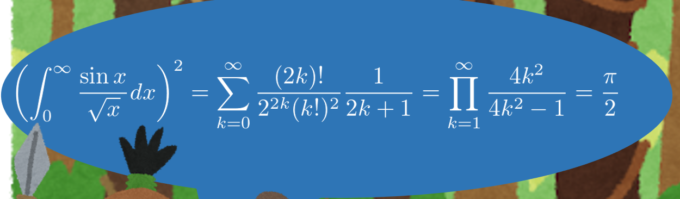
先日ロマ数トレランのガイダンス回にて、「この数式は何者か?」と聞かれました。意味は分かるものの、なぜ成り立つかなどを即答することができませんでした。
証明もしていないものを軽々と載せてしまったことを反省し、本記事と次の記事の2記事に渡ってこの数式の意味の解説、そして証明を行いたいと思います。本記事ではまず意味を解説します。
この数式は、
\[
\begin{align*}
\left( \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx \right)^2 &=\frac{\pi}{2}\\\\
\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} &=\frac{\pi}{2}\\\\
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1} &= \frac{\pi}{2}
\end{align*}
\]
という3つの等式が合わさったものです。上から積分、総和、総乗と名付けそれぞれの意味を見ていきましょう。
積分
積分はグラフと\(x\)軸で囲まれた面積を求めるものでした。
最初の等式はつまり、
\[
\int_0^\infty \frac{\sin{x}}{\sqrt{x}}dx=\sqrt{\frac{\pi}{2}}\,\,\,\text{or}\,-\sqrt{\frac{\pi}{2}}
\]
を意味します。
\(\displaystyle {y=\frac{\sin{x}}{\sqrt{x}}}\)のグラフを描くと以下の図のようになります。
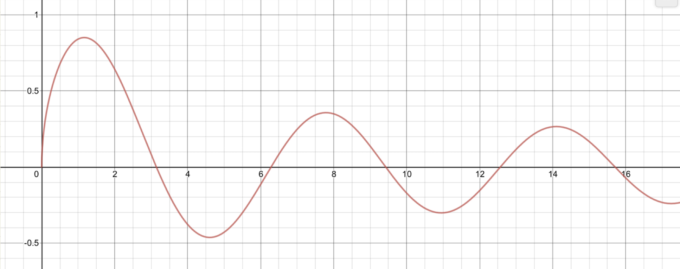
この積分はつまり、図の色を塗った部分の和になります。ただし注意したいのは、\(x\)軸より下側の部分(ピンクで塗った部分)の面積はマイナスとして和を取ることです。
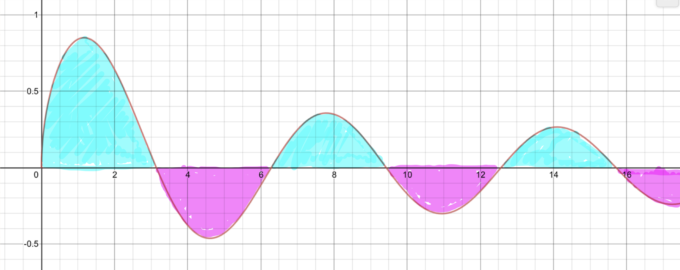
この面積の和が\(\displaystyle \sqrt{\frac{\pi}{2}}\)または\(-\displaystyle \sqrt{\frac{\pi}{2}}\)になるのです。
次記事の証明で明らかにするのですが、この面積の和は\(\displaystyle \sqrt{\frac{\pi}{2}}\)になります。こんなぐにゃぐにゃしてよくわからない面積を計算して、\(\displaystyle \sqrt{\frac{\pi}{2}}\)になるとはとても不思議ですね。
総和
これは高校でも習ったシグマを使った式です。シグマの右に書かれている式に\(k=0\)、\(k=1\)、\(k=2\)と入れて足していくと、\(\displaystyle \frac{\pi}{2}\)に近づくという意味です。
\begin{align*}
\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1} &=\frac{(2\cdot 0)!}{2^{2\cdot 0}(0!)^2} \frac{1}{2\cdot 0+1} +\frac{(2\cdot 1)!}{2^{2\cdot 1}(1!)^2}\frac{1}{2\cdot 1+1} +\frac{(2\cdot 2)!}{2^{2\cdot 2}(2!)^2} \frac{1}{2\cdot 2+1}+ \cdots\\\\ &=\frac{\pi}{2}
\end{align*}\]
実際に計算してみます。無限まで計算するのは無理なので、pythonで\(k=10000\)まで計算してみました。
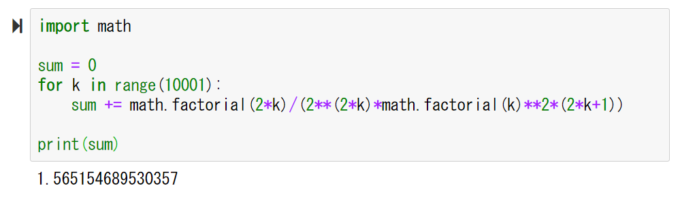
出てきた答えを2倍すると、

たしかに円周率\(3.14\cdots\)に近くなりました。厳密に一緒になっていないのは\(k=10000\)で止めているためです。
図形を用いずに円周率の値を計算したくなったら、この式を延々と計算していけばよいわけです。ただ収束はとても遅いです。
総乗
最後は総乗です。\(\displaystyle \prod\)という記号は見たことない方の方が多いのではないでしょうか。これは実はギリシャ文字\(\pi\)の大文字で、「パイ」と読みます。これは\(\displaystyle \sum\)の親戚で、\(\displaystyle \sum\)は和を取る操作であったことに対して、\(\displaystyle \prod\)は積を取る操作になっています。
つまり、
\[
\prod_{k=1}^{\infty}a_k=a_1\times a_2 \times a_3 \times a_4 \times \cdots
\]
ということです。今回の数式に当てはめると、
\[
\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1}=\frac{4\cdot 1^2}{4\cdot 1^2 – 1}\cdot\frac{4\cdot 2^2}{4\cdot 2^2 – 1}\cdot\frac{4\cdot 3^2}{4\cdot 3^2 – 1}\cdots = \frac{\pi}{2}
\]
となります。こちらも不思議ですね。
今回も実際に計算してみましょう。総和の時と同様に無限まで計算するのは無理なので、pythonを使って\(k=10000\)まで計算してみました。
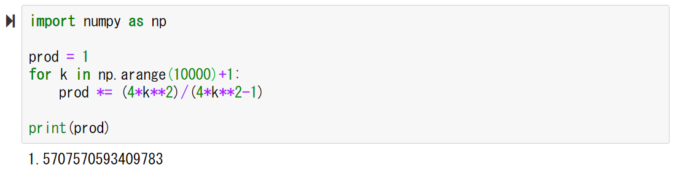
結果を2倍すると、

たしかに円周率に近くなりました。
まとめ
今回はやばそうな数式の意味について解説しました。円周率と言えば円周と直径の比ですが、今回の3つの数式から、
\[
\begin{align*}
\pi &= 2\left( \int_{0}^{\infty} \frac{\sin x}{\sqrt{x}} dx \right)^2\\\\
\pi &= 2\sum_{k=0}^{\infty} \frac{(2k)!}{2^{2k}(k!)^2} \frac{1}{2k+1}\\\\
\pi &= 2\prod_{k=1}^{\infty} \frac{4k^2}{4k^2 – 1}
\end{align*}
\]
のように円周率を定義してもよいのです。円周率をこれらのいずれかの等式で定義した場合、「円周と直径の比」というそもそもの円周率の定義は、性質、定理に姿を変え、証明すべき対象になります。今回紹介した数式は円周率を表す数式の一例にすぎず、他にも様々な表示があります。そう考えると円周率というのは何かとんでもなく普遍的な定数で、「円周と直径の比」という性質は円周率の側面オブ側面なのかもしれませんね。
次回の記事からこれらの等式を証明していきます。なんと積分の証明には以前紹介した複素関数が現れます。実数の世界で定義された関数を実数の世界で積分したいだけなのに複素関数の力を必要とするところに、複素関数の威力が感じられます。お楽しみに。
<文/松中>














