こんにちは。和からの数学講師の岡本です。今回は前回お話した「石取りゲーム」の続きをお話していきたいと思います。ぜひこちらも併せてご覧ください。

先手必勝！？戦略とゲーム理論（初級編）

１．復習：石取りゲームのルール確認

　まず、石取りゲームのルールを確認しておきましょう。まず２人対戦のゲームであり、先攻と後攻を決めます。複数の石をいくつかの山に分けておき、先攻から石を取っていき、石が取れなくなった方が負けです。もちろん石の取り方にはルールがあります。

①いくつ取ってもいいが、必ず１つ以上取ること。
②同じ山からしか取れない（複数の山から同時に石を取ることはできない）。

このルールのもと、今回は山３つで進めていきたいと思います。

２．３つの山で対戦

　今回もAさんとBさんに登場してもらいましょう。山Xは7個、山Yは5個、山Zは3個とし、Aさんが先攻です。

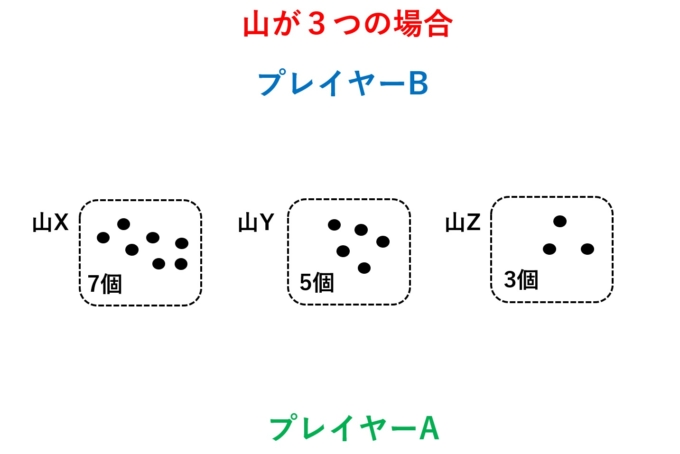
Aさん「う～ん、最初はどうするか迷うなぁ。では一番多い山のXから５個取っちゃいます。」

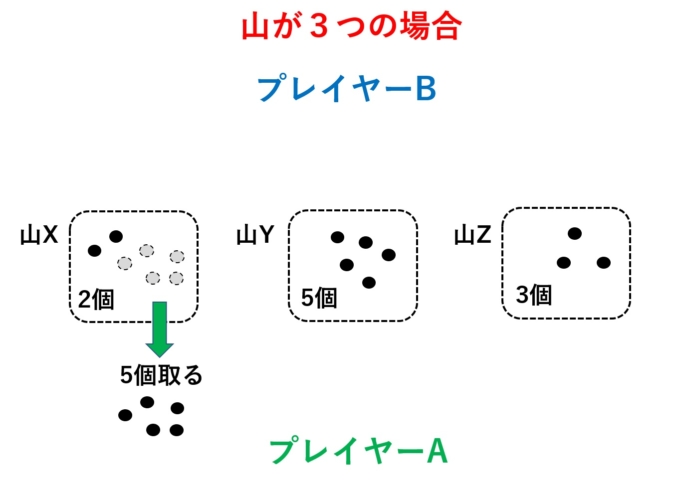
Bさん「かなり減りましたね！じゃあ、何となくYから4つ取ることにします。」

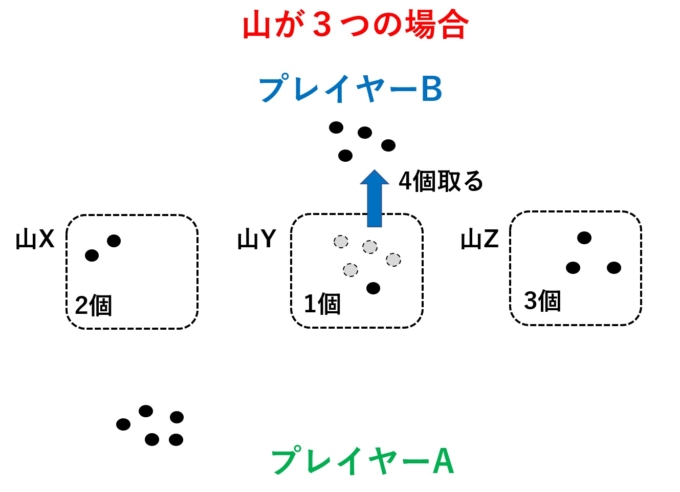
鋭いAさん「（…！？これってもしかして、僕負け決定…？）とりあえず、Zから３個全部取ります。。。」

<

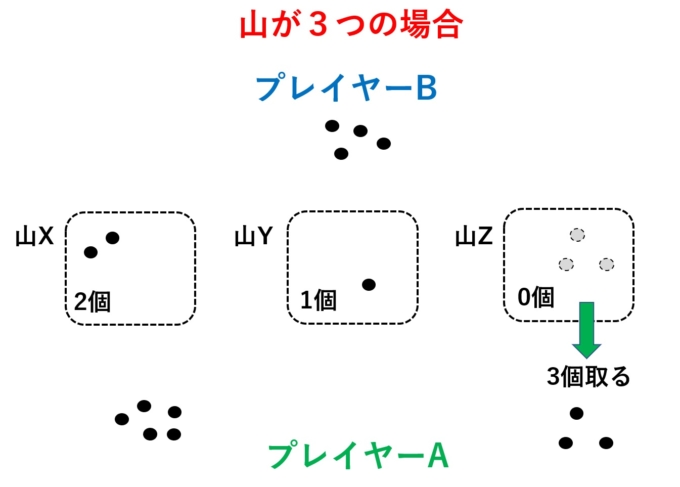
にやけるBさん「これは２つの山の場合と同じだね！ということはXから１個取って山の数を同じにすればいいんだね！★」

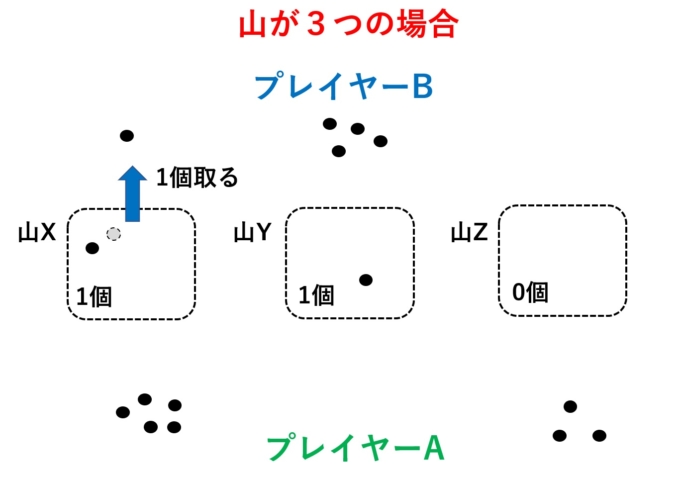
敗北を確信するAさん「（無言でXから１個取る）」

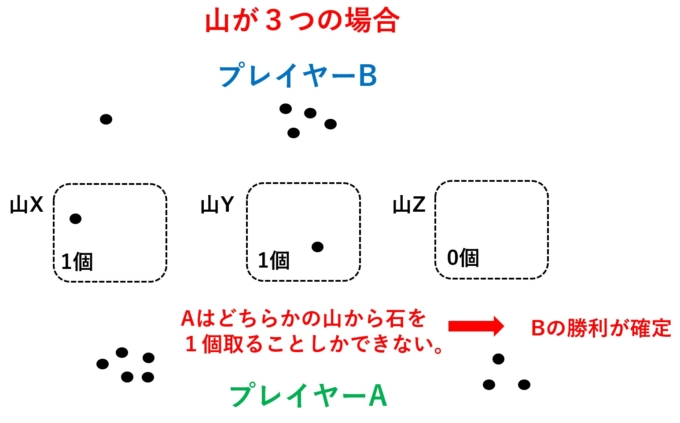
こうして、最後の１つをBさんが取ることで、Bさんの勝利が決定しました。いかがでしょうか？負けを読んでいたAさんも鋭かったわけですが、こんなゲームに必勝法なんてあるのでしょうか。

３．Aさんがとるべきだった一手

　必勝法は実はあります。方法を知っていれば、なんとAさんは確実に勝利していたのです。Aさんが取るべき最初の一手は、どこの山でもいいので、「1つ石を取る」だけです。たとえばXから１個石を取ったとしましょう。

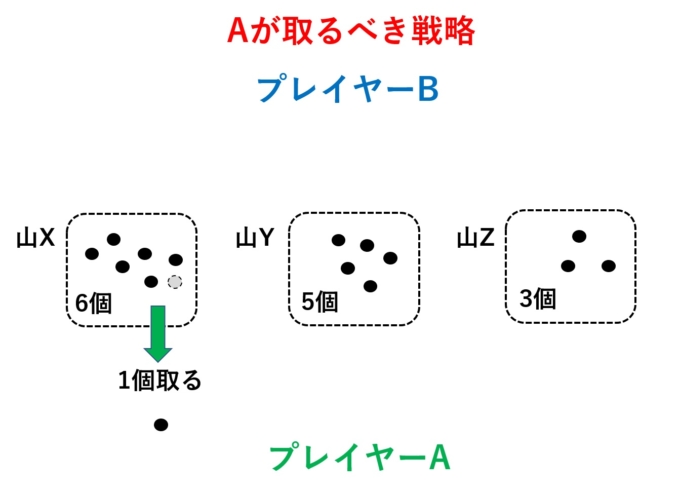
驚くべきことに、この後Bさんがどんな手を打とうと、確実にAさんが勝てる状況に持ち込めたのです。前回の話（２つの山の場合）の教訓から、Bさんが少なくともやってはいけない手は「同数の山を作る」ことです。例えばYから２個石を取ると(X,Y,Z)=(6,3,3)となります。するとAさんは同数でないXの山を全て取り去ることで、「同数２山」の状態に持ち込めます。それを踏まえて、例えばBさんがYから４個石を取ったとしましょう。

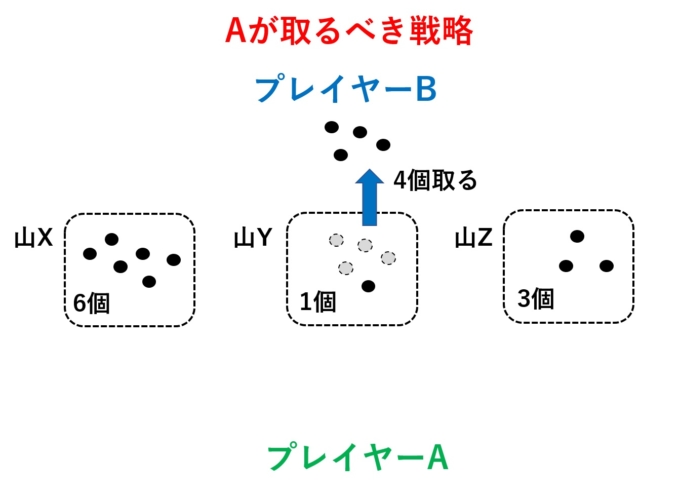
するとAさんは取るべき一手は先ほどの対戦の教訓からXの山から4個取ることで(X,Y,Z)=(2,1,3)にします。先ほどの対戦で明らかなように、山の数が(1,2,3)になった時点でと相手の打つ手はなくなります。つまり、Aさんの勝利になります。

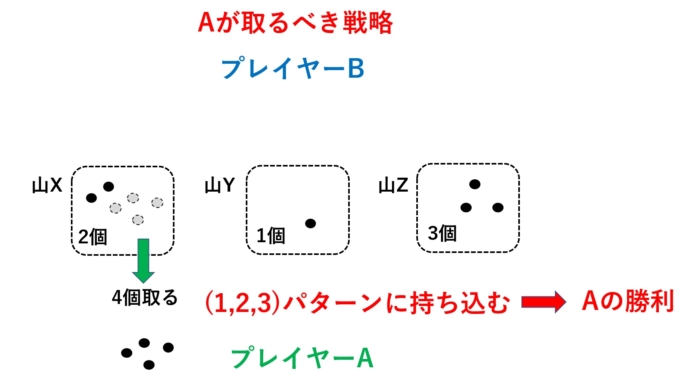
とにかく恐ろしいのは、Bさんがどんな手を打っても、Aさんには必ず“神の一手”が存在することです。そして何より、数学（ゲーム理論）を使うことで戦況を支配することができるのです。これがゲーム理論の面白さです。

５．さいごに

いかがでしたでしょうか。せっかくなので、(7,5,3)の状況からAさんが勝利するまでのルートを以下にまとめてみました（ただし、２山にする、同数の山を作ることは避けています）。

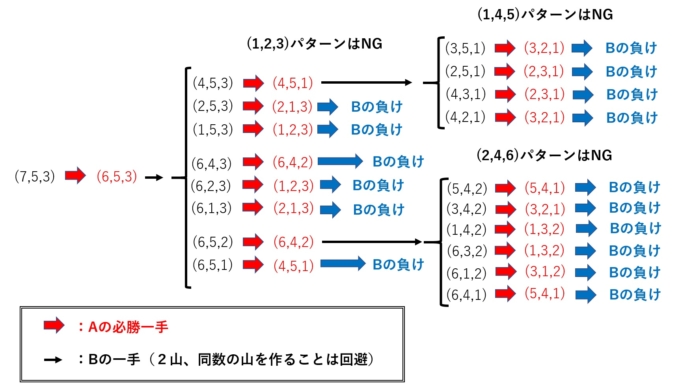
こうしてみると、最初に山の石の数が7、5、3個である場合、先攻のAさんが必勝一手を行うとBさんははじめからなす術がないことが分かります。次回はいよいよ、数学を使った解説を行います。必ず存在する「神の一手」を極めましょう！お楽しみに！

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>