【Excelアート】ランダムな曲線を作成してみた。
公開日
2023年12月31日
更新日
2023年12月31日

みなさんこんにちは!和からの数学講師の岡本です。今回は以前から個人的に考えていた「ランダムな曲線をExcelで作成することができるか?」というお話です。なお、これは「数式を使って「面白い曲線」を描きたい」シリーズの続きになります。以前までの内容をご覧になりたい方はこちらをどうぞ!
この記事の主な内容
1.Excelを使って円を描く
Excelには「散布図」というグラフがあり、2つの数値データの関係性を平面的に表すことができます。データ間の関係性はさておき、散布図とは、2組の数値データを平面上の\(x\)座標、\(y\)座標として描写できるツールだと考えることができます。そこで、高校数学で登場する\(\sin\theta\)や\(\cos\theta\)などを用いることで、円周上の点を表現することができます。
Excelの関数にCOS関数やSIN関数というものがあるので、それらを用いれば、非常に簡単に円上の点のデータを作成することができ、これらを線で結ぶことで、円(正確には正多角形)を作成することができます。
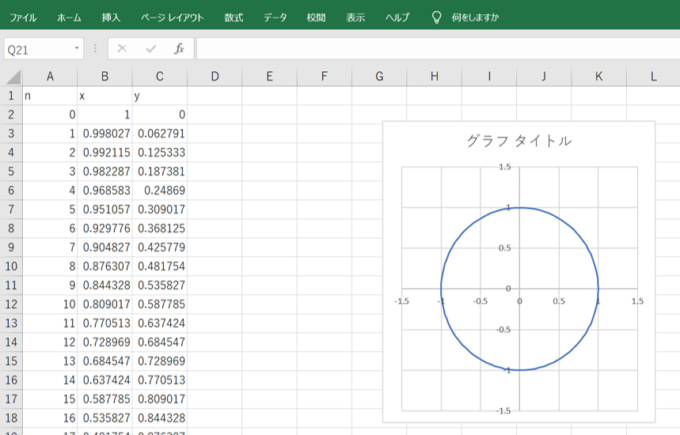
円という曲線は、スタート地点とゴール地点が同じであるような曲線(閉曲線といいます)の中で最も単純なものになります。今回の話題は、円のような「お行儀のよい」曲線ではなく、もっと自由な、ランダムな閉曲線というものをExcelで表現できないかというお話です。
2.ランダムな曲線を作るためのアイデア
ランダムな閉曲線とは、次にようなものを想定しています。
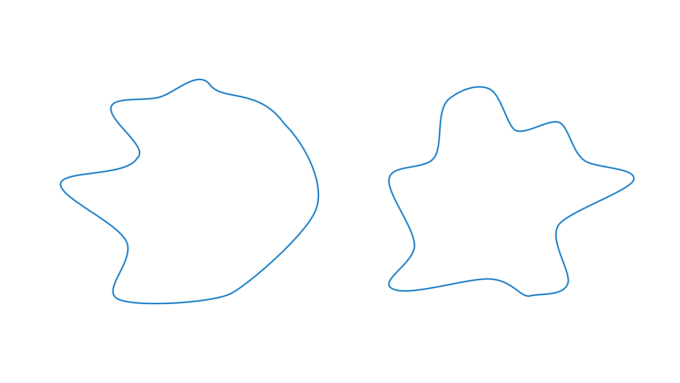
このような自由な動きをする曲線はどのようにすれば描くことができるでしょうか?ランダムな動きを入れたいので、Excelの「乱数」を使用したいなぁと思いながら、岡本はぼーっと考えていました。そんなある日、ふと次のようなアイデアにたどり着きました。
「角度によって半径の大きさをランダムに変化させればいいのでは?」
つまり、\(\cos\theta\)と\(\sin\theta\)の前に角度\(\theta\)で変化する半径の関数\(r(\theta)\)を考えます。これにより角度によって半径が変化します(なお、\(r(\theta)\)が単調増加(減少)関数である場合、曲線が「らせん」になります)。今回は、元の位置に戻ってくる「閉曲線」を考えたいので、関数\(r(\theta)\)には次のような条件が課されることになります。
①\(r(0)=r(2\pi)\).
②\(r(\theta)\)は連続.
①は始点と終点が同じ半径になるという条件ですが、これは比較的容易に調整できます。問題なのは②です。単純に\(r\)をランダムな値にすると、ギザギザの折れ線になってしまうので、緩やかなカーブを描くのにはどうすればいいか非常に悩みました。
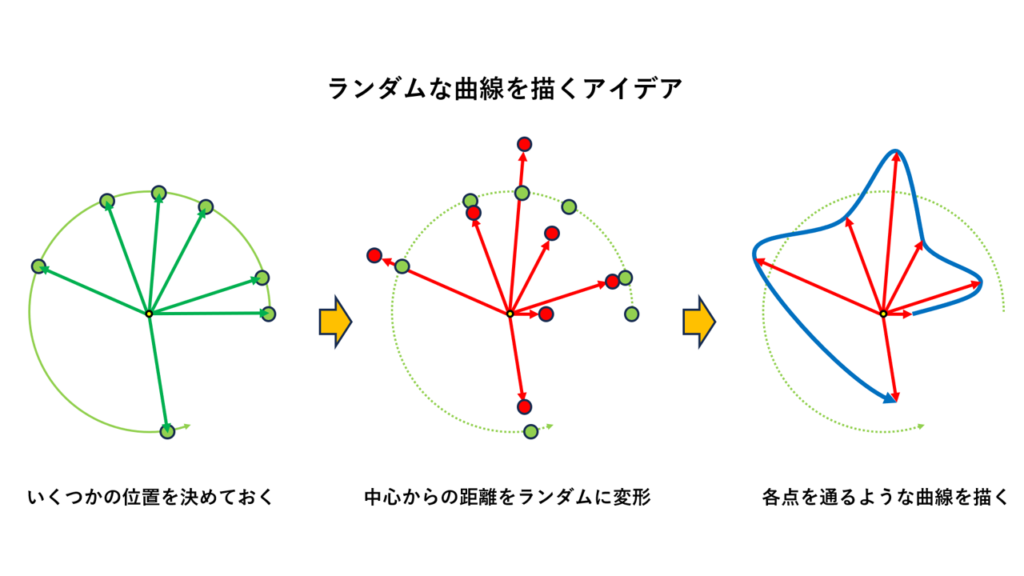
最初に思いついたのは、いくつかの点をランダムに配置し、それらの点を通るような多項式関数を作成するという方法です。これは「ラグランジュ補間」と呼ばれる手法で、機械的に構成することが可能です。しかし、これには決定的な弱点があり、始点と終点を無理やり一致させると、閉曲線として不自然な形になってしまうのです。
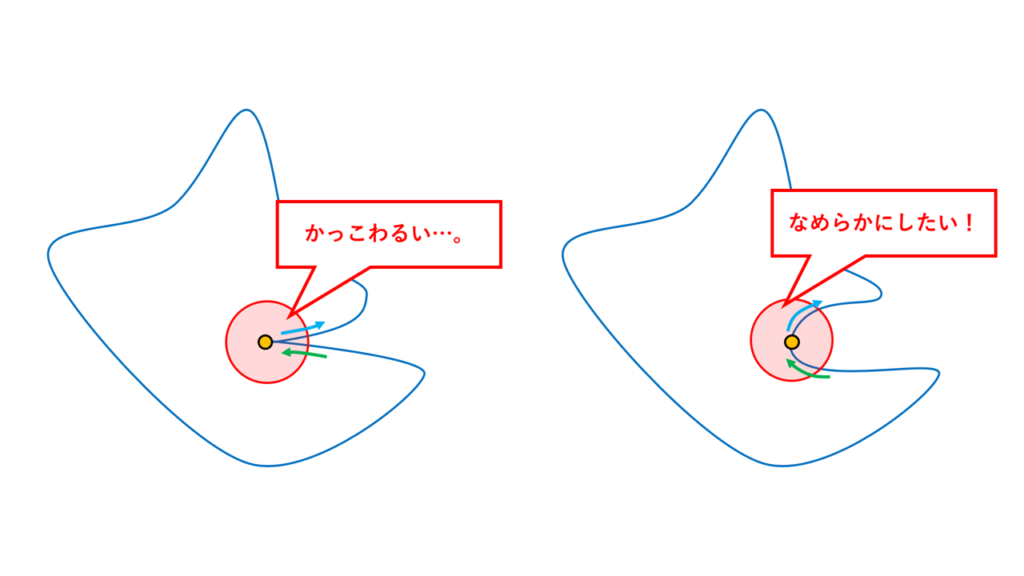
つまり、\(\theta=0,2\pi\)の位置でも緩やかにする必要があります。。。!この問題を解決するためにはある種の「周期性」を入れる必要があり、合同式(mod)を使用する方法も考えましたが、そもそもラグランジュ補間により、Excelの関数の式が長くなりすぎて、あまりエレガントな方法とは言えません(こういったところに美学があります)。そこでたどり着いたのが、「フーリエ展開」を用いた曲線の描写です。フーリエ展開とは簡単に言うと、「どんな周期的な関数も、波の式を重ねる(\(\sin\)や\(\cos\)の式を用いた無限和を用いる)ことで再現できる」というものです!これを利用することで、「ランダムでなめらかな周期関数」を生成することができ、これを\(r(\theta)\)とすれば、ランダムな閉曲線を作成することができます!実際に描いた結果がこちらです。
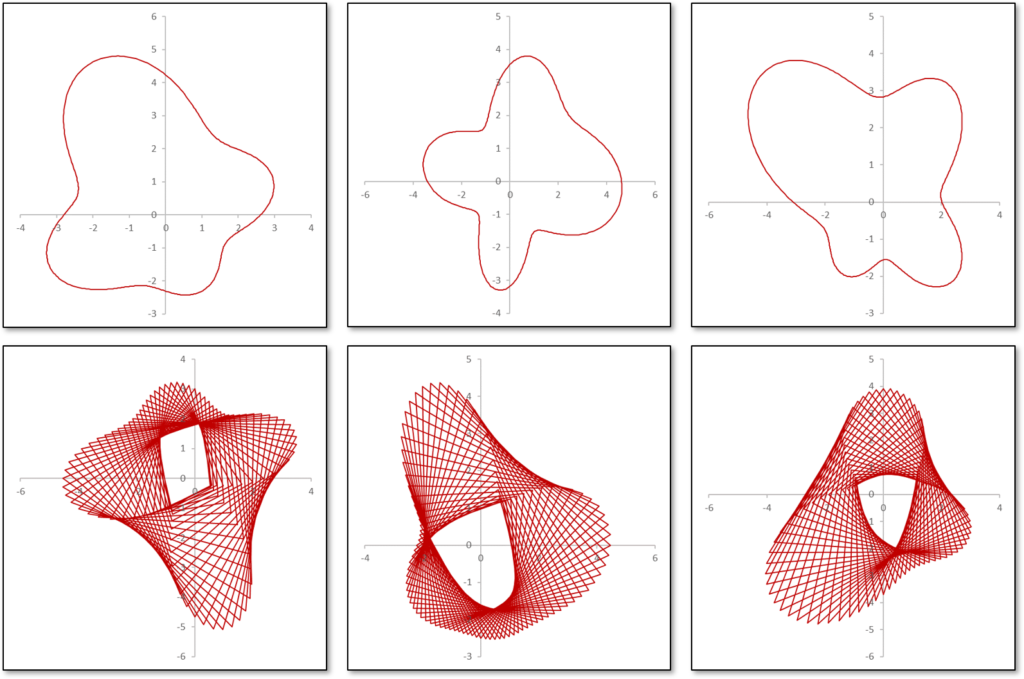
基本的にSIN関数とCOS関数を使って描いているので、角度の情報を細分化しておけば、なんと糸掛け曼荼羅を作成することも可能です!
3.さいごに
いかがでしたでしょうか?この「ランダム曲線」は糸掛け曼荼羅、参考文献は特にないですが、2024年1月24日に開催の「数学アートセミナー」にて、描き方や解説を行う予定です!完成されたExcelシートを配布いたしますので、興味のある方はぜひご参加ください。また、見逃してしまった方もご安心ください!セミナー実施後に録画した動画を配信いたします(1年間視聴可能です)。
↓詳しくはこちら!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>














