みなさんこんにちは！和からの数学講師の岡本です。久しぶりのマスログですが、今回も個人的に面白いなと思った内容を徒然なるままに書いていこうと思います！

今回の内容は「面白い曲線」です。数学では放物線や反比例、対数関数、三角関数など様々な曲線が現れます。どれも非常に面白い形をしていますが、どれも「学校の数学」な感じがして、人によっては苦手意識を感じる方もいらっしゃるかもしれません。

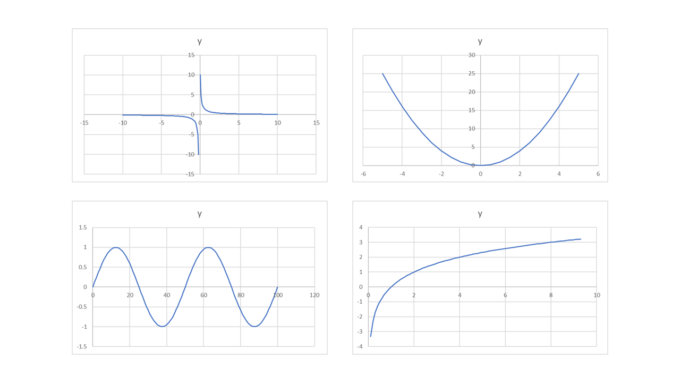
そこで、今回は単純に見て楽しめる、「面白い曲線」をご紹介しようと思います。

１．円とリサージュ曲線

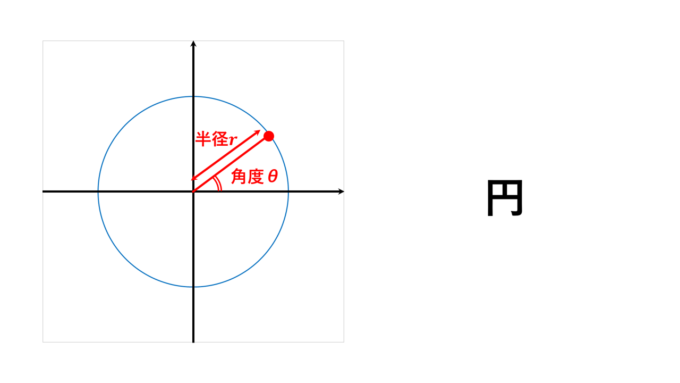
まず、小学校でもでてくる「円」という図形から入りましょう！中心から同じ距離だけ離れた点をつなぐことによってできる、シンプルで基本的な図形です。

半径$r$の円上の点$(x,y)$を表現するには三角関数を用いて

$$\begin{align*} (x,y)=(r\cos \theta, r\sin \theta) \end{align*}$$

と表すことができます。こうした$x, y$の座標を、それ以外の文字を使って表す方法を媒介変数表示といいます。このときの$\theta$を媒介変数と言います。このときに$\theta$は図のように$x$軸から半時計回りに回転した角度を表します。

さて、円の媒介変数表示を少し変形させると面白い模様になることをご存じでしょうか？たとえば、

$$\begin{align*} (x,y)=(r\cos 3\theta, r\sin 2\theta) \end{align*}$$

といった具合に、$x$成分の$\theta$を3倍、$y$成分の$\theta$を2倍としてみると次の図のような「面白い曲線」が描けます！

もちろん、3倍や2倍以外にもいろんな数字を入れても面白い曲線になります。

２．らせん

角度が変わるにつれて半径も変化していく曲線を考えます。つまり、半径$r$が$\theta$の関数となる場合を考えます。

$$\begin{align*} (x,y)=(r(\theta)\cos \theta, r(\theta)\sin \theta) \end{align*}$$

特に今回は単調に増加（あるいは減少）する関数を考えます。半径が単調に変化するような曲線を「らせん（螺線）」といいます（※「螺旋」は3次元の曲線のことなので、「螺線」とは異なります）。例えば、最も単純な例として$r(\theta)=\theta$の場合を考えてみましょう。

$$\begin{align*} (x,y)=(\theta\cos \theta, \theta\sin \theta) \end{align*}$$

この媒介変数表示で得られる曲線は以下の通りです。

このような蚊取り線香のような曲線を「アルキメデス螺線」といいます。また、$r(\theta)=(1.01)^{\theta}$といった具合に指数関数型にすると次のような螺線になります。

$$\begin{align*} (x,y)=(1.01^{\theta}\cos \theta, 1.01^{\theta}\sin \theta) \end{align*}$$

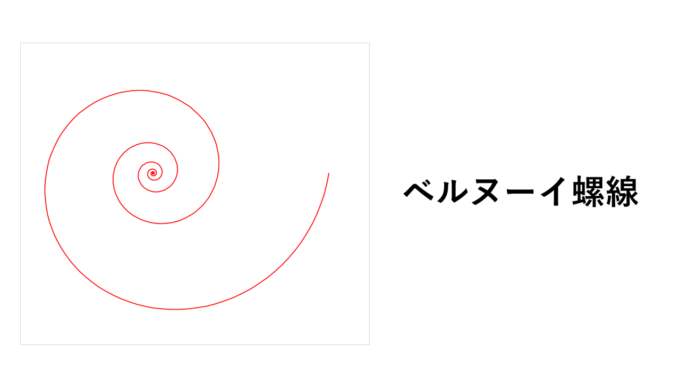
こうした貝殻のような螺線を「ベルヌーイ螺線」といいます。（数字の部分は1.01でなくても構いません。1.01を選んだ理由は、螺線の全体を見ていただくためです。ここの数が大きいと半径が急激に大きくなってしまい、うまく枠に収まりません。）

さらに、平方根を使って$r(\theta)=\sqrt{\theta}$と定めても、半径は単調に増加します。この場合、次のような螺線が出来上がります。

$$\begin{align*} (x,y)=(\sqrt{\theta}\cos \theta, \sqrt{\theta}\sin \theta) \end{align*}$$

線の間隔がだんだんと狭くなっていくという、面白い曲線になります。このタイプの螺線を「フェルマー螺線」といいます。

３．さいごに

いかがでしたでしょうか？このように、$\theta$や$r$を「いじくる」だけで面白い曲線を描くことができます。また円や今回紹介したリサージュ曲線のように元の位置に戻ってくる曲線と、螺線のように元の位置に戻ってこない曲線がありますが、基本的に興味がある（＝今後考察していく）のは元の位置に戻ってくる曲線です。その方がコンパクトですし、工夫もしやすくなります。次回は元の位置に戻ってくる曲線の例としてエピ/ハイポサイクロイド曲線を紹介していこうと思います。お楽しみに！！

今回の図は全てExcelを用いて作成しました！Excelを使ったアートに関しては無料講座を開催していますので、興味のある方は是非ご参加ください！

Excelアートセミナー

また、参考文献として岡本の拙著「アートで魅せる数学の世界」を挙げておきます。

アートで魅せる数学の世界 岡本健太郎 技術評論社
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>