【数学×アート】数式を使って「面白い曲線」を描きたい第2弾~円の周りをくるくると~

算数・物理・数学トピック

公開日

2023年4月23日

更新日

2023年4月23日

みなさんこんにちは！和からの数学講師の岡本です。今回も前回に引き続き、単純に見て楽しめる「面白い曲線」をご紹介しようと思います。前回の記事はこちらから！

【数学×アート】数式を使って「面白い曲線」を描きたい

この記事の主な内容

１．エピサイクロイドとハイポサイクロイド

円周上に印をつけた円を滑ることなく転がします。このときに印が描く軌跡を考えます。円を直線上に転がした場合にできる軌跡をサイクロイド(Cycloid)といいます。

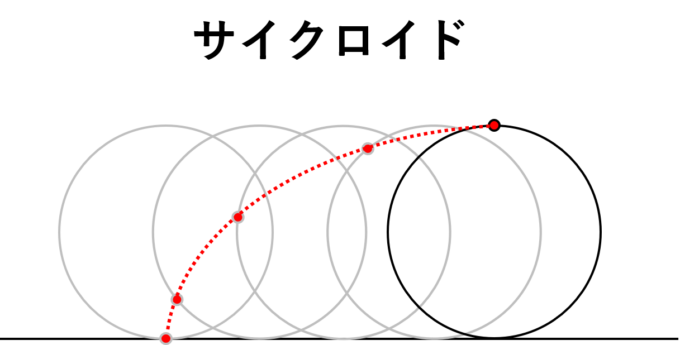
また、円を、より大きな円の外側を転がしてできる軌跡をエピサイクロイド(Epicycloid)、内側を転がしてできる軌跡をハイポサイクロイド(Hypocycloid)といいます。

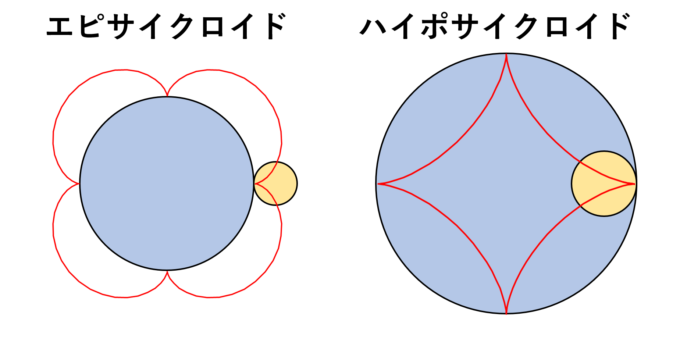
今回は、このエピサイクロイドとハイポサイクロイドがメインになってきます。転がる円の半径を\(r\),土台となる大きな円を\(R(>r)\),転がっている円の角度を\(\theta\)として、それぞれを式で表すと

・エピサイクロイド

\begin{align*}
(x,y)=((R+r)\cos \theta-r\cos \left(\frac{R+r}{r}\theta\right),(R+r)\sin \theta-r\sin \left(\frac{R+r}{r}\theta\right))
\end{align*}

・ハイポサイクロイド

\begin{align*}
(x,y)=((R-r)\cos \theta+r\cos \left(\frac{R-r}{r}\theta\right),(R-r)\sin \theta-r\sin \left(\frac{R-r}{r}\theta\right))
\end{align*}

と表すことができます。\(r\)や\(R\)の値を変えることによって曲線の形が変化して面白いです。なお、やっていくとわかってきますが、\(R\)が\(r\)の\(n(\geq3)\)倍であるとき、花びらがちょうど\(n\)枚となるようなシンプルな形になります。また、\(R\)と\(r\)が倍数の関係になっていないとき、エピ/ハイポサイクロイドは何周か回ってより複雑な曲線になります。

２．トロコイド

最初の節では、「円周上の点」の軌跡を考えました。次は「円内部の点」の軌跡を考えましょう。直線上でできる軌跡をトロコイド（Trochoid）といい、

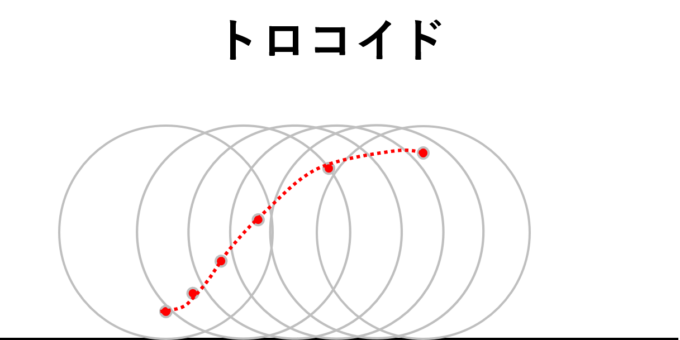
円の外側を転がす場合をエピトロコイド（Epitrochoid）、内側を転がす場合をハイポトロコイド（Hypotrochoid）といいます。サイクロイドよりも「柔らかな曲線」という印象です。

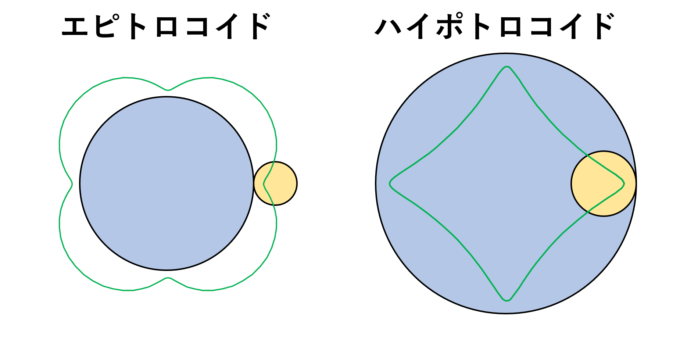
数式はそんなに複雑ではなく、エピ/ハイポサイクロイドを少しだけ変形すれば作成できます。「円内部の点」ということなので、エピ/ハイポサイクロイドの式の後半部分の半径\(r\)を、定数\(d\)を使って\(dr\)に変更すれば終わりです（\(d\)が0から1までの値のとき、「円の内部」を表現できます）。

・エピトロコイド

\begin{align*}
(x,y)=((R+r)\cos \theta-dr\cos \left(\frac{R+r}{r}\theta\right),(R+r)\sin \theta-dr\sin \left(\frac{R+r}{r}\theta\right))
\end{align*}

・ハイポトロコイド

\begin{align*}
(x,y)=((R-r)\cos \theta+dr\cos \left(\frac{R-r}{r}\theta\right),(R-r)\sin \theta-dr\sin \left(\frac{R-r}{r}\theta\right))
\end{align*}

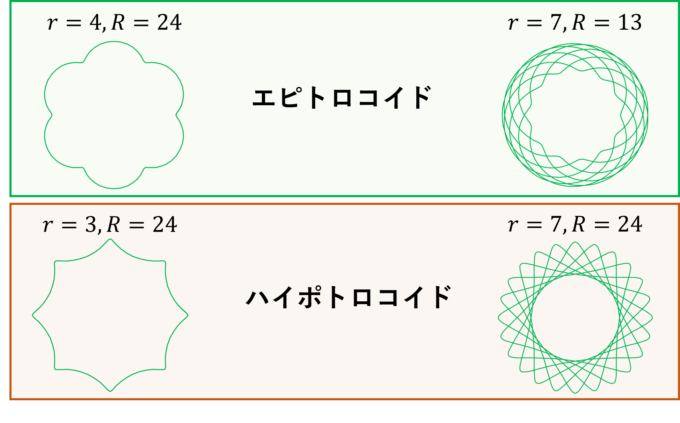
特にハイポトロコイドに関しては、教育用おもちゃとして広く知られている「スピログラフ」で描ける曲線と一致します。このあたりに関しては過去のマスログで少し解説しているので、こちらも併せてご覧ください。

Excelを使ったアートの世界～スピログラフ編～

３．さいごに

いかがでしたでしょうか？今回は円のまわりをくるくる回ってできる曲線について解説しました。この曲線の式をうまく応用することで、円だけではなく例えばリサージュ曲線の上を転がってできる軌跡も描けるようになります！次回は、より一般的な曲線（ランダムな曲線）を描くための考え方についてお話していきます。いよいよお伝えしたい内容に近づいてきました！次回もお楽しみに！

今回の図は全てExcelを用いて作成しました！Excelを使ったアートに関しては無料講座を開催していますので、興味のある方は是非ご参加ください！