やさしく学ぶ統計学~試行と事象とは?~
公開日
2023年4月19日
更新日
2023年4月19日

みなさんこんにちは。和からの数学講師の伊藤です。今回は、確率を考える際に必須となる試行と事象、そしてそれらの独立性、排反性に関するお話です。同じような概念であるため混乱してしまいがちですが、これらの概念を理解することで、より多くの場面での確率の計算ができるようになります。
この記事の主な内容
1. 試行、事象とは?
確率を考える際、サイコロを投げる、コインを投げるといった実験のことを試行と呼びます。また、試行をして観測された結果のことは事象と呼びます。これらの言葉はやや紛らわしいですが、例えばサイコロ投げの場合は、サイコロを投げるという実験そのものが試行であり、「1の目が出た」などの結果が事象となります。
事象の中には、いくつかの試行の結果を組み合わせてできるものもあります。例えばサイコロを3回投げる場合を考えると、{1, 5, 2}や{2, 2 , 2}のような事象が考えられます。
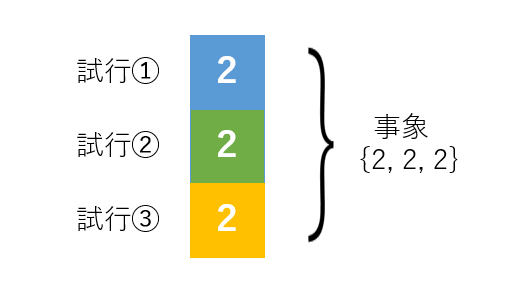
これらの概念における独立性、排反性を考えることで、確率の掛け算、足し算を正確に計算することができるようになります。
2. 試行の独立性
ここからは、独立、排反という2つの概念を紹介します。この2つも意味が似ているように思えますが、その違いを理解することは正確な計算を行う上で非常に重要です。
一連の試行で、ある試行の結果が他の試行の結果に影響を与えない場合、それぞれの試行が互いに独立であると言います。例えば、コイン投げやサイコロ投げを考えてみましょう。コイン投げでは、1回目に表が出る確率は、2回目に表が出る確率に影響を与えません。同様にサイコロ投げでは、1回目の出目は、2回目の出目に影響を与えないため、独立試行となります。
逆に、確率を考える際には、ある試行が他の試行に影響を与える場合もしばしば起こります。例えば、赤い玉と青い玉が2個ずつ入った袋から球を2回取り出す状況を考えてみましょう。この場合、1回目に赤い玉を引くと、袋の中身は赤い玉が1個、青い玉が2個となり、それぞれの玉を引く確率は1回目とは異なります。
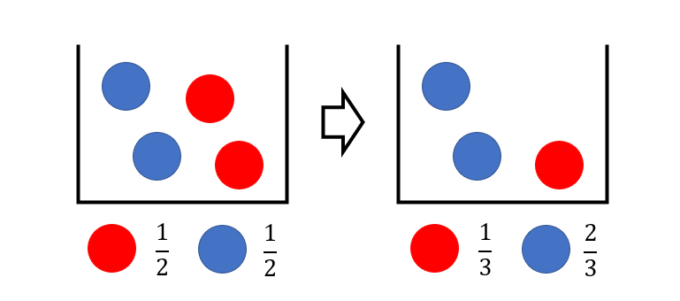
これは1回目の試行が2回目の試行に影響を与えているため、独立ではない試行となります。
3. 事象の独立性
試行だけではなく、事象にも独立性という考え方が存在します。2つの事象\(A\),\(B\)が独立であるとは、事象\(A\)の発生する確率に関わらず、事象\(B\)の発生する確率が変化しないことを言います。試行と事象の独立性を理解するために、次のようなゲームを考えましょう
これは、1回目にサイコロ投げ、2回目にコインを投げるという2つの試行からなりますが、これらの試行は独立ではありません。なぜなら、コイン投げの結果が表かどうかによって得点の計算方法が変わってくるため、コイン投げの結果がサイコロ投げの結果に影響しているためです。
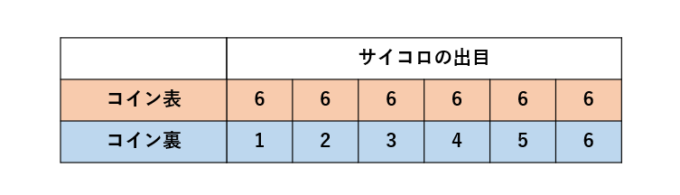
しかし、試行の結果生まれるそれぞれの事象の中には、独立なものが存在します。例えば、出目が奇数であるという事象\(A\)と、コインを投げて裏が出るという事象\(B\)を考えてみます。
コインを投げて裏が出る確率は\(1/2\)であり、サイコロを投げて出目が奇数である確率も\(1/2\)です。そして、サイコロの出目が奇数でありかつコイン投げで裏が出る確率は、次の表から\(1/4\)と分かります。

つまり、
\begin{align*}
P(A) \times P(B) = P(A \land B)
\end{align*}
という関係式が成り立っていることが分かります。この式は、事象\(B\)の発生が、事象\(A\)の発生確率に影響を与えていないということを意味します。この関係こそが、事象の独立性です。
では反対に、出目が奇数であるという事象\(A\)と、コイン投げの結果が裏であるという事象\(C\)を考えてみましょう。事象\(A\)が発生する確率は\(1/2\)、事象\(C\)が発生する確率も\(1/2\)です。では、事象\(A\)かつ\(C\)(サイコロの出目が奇数で、かつコインが裏)が発生する確率はというと、これは\(0\)になります。なぜならコインが裏だった時点で、サイコロの目が6と決まってしまうためです。この例は、\(P(A) \times P(B) = P(A \land B)\)が成り立たない例になっています。つまり、事象\(A\)と事象\(C\)は独立ではないことになるのです。
※この後排反な事象という言葉を紹介しますが、独立な試行から生まれる独立な事象であっても、それが排反になるとは限りません!
4. 排反な事象とは?
ある事象の発生が、他の事象の発生を排除する場合、それらを排反な事象と言います。これは言い換えると、2つの事象が同時に起こる確率\(0\)がである場合を指します。例としてコインを2回投げる場合を考えてみましょう。
コイン2回投げる際、「1回目に表が出る事象」と「2回とも裏が出る事象」は排反な事象です。1回目に表が出ると2回とも裏にはなりえないので、これらの事象が同時に発生することはあり得ません。
しかし、「1回目に表が出る事象」と「2回目に裏が出る事象」は排反ではありません。なぜなら、1回目が表であり、かつ2回目が裏であるような、被りがある事象が存在するためです。
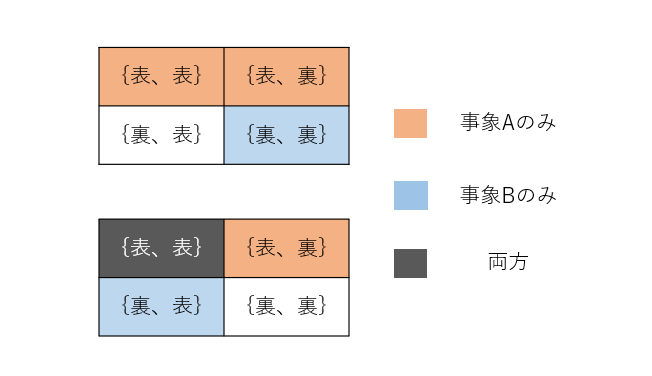
以上の独立試行・排反事象の考え方を持っておくと、確率計算の際に非常に重要となる確率の乗法定理、加法定理を理解するのに役立ちます!紛らわしい内容ではありますが、ぜひこういった独立性、排反性を正確に理解しておきましょう!
●和からのセミナー案内
Excelを用いたデータ分析のストーリーや可視化のスキルを学んでいくセミナーのご紹介です。興味を持っていただけた方は、ぜひ覗いてみてください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>














