ジョンソンの定理の美しさとその証明を味わおう！

公開日

2025年7月20日

更新日

2025年7月5日

こんにちは！和からの数学講師の岡本です。今回は、1916年にアメリカの数学者ロジャー・アーサー・ジョンソンによって証明された、美しい初等幾何の定理をご紹介します！

この記事の主な内容

１．ジョンソンの定理

まずは、ジョンソンの定理の主張を見てみましょう！

【ジョンソンの定理】
半径が等しい3つの円が1点で交わるとき、互いに交わる3つの交点を通る円は、3つの円と半径が等しい。

とてもシンプルながら驚きのある、美しい定理ですね！図を使って視覚的に確認してみましょう。

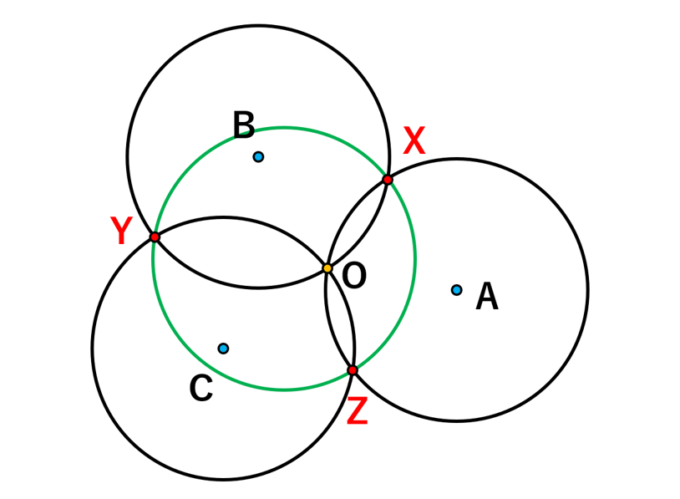
半径 \(R\) の3つの円の中心を \(A, B, C\)、3つの円が交わる点を \(O\)、各円同士の交点をそれぞれ \(X, Y, Z\) とします。このとき、三角形 \(XYZ\) の外接円の半径も \(R\) になる、というのがジョンソンの定理です。

２．ジョンソンの定理の証明（三角比を用いた幾何的手法）

それではこの定理を、三角比を使って高校数学レベルで証明してみましょう。

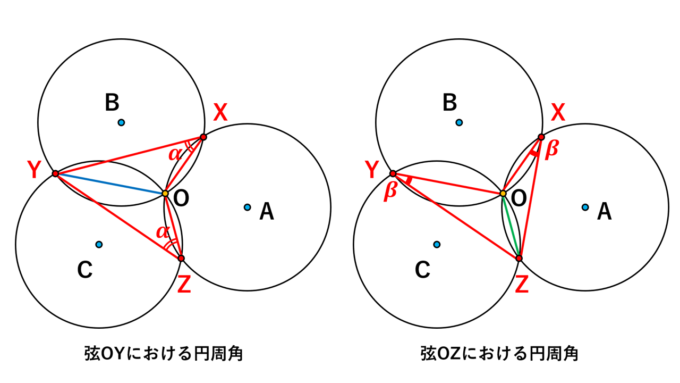
まず、円周角の性質に注目します。全ての円の半径が同じなので、同じ長さの弦に対する円周角は等しくなります。よって、

\begin{align*}
\angle OXY = \angle OZY = \alpha
\end{align*}

同様に、弦 \(OZ\) に対する円周角も等しくなり、

\begin{align*}
\angle OYZ = \angle OXZ = \beta
\end{align*}

と書けます。

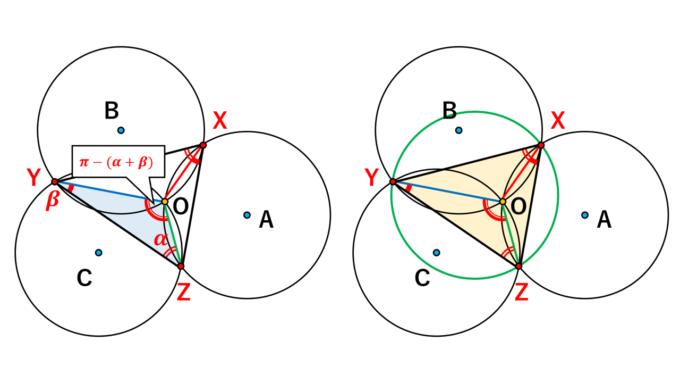
また、三角形 \(OYZ\) において内角の和は \(\pi\) なので、

\begin{align*}
\angle YOZ = \pi – (\alpha + \beta)
\end{align*}

となります。このとき、三角形 \(OYZ\) に正弦定理を適用すると：

\begin{align*}
2R = \frac{YZ}{\sin(\angle YOZ)} = \frac{YZ}{\sin(\pi-(\alpha + \beta))} = \frac{YZ}{\sin(\alpha + \beta)} = \frac{YZ}{\sin(\angle ZXY)}
\end{align*}

※ここで、\(\sin(\pi-x)=\sin x\)であることを利用しました。

したがって、三角形 \(XYZ\) の外接円の半径も \(R\) であることが示されました！

３．ジョンソンの定理の証明（ベクトルを用いた代数的手法）

今度は、ベクトルを用いてこの定理を代数的に証明してみましょう。

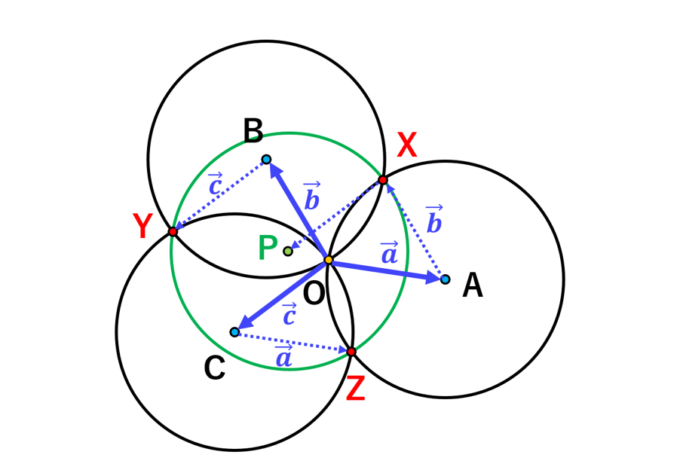
図のように、

\begin{align*}
\vec{a} = \vec{OA},　\quad \vec{b} = \vec{OB},　\quad \vec{c} = \vec{OC}
\end{align*}

と定めます。全ての円の半径が同じ \(R\) なので、

\begin{align*}
|\vec{a}| = |\vec{b}| = |\vec{c}| = R
\end{align*}

が成り立ちます。

このとき、円同士の交点である \(X, Y, Z\) に関して、

\begin{align*}
\vec{OX} = \vec{a} + \vec{b},\quad \vec{OY} = \vec{b} + \vec{c},\quad \vec{OZ} = \vec{c} + \vec{a}
\end{align*}

と表すことができます。

ここで、点 \(P\) を \(\vec{OP} = \vec{a} + \vec{b} + \vec{c}\) と定めると：

\begin{align*}
\vec{XP} = \vec{OP} – \vec{OX} = \vec{c},\quad \vec{YP} = \vec{OP} – \vec{OY} = \vec{a},\quad \vec{ZP} = \vec{OP} – \vec{OZ} = \vec{b}
\end{align*}

となり、各ベクトルの大きさは \(|\vec{XP}| = |\vec{YP}| = |\vec{ZP}| = R\) となるため、点 \(P\) は三角形 \(XYZ\) の外接円の中心であり、半径もやはり \(R\) であることがわかります。